matrix assignment solution

Definition, Formulas, Solved Example Problems - Solved Example Problems on Applications of Matrices: Solving System of Linear Equations | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants

Chapter: 12th mathematics : unit 1 : applications of matrices and determinants, solved example problems on applications of matrices: solving system of linear equations.

Solution to a System of Linear equations

(i) Matrix Inversion Method

Example 1.22.

Solve the following system of linear equations, using matrix inversion method:

5 x  +  2  y  =  3, 3 x  +  2  y  =  5 .

Then, applying the formula X = A −1 B , we get

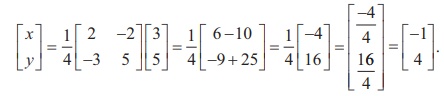
So the solution is ( x  = −1,  y  = 4).

Example 1.23

Solve the following system of equations, using matrix inversion method:

2 x 1  + 3 x 2  + 3 x 3  = 5,

x 1  – 2 x 2  +  x 3  = -4,

3 x 1  – x 2  – 2 x 3  = 3

The matrix form of the system is AX = B,where

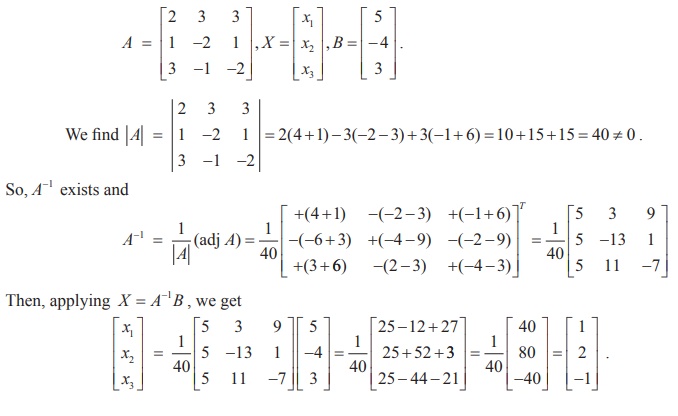
So, the solution is (  x 1  = 1,  x 2  = 2,  x 3  = −1) .

Example 1.24

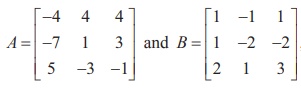
Writing the given system of equations in matrix form, we get

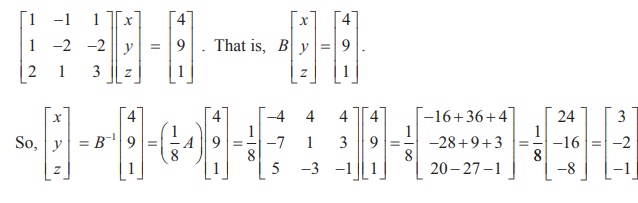
Hence, the solution is ( x  = 3,  y  = - 2,   z  = −1).

(ii) Cramer’s Rule

Example 1.25.

Solve, by Cramer’s rule, the system of equations

x 1   −   x 2   =  3, 2 x 1   +  3 x 2   +  4 x 3   =  17,  x 2   +  2 x 3   =  7.

First we evaluate the determinants

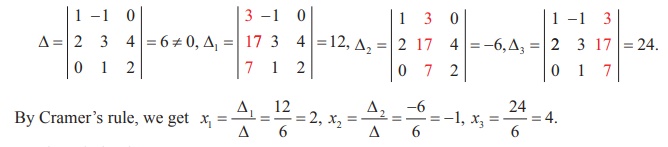
So, the solution is  ( x 1  = 2,  x 2  = - 1,   x 3  = 4).

Example 1.26

In a T20 match, Chennai Super Kings needed just 6 runs to win with 1 ball left to go in the last over. The last ball was bowled and the batsman at the crease hit it high up. The ball traversed along a path in a vertical plane and the equation of the path is  y  =   ax 2   +   bx  +   c  with respect to a  xy  -coordinate system in the  vertical  plane  and  the  ball  traversed   through   the   points  (10,8), (20,16), (30,18) , can you conclude that Chennai Super Kings won the  match?

Justify your answer. (All distances are measured in metres and the meeting point of the plane of  the path with the farthest boundary line is (70, 0).)

The path   y  =  ax 2  +  bx  +  c   passes through the points (10,8), (20,16), (40, 22) . So, we get   the   system   of   equations   100 a   + 10 b   +   c   =   8,   400 a   +   20 b   +   c =   16,1600 a   +   40 b   +   c   =   22.   To   apply   Cramer’s rule, we find

When  x  = 70, we get  y  = 6. 

So, the ball went by 6 metres high over the boundary line and it is impossible for a fielder  standing even just before theboundary line to jump and catch the ball.

    Hence the ball went for a super six and the Chennai Super Kings won the   match.

(iii) Gaussian Elimination Method

Example 1.27.

Solve the following system of linear equations, by Gaussian elimination method :

4 x  +  3 y  +  6 z  =  25,  x  +  5  y  +  7 z  =  13, 2 x  +  9  y  +   z  =  1.

Transforming the augmented matrix to echelon form, we get

The equivalent system is written by using the echelon form:

 x + 5y  + 7z = 13 , … (1)

 17y + 22z = 27 , … (2)

 199z = 398 . … (3)

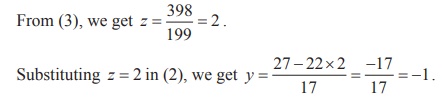
Substituting z = 2, y = -1  in (1), we get x = 13 - 5  × (−1 ) − 7 × 2 = 4 .

So, the solution is ( x =4, y = - 1, z = 2 ).

Note.  The above method of going from the last equation to the first equation is called the  method of back substitution .

Example 1.28

The  upward  speed   v ( t ) of a rocket  at time t is approximated by v(t) = at 2  + bt + c, 0 ≤  t ≤ 100 where a, b, and c are constants. It has been found that the speed at times t = 3, t = 6 , and t = 9 seconds are respectively, 64, 133, and 208 miles per second respectively. Find the speed at time  t = 15 seconds. (Use Gaussian elimination method.)

Since  v (3) =64,  v (6) = 133 and  v (9) = 208 , we get the following system of linear equations

 9a +3b + c = 64 ,

 36a + 6b + c = 133,

 81a + 9b + c = 208 .

We solve the above system of linear equations by Gaussian elimination method.

Reducing the augmented matrix to an equivalent row-echelon form by using elementary row  operations, we get

Writing the equivalent equations from the row-echelon matrix, we get

9a + 3b + c =  64, 2b + c = 41, c= 1.

By back substitution, we get 

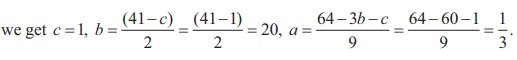
So, we get v (t) = 1/3 t 2    + 20t + 1.

Hence,  v (15) = 1/3 (225) + 20(15) + 1 = 75 + 300 + 1 = 376

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Index     Assignment problem     Hungarian algorithm     Solve online    

Solve an assignment problem online

Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given.

Fill in the cost matrix ( random cost matrix ):

Don't show the steps of the Hungarian algorithm Maximize the total cost

HungarianAlgorithm.com © 2013-2024

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

20S1 Matrix Assignment

Mathematics 2 (mh1811), nanyang technological university, recommended for you, students also viewed.

• MH1811 1516 S2 all - Test Doc
• MH1811 1213 S1 all - Test docs
• Past year papers of some thing
• MH1811 AY2020 2021 Sem 1 Test 1 18 Sep 2020 Answer
• MH1811 AY2020 2021 Sem 1 Test 1 18 Sep 2020

Related documents

• 12. 2019 H2 JC2 MSM Differential Equations (Solutions)
• MH1811 2017-2018 Semester 2
• MH1811 2017-2018 Semester 1
• MH1811 2016-2017 Semester 2
• MH1811 2016-2017 Semester 1
• MH1811 Cheatsheet full

Preview text

Matrix online assignment solution, school of physical and mathematical science, mh1810 mathematics i.

, then find AB.

[Solution:] We find

2(1) + 9(0) 2(1) + 9(1) 2(1) + 9(−1)

6(1) + 3(0) 6(1) + 3(1) 6(1) + 3(−1), ...............................................................................................................

• Suppose ABC + CBA is a 95 by 100 matrix. Then B is a by matrix.

[Solution:] Since ABC + CBA is a 95 by 100 matrix, both ABC and CBA are 95 by 100 matrices. This shows

that both A and C are 95 by 100 matrices. Since both ABC and CBA are defined, then B must be a 100 by 95

, then find A

[Solution:] We first find the determinant of A, that is

= 5(7) − 6(6) = − 1.

det(A) adj(

• Find the value k so that A =

is not invertible.

[Solution:] The matrix A is not invertible when det(A) = 0, hence the matrix A is not invertible when

det(A) = 0 ⇐⇒ k(1) − 7(3) = 0 ⇐⇒ k = 21.

• Find the determinant for the following matrix:

[Solution:] Note that the determinant of an upper triangular matrix is simply the product of its diagonal entries,

det(A) = 5 × 4 × 3 = 60.

• The following system of linear equations

{ 4 x + y = 4,

8 x + ky = 5,

has no solution. What is the value of k.

[Solution:] We write the system of linear equations can be written in the form of

For this case, we also have

det(A) = 0 ⇐⇒ The system has either no solution or infinitely many solutions.

det(A) = 0 ⇐⇒ 4 k − 8 = 0 ⇐⇒ k = 2.

But when k = 2, we have 4x+y = 4 and 8x+2y = 5 are different lines and parallel to each other (no intersection).

Hence, when k = 2, there is no solution.

• Find the value x if

3 x + 3 y = 0 ,

3 x − 3 z = 3 ,

x + y + z = 1.

[Solution:] We apply Cramer’s rule to find x, that is

Hence, we find

∣ ∣ ∣ ∣ ∣ ∣

[Solution:] We have {

1 + 6a + 4b = 1,

a + 6 + 4b = 36.

6 a + 4b = 0,

a + 4b = 30.

c = 6 + 4a + 3b = 9 and d = 6a + 4 + 3b = − 5.

• A water bottle full of melon juice weighs 723 grams and if it is half full, it weighs 482 grams. What is the weight

of the empty bottle?

[Solution:] Let m be the weight (in grams) of the melon juice when the bottle is full and b be the weight (in

grams) of the empty bottle. We have

{ b + m = 723

, where A =

Define Ab =

, then by Cramer’s Rule, we have

det(A) = 723

• Let A be a matrix that satisfies

Find det(A).

[Solution:] We have

Therefore, det(A) =

• Find the smallest positive k such that

[Solution:] Note that

( cos α − sin α

sin α cos α

cos β − sin β

sin β cos β

cos α cos β − sin α sin β − cos α sin β − sin α cos β

sin α cos β + cos α sin β − sin α sin β + cos α cos β

cos(α + β) − sin(α + β)

sin(α + β) cos(α + β)

Therefore, 

Hence, the smallest positive k is 12.

[Solution:] Note that,

−u if n is odd,

u if n is even.

537 u = −u =

• Let A be an invertible 4 by 4 matrix. Find det(

[Solution:] Note that, if A is an n by n matrix, then det(−A) = (−1)

n det(A). Also, since A is invertible,

det(A) 6 = 0. Therefore,

• Multiple Choice

Course : Mathematics 2 (MH1811)

University : nanyang technological university.

• More from: Mathematics 2 MH1811 Nanyang Technological University 136   Documents Go to course

• IIT JEE Study Material

Solving Linear Equations Using Matrix

Solving linear equations using matrix is done by two prominent methods, namely the matrix method and row reduction or the Gaussian elimination method. In this article, we will look at solving linear equations with matrix and related examples. With the study notes provided below, students will develop a clear idea about the topic.

Download Complete Chapter Notes of Matrices & Determinants Download Now

How to Solve Linear Equations Using Matrix Method?

Let the equations be:

The first method to find the solution to the system of equations is the matrix method. The steps to be followed are given below:

• All the variables in the equations should be written in the appropriate order.
• The variables, their coefficients and constants are to be written on the respective sides.

Solving a system of linear equations by the method of finding the inverse consists of two new matrices, namely

• Matrix A: which represents the variables
• Matrix B: which represents the constants

A system of equations can be solved using matrix multiplication.

We can write the above equations in the matrix form as follows:

Where, \(\begin{array}{l}A=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ {{c}_{1}} & {{c}_{2}} & {{c}_{3}} \\ \end{matrix} \right],\ X=\left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right],\ B=\left[ \begin{matrix} {{d}_{1}} \\ {{d}_{2}} \\ {{d}_{3}} \\ \end{matrix} \right]\end{array} \) .

A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.

The second method to find the solution for the system of equations is row reduction or Gaussian elimination.

• The augmented matrix for the linear equations is written.
• Use elementary such that all the elements below the main diagonal are zero. If a zero is obtained on the diagonal, perform the row operation such that a nonzero element is obtained.
• Back substitution is used to find the solution.

Related Topics:

• Introduction to Matrices
• Types of Matrices
• Matrix Operations
• Adjoint and Inverse of a Matrix
• Rank of a Matrix and Special Matrices

Solution to a System of Equations

A set of values of x, y, and z which simultaneously satisfy all the equations, is called a solution to the system of equations.

Consider, x + y + z = 9

2x – y + z = 5

4x + y – z = 7

Here, the set of values – x = 2, y = 3, z = 4, is a solution to the system of linear equations.

Because, 2 + 3 + 4 = 9, 4 – 3 + 4 = 5, 8 + 3 – 4 = 7

Consistent Equations

If the system of equations has one or more solutions, then it is said to be a consistent system of equations; otherwise, it is an inconsistent system of equations. For example, the system of linear equations x + 3y = 5;  x – y = 1 is consistent because x = 2, y = 1 is a solution to it. However, the system of linear equations x + 3y = 5; 2x + 6y = 8 is inconsistent because there is no set of values of x and y, which may satisfy the two equations simultaneously.

Condition for consistency of a system of linear equation AX = B

(b) If |A| = 0, and (Adj A) B ≠ 0, then the system is inconsistent.

(c) If |A| = 0, and (Adj A) B = 0, then the system is consistent and has infinitely many solutions.

Note AX = 0 is known as the homogeneous system of linear equations, and here, B = 0. A system of homogeneous equations is always consistent.

The system has a non-trivial solution (non-zero solution), if | A | = 0

Theorem 1: Let AX = B be a system of linear equations, where A is the coefficient matrix. If A is invertible, then the system has a unique solution, given by X = A -1 B

Uniqueness: If AX = B has two sets of solutions X 1 and X 2 , then AX 1 = B and AX 2 = B (Each equal to B).

⇒  AX 1 = AX 2

By cancellation law, A is invertible.

⇒  X 1 = X 2

Hence, the given system AX = B has a unique solution.

Note: A homogeneous system of equations is always consistent.

Problems on Solving Linear Equations Using Matrix Method

Illustration: Let A = \(\begin{array}{l}\left[ \begin{matrix} x+y & y \\ 2x & x-y \\ \end{matrix} \right],\ B=\left[ \begin{matrix} 2 \\ -1 \\ \end{matrix} \right],\ C = \left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]\end{array} \) . If AB = C, then find the matrix A 2 .

By solving AB = C, we get the values of x and y. Then by substituting these values in A, we obtain A 2

Here \(\begin{array}{l}\left[ \begin{matrix} x+y & y \\ 2x & x-y \\ \end{matrix} \right]\left[ \begin{matrix} 2 \\ -1 \\ \end{matrix} \right]=\left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]\\ \Rightarrow \left[ \begin{matrix} 2\left( x+y \right)-y \\ 2x.2-\left( x-y \right) \\ \end{matrix} \right]=\left[ \begin{matrix} 3 \\ 2 \\ \end{matrix} \right]\\ \Rightarrow 2\left( x+y \right)-y=3 \:\:and \:\:4x-\left( x-y \right)=2\end{array} \) \(\begin{array}{l}\Rightarrow \,\,2x+y=3\;\;\;\;and\;\;\;\;3x+y=2\end{array} \) Subtracting the two equations, we get, x = -1 So, y = 5 .

Illustration: Solve the following equations by matrix inversion

The given equation can be written in a matrix form as AX = D, and then by obtaining A -1 and multiplying it on both sides, we can solve the given problem.

then matrix A equals:

has no solution if a and b are

By applying row operation in the given matrices and comparing them, we can obtain the required result.

\(\begin{array}{l}\Rightarrow \,a=-3 \;\;and \;\;b\ne -1/3 \end{array} \) .

Applying \(\begin{array}{l}{{R}_{3}}\to {{R}_{3}}-2{{R}_{2}}+{{R}_{1}} \;\;and \;\;\;{{R}_{2}} to {{R}_{2}}-2{{R}_{1}}\end{array} \) we get;

Frequently Asked Questions

What do you mean by a linear equation.

A linear equation is an equation that has one or more variables having degree one.

Name two methods to solve linear equations using matrices.

The matrix multiplication method and the Gaussian elimination method are two methods to solve linear equations using matrices.

What do you mean by consistent equations?

A consistent system of equations is an equation having one or more solutions.

Give the formula used in the matrix multiplication method for solving linear equations.

We use the formula AX = B in the matrix multiplication method for solving linear equations. Here, A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.