hypothesis test for multiple regression

Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .

• Payment Plans
• Product List
• Partnerships

• Try Free Trial
• Study Packages
• Levels I, II & III Lifetime Package
• Video Lessons
• Study Notes
• Practice Questions
• Levels II & III Lifetime Package
• About the Exam
• About your Instructor
• Part I Study Packages
• Parts I & II Packages
• Part I & Part II Lifetime Package
• Part II Study Packages
• Exams P & FM Lifetime Package
• Quantitative Questions
• Verbal Questions
• Data Insight Questions
• Live Tutoring
• About your Instructors
• EA Practice Questions
• Data Sufficiency Questions
• Integrated Reasoning Questions

Hypothesis Tests and Confidence Intervals in Multiple Regression

After completing this reading you should be able to:

• Construct, apply, and interpret hypothesis tests and confidence intervals for a single coefficient in a multiple regression.
• Construct, apply, and interpret joint hypothesis tests and confidence intervals for multiple coefficients in a multiple regression.
• Interpret the \(F\)-statistic.
• Interpret tests of a single restriction involving multiple coefficients.
• Interpret confidence sets for multiple coefficients.
• Identify examples of omitted variable bias in multiple regressions.
• Interpret the \({ R }^{ 2 }\) and adjusted \({ R }^{ 2 }\) in a multiple regression.

Hypothesis Tests and Confidence Intervals for a Single Coefficient

This section is about the calculation of the standard error, hypotheses testing, and confidence interval construction for a single regression in a multiple regression equation.

Introduction

In a previous chapter, we looked at simple linear regression where we deal with just one regressor (independent variable). The response (dependent variable) is assumed to be affected by just one independent variable.  M ultiple regression, on the other hand ,  simultaneously considers the influence of multiple explanatory variables on a response variable Y. We may want to establish the confidence interval of one of the independent variables. We may want to evaluate whether any particular independent variable has a significant effect on the dependent variable. Finally, We may also want to establish whether the independent variables as a group have a significant effect on the dependent variable. In this chapter, we delve into ways all this can be achieved.

Hypothesis Tests for a single coefficient

Suppose that we are testing the hypothesis that the true coefficient \({ \beta }_{ j }\) on the \(j\)th regressor takes on some specific value \({ \beta }_{ j,0 }\). Let the alternative hypothesis be two-sided. Therefore, the following is the mathematical expression of the two hypotheses:

$$ { H }_{ 0 }:{ \beta }_{ j }={ \beta }_{ j,0 }\quad vs.\quad { H }_{ 1 }:{ \beta }_{ j }\neq { \beta }_{ j,0 } $$

This expression represents the two-sided alternative. The following are the steps to follow while testing the null hypothesis:

• Computing the coefficient’s standard error.

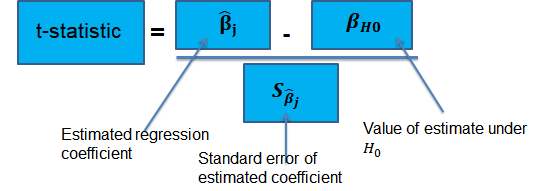
$$ p-value=2\Phi \left( -|{ t }^{ act }| \right) $$

• Also, the \(t\)-statistic can be compared to the critical value corresponding to the significance level that is desired for the test.

Confidence Intervals for a Single Coefficient

The confidence interval for a regression coefficient in multiple regression is calculated and interpreted the same way as it is in simple linear regression. 

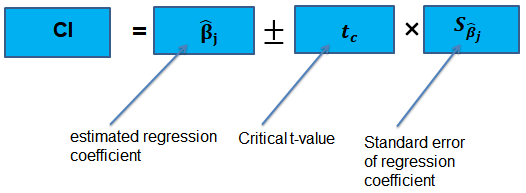
The t-statistic has n – k – 1 degrees of freedom where k = number of independents

Supposing that an interval contains the true value of \({ \beta }_{ j }\) with a probability of 95%. This is simply the 95% two-sided confidence interval for \({ \beta }_{ j }\). The implication here is that the true value of \({ \beta }_{ j }\) is contained in 95% of all possible randomly drawn variables.

Alternatively, the 95% two-sided confidence interval for \({ \beta }_{ j }\) is the set of values that are impossible to reject when a two-sided hypothesis test of 5% is applied. Therefore, with a large sample size:

$$ 95\%\quad confidence\quad interval\quad for\quad { \beta }_{ j }=\left[ { \hat { \beta } }_{ j }-1.96SE\left( { \hat { \beta } }_{ j } \right) ,{ \hat { \beta } }_{ j }+1.96SE\left( { \hat { \beta } }_{ j } \right) \right] $$

Tests of Joint Hypotheses

In this section, we consider the formulation of the joint hypotheses on multiple regression coefficients. We will further study the application of an \(F\)-statistic in their testing.

Hypotheses Testing on Two or More Coefficients

Joint null hypothesis.

In multiple regression, we canno t test the null hypothesis that all slope coefficients are equal 0 based on t -tests that each individual slope coefficient equals 0. Why? individual t-tests do not account for the effects of interactions among the independent variables.

For this reason, we conduct the F-test which uses the F-statistic .  The F-test tests the null hypothesis that all of the slope coefficients in the multiple regression model are jointly equal to 0, .i.e.,

\(F\)-Statistic

The F-statistic, which is always a one-tailed test , is calculated as:

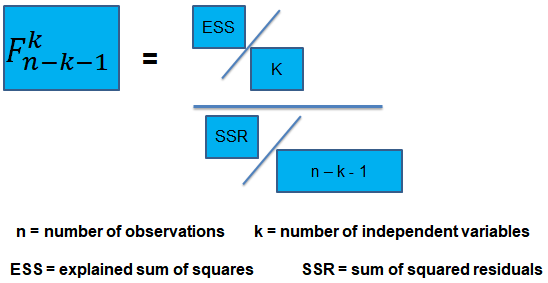
To determine whether at least one of the coefficients is statistically significant, the calculated F-statistic is compared with the one-tailed critical F-value, at the appropriate level of significance.

Decision rule:

Rejection of the null hypothesis at a stated level of significance indicates that at least one of the coefficients is significantly different than zero, i.e, at least one of the independent variables in the regression model makes a significant contribution to the dependent variable.

An analyst runs a regression of monthly value-stock returns on four independent variables over 48 months.

The total sum of squares for the regression is 360, and the sum of squared errors is 120.

Test the null hypothesis at the 5% significance level (95% confidence) that all the four independent variables are equal to zero.

\({ H }_{ 0 }:{ \beta }_{ 1 }=0,{ \beta }_{ 2 }=0,\dots ,{ \beta }_{ 4 }=0 \)

\({ H }_{ 1 }:{ \beta }_{ j }\neq 0\) (at least one j is not equal to zero, j=1,2… k )

ESS = TSS – SSR = 360 – 120 = 240

The calculated test statistic = (ESS/k)/(SSR/(n-k-1))

=(240/4)/(120/43) = 21.5

\({ F }_{ 43 }^{ 4 }\) is approximately 2.44 at 5% significance level.

Decision: Reject H 0 .

Conclusion: at least one of the 4 independents is significantly different than zero.

Omitted Variable Bias in Multiple Regression

This is the bias in the OLS estimator arising when at least one included regressor gets collaborated with an omitted variable. The following conditions must be satisfied for an omitted variable bias to occur:

• There must be a correlation between at least one of the included regressors and the omitted variable.
• The dependent variable \(Y\) must be determined by the omitted variable.

Practical Interpretation of the \({ R }^{ 2 }\) and the adjusted \({ R }^{ 2 }\), \({ \bar { R } }^{ 2 }\)

To determine the accuracy within which the OLS regression line fits the data, we apply the coefficient of determination and the regression’s standard error . 

The coefficient of determination, represented by \({ R }^{ 2 }\), is a measure of the “goodness of fit” of the regression. It is interpreted as the percentage of variation in the dependent variable explained by the independent variables

\({ R }^{ 2 }\) is not a reliable indicator of the explanatory power of a multiple regression model.Why? \({ R }^{ 2 }\) almost always increases as new independent variables are added to the model, even if the marginal contribution of the new variable is not statistically significant. Thus, a high \({ R }^{ 2 }\) may reflect the impact of a large set of independents rather than how well the set explains the dependent.This problem is solved by the use of the adjusted \({ R }^{ 2 }\) (extensively covered in chapter 8)

The following are the factors to watch out when guarding against applying the \({ R }^{ 2 }\) or the \({ \bar { R } }^{ 2 }\):

• An added variable doesn’t have to be statistically significant just because the \({ R }^{ 2 }\) or the \({ \bar { R } }^{ 2 }\) has increased.
• It is not always true that the regressors are a true cause of the dependent variable, just because there is a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
• It is not necessary that there is no omitted variable bias just because we have a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
• It is not necessarily true that we have the most appropriate set of regressors just because we have a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
• It is not necessarily true that we have an inappropriate set of regressors just because we have a low \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).

An economist tests the hypothesis that GDP growth in a certain country can be explained by interest rates and inflation.

Using some 30 observations, the analyst formulates the following regression equation:

$$ GDP growth = { \hat { \beta } }_{ 0 } + { \hat { \beta } }_{ 1 } Interest+ { \hat { \beta } }_{ 2 } Inflation $$

Regression estimates are as follows:

Is the coefficient for interest rates significant at 5%?

• Since the test statistic < t-critical, we accept H 0 ; the interest rate coefficient is  not   significant at the 5% level.
• Since the test statistic > t-critical, we reject H 0 ; the interest rate coefficient is not significant at the 5% level.
• Since the test statistic > t-critical, we reject H 0 ; the interest rate coefficient is significant at the 5% level.
• Since the test statistic < t-critical, we accept H 1 ; the interest rate coefficient is significant at the 5% level.

The correct answer is  C .

We have GDP growth = 0.10 + 0.20(Int) + 0.15(Inf)

Hypothesis:

$$ { H }_{ 0 }:{ \hat { \beta } }_{ 1 } = 0 \quad vs \quad { H }_{ 1 }:{ \hat { \beta } }_{ 1 }≠0 $$

The test statistic is:

$$ t = \left( \frac { 0.20 – 0 }{ 0.05 } \right)  = 4 $$

The critical value is t (α/2, n-k-1) = t 0.025,27  = 2.052 (which can be found on the t-table).

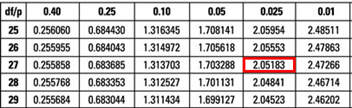
Conclusion : The interest rate coefficient is significant at the 5% level.

Offered by AnalystPrep

Modeling Cycles: MA, AR, and ARMA Models

Empirical approaches to risk metrics and hedging, linear regression.

After completing this reading, you should be able to: Describe the models that... Read More

Deciphering the Liquidity and Credit C ...

After completing this reading, you should be able to: Describe the key factors... Read More

Foreign Exchange Risk

After completing this reading, you should be able to: Calculate a financial institution’s... Read More

Multivariate Random Variables

After completing this reading, you should be able to: Explain how a probability... Read More

Leave a Comment Cancel reply

You must be logged in to post a comment.

• 5.7 - MLR Parameter Tests

Earlier in this lesson, we translated three different research questions pertaining to the heart attacks in rabbits study ( coolhearts.txt ) into three sets of hypotheses we can test using the general linear F -statistic. The research questions and their corresponding hypotheses are:

1. Is the regression model containing at least one predictor useful in predicting the size of the infarct?

• H 0 : β 1 = β 2 = β 3 = 0
• H A : At least one β j ≠ 0 (for j = 1, 2, 3)

2. Is the size of the infarct significantly (linearly) related to the area of the region at risk?

• H 0 : β 1 = 0
• H A : β 1 ≠ 0

3. (Primary research question) Is the size of the infarct area significantly (linearly) related to the type of treatment upon controlling for the size of the region at risk for infarction?

• H 0 : β 2 = β 3 = 0
• H A : At least one β j ≠ 0 (for j = 2, 3)

Let's test each of the hypotheses now using the general linear F -statistic:

\[F^*=\left(\frac{SSE(R)-SSE(F)}{df_R-df_F}\right) \div \left(\frac{SSE(F)}{df_F}\right)\]

To calculate the F -statistic for each test, we first determine the error sum of squares for the reduced and full models — SSE ( R ) and SSE ( F ), respectively. The number of error degrees of freedom associated with the reduced and full models — df R and df F , respectively — is the number of observations, n , minus the number of parameters, k +1 , in the model. That is, in general, the number of error degrees of freedom is n – ( k +1) . We use statistical software to determine the P -value for each test.

Testing all slope parameters equal 0

To answer the research question: "Is the regression model containing at least one predictor useful in predicting the size of the infarct?," we test the hypotheses:

The full model. The full model is the largest possible model — that is, the model containing all of the possible predictors. In this case, the full model is:

\[y_i=(\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i3})+\epsilon_i\]

The error sum of squares for the full model, SSE ( F ), is just the usual error sum of squares, SSE , that appears in the analysis of variance table. Because there are k +1 = 3+1 = 4 parameters in the full model, the number of error degrees of freedom associated with the full model is df F = n – 4.

The reduced model. The reduced model is the model that the null hypothesis describes. Because the null hypothesis sets each of the slope parameters in the full model equal to 0, the reduced model is:

\[y_i=\beta_0+\epsilon_i\]

The reduced model basically suggests that none of the variation in the response y is explained by any of the predictors. Therefore, the error sum of squares for the reduced model, SSE ( R ), is just the total sum of squares, SSTO , that appears in the analysis of variance table. Because there is only one parameter in the reduced model, the number of error degrees of freedom associated with the reduced model is df R = n – 1.

The test. Upon plugging in the above quantities, the general linear F -statistic:

\[F^*=\frac{SSE(R)-SSE(F)}{df_R-df_F} \div \frac{SSE(F)}{df_F}\]

becomes the usual " overall F -test ":

\[F^*=\frac{SSR}{3} \div \frac{SSE}{n-4}=\frac{MSR}{MSE}.\]

That is, to test H 0 : β 1 = β 2 = β 3 = 0, we just use the overall F -test and P -value reported in the analysis of variance table:

\[F^*=\frac{0.95927}{3} \div \frac{0.54491}{28}=\frac{0.31976}{0.01946}=16.43.\]

There is sufficient evidence ( F = 16.43, P < 0.001) to conclude that at least one of the slope parameters is not equal to 0.

In general, to test that all of the slope parameters in a multiple linear regression model are 0, we use the overall F -test reported in the analysis of variance table.

Testing one slope parameter is 0

Now let's answer the second research question: "Is the size of the infarct significantly (linearly) related to the area of the region at risk?" To do so, we test the hypotheses:

The full model. Again, the full model is the model containing all of the possible predictors:

The error sum of squares for the full model, SSE ( F ), is just the usual error sum of squares, SSE . Alternatively, because the three predictors in the model are x 1 , x 2 , and x 3 , we can denote the error sum of squares as SSE ( x 1 , x 2 , x 3 ). Again, because there are 4 parameters in the model, the number of error degrees of freedom associated with the full model is df F = n – 4.

The reduced model. Because the null hypothesis sets the first slope parameter, β 1 , equal to 0, the reduced model is:

\[y_i=(\beta_0+\beta_2x_{i2}+\beta_3x_{i3})+\epsilon_i\]

Because the two predictors in the model are x 2 and x 3 , we denote the error sum of squares as SSE ( x 2 , x 3 ). Because there are 3 parameters in the model, the number of error degrees of freedom associated with the reduced model is df R = n – 3.

The test. The general linear statistic:

simplifies to:

\[F^*=\frac{SSR(x_1|x_2, x_3)}{1}\div \frac{SSE(x_1,x_2, x_3)}{n-4}=\frac{MSR(x_1|x_2, x_3)}{MSE(x_1,x_2, x_3)}\]

Getting the numbers from the following output:

we determine that value of the F -statistic is:

\[F^*=\frac{SSR(x_1|x_2, x_3)}{1}\div MSE=\frac{0.63742}{0.01946}=32.7554.\]

The P -value is the probability — if the null hypothesis were true — that we would get an F -statistic larger than 32.7554. Comparing our F -statistic to an F -distribution with 1 numerator degree of freedom and 28 denominator degrees of freedom, the probability is close to 1 that we would observe an F -statistic smaller than 32.7554:

Therefore, the probability that we would get an F -statistic larger than 32.7554 is close to 0. That is, the P -value is < 0.001. There is sufficient evidence ( F = 32.8, P < 0.001) to conclude that the size of the infarct is significantly related to the size of the area at risk.

But wait a second! Have you been wondering why we couldn't just use the slope's t -statistic to test that the slope parameter, β 1 , is 0? We can! Notice that the P -value ( P < 0.001) for the t -test ( t * = 5.72):

is the same as the P -value we obtained for the F -test. This will be always be the case when we test that only one slope parameter is 0. That's because of the well-known relationship between a t -statistic and an F -statistic that has one numerator degree of freedom:

\[t_{(n-(k+1))}^{2}=F_{(1, n-(k+1))}\]

For our example, the square of the t -statistic, 5.72, equals our F -statistic (within rounding error). That is:

\[t^{*2}=5.72^2=32.72=F^*\]

So what have we learned in all of this discussion about the equivalence of the F -test when testing only one slope parameter and the t -test? In short:

• We can use either the F -test or the t -test to test that only one slope parameter is 0. Because the t -test results can be read directly from the software output, it makes sense that it would be the test that we'll use most often.
• But, we have to be careful with our interpretations! The equivalence of the t -test to the F -test when testing only one slope parameter has taught us something new about the t -test. The t -test is a test for the marginal significance of the x 1 predictor after the other predictors x 2 and x 3 have been taken into account. It does not test for the significance of the relationship between the response y and the predictor x 1 alone.

Testing a subset of slope parameters is 0

Finally, let's answer the third — and primary — research question: "Is the size of the infarct area significantly (linearly) related to the type of treatment upon controlling for the size of the region at risk for infarction?" To do so, we test the hypotheses:

The error sum of squares for the full model, SSE ( F ), is just the usual error sum of squares, SSE = 0.54491 from the output above. Alternatively, because the three predictors in the model are x 1 , x 2 , and x 3 , we can denote the error sum of squares as SSE ( x 1 , x 2 , x 3 ). Again, because there are 4 parameters in the model, the number of error degrees of freedom associated with the full model is df F = n – 4 = 32 – 4 = 28.

The reduced model. Because the null hypothesis sets the second and third slope parameters, β 2 and β 3 , equal to 0, the reduced model is:

\[y_i=(\beta_0+\beta_1x_{i1})+\epsilon_i\]

The ANOVA table for the reduced model is:

Because the only predictor in the model is x 1 , we denote the error sum of squares as SSE ( x 1 ) = 0.8793. Because there are 2 parameters in the model, the number of error degrees of freedom associated with the reduced model is df R = n – 2 = 32 – 2 = 30.

The test. The general linear statistic is:

\[F^*=\frac{SSE(R)-SSE(F)}{df_R-df_F} \div\frac{SSE(F)}{df_F}=\frac{0.8793-0.54491}{30-28} \div\frac{0.54491}{28}= \frac{0.33439}{2} \div 0.01946=8.59.\]

The P -value is the probability — if the null hypothesis were true — that we would observe an F -statistic more extreme than 8.59. The following output:

tells us that the probability of observing such an F -statistic that is smaller than 8.59 is 0.9988. Therefore, the probability of observing such an F -statistic that is larger than 8.59 is 1 – 0.9988 = 0.0012. The P -value is very small. There is sufficient evidence ( F = 8.59, P = 0.0012) to conclude that the type of cooling is significantly related to the extent of damage that occurs — after taking into account the size of the region at risk.

Summary of MLR Testing

For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are:

• Hypothesis test for testing that all of the slope parameters are 0.
• Hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0.
• Hypothesis test for testing that one slope parameter is 0.

We have learned how to perform each of the above three hypothesis tests.

The F -statistic and associated p -value in the ANOVA table are used for testing whether all of the slope parameters are 0. In most applications this p -value will be small enough to reject the null hypothesis and conclude that at least one predictor is useful in the model. For example, for the rabbit heart attacks study, the F -statistic is (0.95927/3) / (0.54491/(32–4)) = 16.43 with p -value 0.000.

To test whether a subset — more than one, but not all — of the slope parameters are 0, u se the general linear F-test formula by fitting the full model to find SSE(F) and fitting the reduced model to find SSE(R) . Then the numerator of the F-statistic is (SSE(R) – SSE(F)) / (df R – df F ) .  The denominator of the F -statistic is the mean squared error in the ANOVA table.  For example, for the rabbit heart attacks study, the general linear F-statistic is [(0.8793 – 0.54491) / (30 – 28)] / (0.54491 / 28) = 8.59 with p -value 0.0012.

To test whether one slope parameter is 0, we can use an F -test as just described. Alternatively, we can use a t -test, which will have an identical p -value since in this case the square of the t -statistic is equal to the F -statistic. For example, for the rabbit heart attacks study, the F -statistic for testing the slope parameter for the Area predictor is (0.63742/1) / (0.54491/(32–4)) = 32.75 with p -value 0.000. Alternatively, the t -statistic for testing the slope parameter for the Area predictor is 0.613 / 0.107 = 5.72 with p -value 0.000, and 5.72 2 = 32.72.

Incidentally, you may be wondering why we can't just do a series of individual t-tests to test whether a subset of the slope parameters are 0. For example, for the rabbit heart attacks study, we could have done the following:

• Fit the model of y = InfSize on x 1 = Area and x 2 and x 3 and use an individual t-test for x 3 .
• If the test results indicate that we can drop x 3 then fit the model of y = InfSize on x 1 = Area and x 2 and use an individual t-test for x 2 .

The problem with this approach is we're using two individual t-tests instead of one F-test, which means our chance of drawing an incorrect conclusion in our testing procedure is higher. Every time we do a hypothesis test, we can draw an incorrect conclucion by:

• rejecting a true null hypothesis, i.e., make a type 1 error by concluding the tested predictor(s) should be retained in the model, when in truth it/they should be dropped; or
• failing to reject a false null hypothesis, i.e., make a type 2 error by concluding the tested predictor(s) should be dropped from the model, when in truth it/they should be retained.

Thus, in general, the fewer tests we perform the better. In this case, this means that wherever possible using one F-test in place of multiple individual t-tests is preferable. 

The plot shows a similar positive linear trend within each treatment category, which suggests that it is reasonable to formulate a multiple regression model that would place three parallel lines through the data.

Minitab creates an indicator variable for each treatment group but we can only use two, for treatment groups 1 and 2 in this case (treatment group 3 is the reference level in this case).

The fitted equation from Minitab is Yield = 84.99 + 1.3088 Nit - 2.43 x 2 - 2.35 x 3 , which means that the equations for each treatment group are:

Group 1: Yield = 84.99 + 1.3088 Nit - 2.43(1) = 82.56 + 1.3088 Nit Group 2: Yield = 84.99 + 1.3088 Nit - 2.35(1) = 82.64 + 1.3088 Nit Group 3: Yield = 84.99 + 1.3088 Nit

The three estimated regression lines are parallel since they have the same slope, 1.3088.

The regression parameter for x 2 represents the difference between the estimated intercept for treatment 1 and the estimated intercept for the reference treatment 3.

The regression parameter for x 3 represents the difference between the estimated intercept for treatment 2 and the estimated intercept for the reference treatment 3.

\(H_0 : \beta_1=\beta_2=\beta_3 = 0\) against the alternative \(H_A\) : at least one of the \(\beta_i\) is not 0.

\(F = (16039.5/3) / (1078.0/(30-4)) = 5346.5 / 41.46 = 128.95\).

Since the p -value for this F -statistic is reported as 0.000, we reject H 0 in favor of H A and conclude that at least one of the slope parameters is not zero, i.e., the regression model containing at least one predictor is useful in predicting the size of sugar beet yield.

\(H_0:\beta_1= 0\) against the alternative \(H_A:\beta_1 \ne 0\)

t -statistic = 19.60, p -value = 0.000, so we reject H 0 in favor of H A and conclude that the slope parameter for x 1 = nit is not zero, i.e., sugar beet yield is significantly linearly related to the available nitrogen (controlling for treatment).

F -statistic \(= (15934.5/1) / (1078.0/(30-4)) = 15934.5 / 41.46 = 384.32\), which is the same as 19.60 2 .

\(H_0:\beta_2=\beta_3= 0\) against the alternative \(H_A:\beta_2 \ne 0\) or \(\beta_3 \ne 0\) or both \(\ne 0\).

\(F = ((10.4+27.5)/2) / (1078.0/(30-4)) = 18.95 / 41.46 = 0.46\).

F distribution with 2 DF in numerator and 26 DF in denominator    x  P( X ≤ x ) 0.46    0.363677

p -value \(= 1-0.363677 = 0.636\), so we fail to reject H 0 in favor of H A and conclude that we cannot rule out \(\beta_2 = \beta_3 = 0\), i.e., there is no significant difference in the mean yields of sugar beets subjected to the different growth regulators after taking into account the available nitrogen.

Start Here!

• Welcome to STAT 462!
• Search Course Materials
• Lesson 1: Statistical Inference Foundations
• Lesson 2: Simple Linear Regression (SLR) Model
• Lesson 3: SLR Evaluation
• Lesson 4: SLR Assumptions, Estimation & Prediction
• 5.1 - Example on IQ and Physical Characteristics
• 5.2 - Example on Underground Air Quality
• 5.3 - The Multiple Linear Regression Model
• 5.4 - A Matrix Formulation of the Multiple Regression Model
• 5.5 - Three Types of MLR Parameter Tests
• 5.6 - The General Linear F-Test
• 5.8 - Partial R-squared
• 5.9- Further MLR Examples
• Lesson 6: MLR Assumptions, Estimation & Prediction
• Lesson 7: Transformations & Interactions
• Lesson 8: Categorical Predictors
• Lesson 9: Influential Points
• Lesson 10: Regression Pitfalls
• Lesson 11: Model Building
• Lesson 12: Logistic, Poisson & Nonlinear Regression
• Website for Applied Regression Modeling, 2nd edition
• Notation Used in this Course
• R Software Help
• Minitab Software Help

Copyright © 2018 The Pennsylvania State University Privacy and Legal Statements Contact the Department of Statistics Online Programs

Applied Data Science Meeting, July 4-6, 2023, Shanghai, China . Register for the workshops: (1) Deep Learning Using R, (2) Introduction to Social Network Analysis, (3) From Latent Class Model to Latent Transition Model Using Mplus, (4) Longitudinal Data Analysis, and (5) Practical Mediation Analysis. Click here for more information .

• Example Datasets
• Basics of R
• Graphs in R

Hypothesis testing

• Confidence interval
• Simple Regression
• Multiple Regression
• Logistic regression
• Moderation analysis
• Mediation analysis
• Path analysis
• Factor analysis
• Multilevel regression
• Longitudinal data analysis
• Power analysis

Multiple Linear Regression

The general purpose of multiple regression (the term was first used by Pearson, 1908), as a generalization of simple linear regression, is to learn about how several independent variables or predictors (IVs) together predict a dependent variable (DV). Multiple regression analysis often focuses on understanding (1) how much variance in a DV a set of IVs explain and (2) the relative predictive importance of IVs in predicting a DV.

In the social and natural sciences, multiple regression analysis is very widely used in research. Multiple regression allows a researcher to ask (and hopefully answer) the general question "what is the best predictor of ...". For example, educational researchers might want to learn what the best predictors of success in college are. Psychologists may want to determine which personality dimensions best predicts social adjustment.

Multiple regression model

A general multiple linear regression model at the population level can be written as

\[y_{i}=\beta_{0}+\beta_{1}x_{1i}+\beta_{2}x_{2i}+\ldots+\beta_{k}x_{ki}+\varepsilon_{i} \]

• $y_{i}$: the observed score of individual $i$ on the DV.
• $x_{1},x_{2},\ldots,x_{k}$ : a set of predictors.
• $x_{1i}$: the observed score of individual $i$ on IV 1; $x_{ki}$: observed score of individual $i$ on IV $k$.
• $\beta_{0}$: the intercept at the population level, representing the predicted $y$ score when all the independent variables have their values at 0.
• $\beta_{1},\ldots,\beta_{k}$: regression coefficients at the population level; $\beta_{1}$: representing the amount predicted $y$ changes when $x_{1}$ changes in 1 unit while holding the other IVs constant; $\beta_{k}$: representing the amount predicted $y$ changes when $x_{k}$ changes in 1 unit while holding the other IVs constant.
• $\varepsilon$: unobserved errors with mean 0 and variance $\sigma^{2}$.

Parameter estimation

The least squares method used for the simple linear regression analysis can also be used to estimate the parameters in a multiple regression model. The basic idea is to minimize the sum of squared residuals or errors. Let $b_{0},b_{1},\ldots,b_{k}$ represent the estimated regression coefficients.The individual $i$'s residual $e_{i}$ is the difference between the observed $y_{i}$ and the predicted $y_{i}$

\[ e_{i}=y_{i}-\hat{y}_{i}=y_{i}-b_{0}-b_{1}x_{1i}-\ldots-b_{k}x_{ki}.\]

The sum of squared residuals is

\[ SSE=\sum_{i=1}^{n}e_{i}^{2}=\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}. \]

By minimizing $SSE$, the regression coefficient estimates can be obtained as

\[ \boldsymbol{b}=(\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'\boldsymbol{y}=(\sum\boldsymbol{x}_{i}\boldsymbol{x}_{i}')^{-1}(\sum\boldsymbol{x}_{i}\boldsymbol{y}_{i}). \]

How well the multiple regression model fits the data can be assessed using the $R^{2}$. Its calculation is the same as for the simple regression

\[\begin{align*} R^{2} & = & 1-\frac{\sum e_{i}^{2}}{\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}\\& = & \frac{\text{Variation explained by IVs}}{\text{Total variation}} \end{align*}. \]

In multiple regression, $R^{2}$ is the total proportion of variation in $y$ explained by the multiple predictors.

The $R^{2}$ increases or at least is the same with the inclusion of more predictors. However, with more predators, the model becomes more complex and potentially more difficult to interpret. In order to take into consideration of the model complexity, the adjusted $R^{2}$ has been defined, which is calculated as

\[aR^{2}=1-(1-R^{2})\frac{n-1}{n-k-1}.\]

Hypothesis testing of regression coefficient(s)

With the estimates of regression coefficients and their standard errors estimates, we can conduct hypothesis testing for one, a subset, or all regression coefficients.

Testing a single regression coefficient

At first, we can test the significance of the coefficient for a single predictor. In this situation, the null and alternative hypotheses are

\[ H_{0}:\beta_{j}=0\text{ vs }H_{1}:\beta_{j}\neq0 \]

with $\beta_{j}$ denoting the regression coefficient of $x_{j}$ at the population level.

As in the simple regression, we use a test statistic

\[ t_{j}=\frac{b_{j} - \beta{j} }{s.e.(b_{j})}\]

where $b_{j}$ is the estimated regression coefficient of $x_{j}$ using data from a sample. If the null hypothesis is true and $\beta_j = 0$, the test statistic follows a t-distribution with degrees of freedom \(n-k-1\) where \(k\) is the number of predictors.

One can also test the significance of \(\beta_j\) by constructing a confidence interval for it. Based on a t distribution, the \(100(1-\alpha)%\) confidence interval is

\[ [b_{j}+t_{n-k-1}(\alpha/2)*s.e.(b_{j}),\;b_{j}+t_{n-k-1}(1-\alpha/2)*s.e.(b_{j})]\]

where $t_{n-k-1}(\alpha/2)$ is the $\alpha/2$ percentile of the t distribution. As previously discussed, if the confidence interval includes 0, the regression coefficient is not statistically significant at the significance level $\alpha$.

Testing all the regression coefficients together (overall model fit)

Given the multiple predictors, we can also test whether all of the regression coefficients are 0 at the same time. This is equivalent to test whether all predictors combined can explained a significant portion of the variance of the outcome variable. Since $R^2$ is a measure of the variance explained, this test is naturally related to it.

For this hypothesis testing, the null and alternative hypothesis are

\[H_{0}:\beta_{1}=\beta_{2}=\ldots=\beta_{k}=0\]

\[H_{1}:\text{ at least one of the regression coefficients is different from 0}.\]

In this kind of test, an F test is used. The F-statistic is defined as

\[F=\frac{n-k-1}{k}\frac{R^{2}}{1-R^{2}}.\]

It follows an F-distribution with degrees of freedom $k$ and $n-k-1$ when the null hypothesis is true. Given an F statistic, its corresponding p-value can be calculated from the F distribution as shown below. Note that we only look at one side of the distribution because the extreme values should be on the large value side.

Testing a subset of the regression coefficients

We can also test whether a subset of $p$ regression coefficients, e.g., $p$ from 1 to the total number coefficients $k$, are equal to zero. For convenience, we can rearrange all the $p$ regression coefficients to be the first $p$ coefficients. Therefore, the null hypothesis should be

\[H_{0}:\beta_{1}=\beta_{2}=\ldots=\beta_{p}=0\]

and the alternative hypothesis is that at least one of them is not equal to 0.

As for testing the overall model fit, an F test can be used here. In this situation, the F statistic can be calculated as

\[F=\frac{n-k-1}{p}\frac{R^{2}-R_{0}^{2}}{1-R^{2}},\]

which follows an F-distribution with degrees of freedom $p$ and $n-k-1$. $R^2$ is for the regression model with all the predictors and $R_0^2$ is from the regression model without the first $p$ predictors $x_{1},x_{2},\ldots,x_{p}$ but with the rest predictors $x_{p+1},x_{p+2},\ldots,x_{k}$.

Intuitively, this test determine whether the variance explained by the first \(p\) predictors above and beyond the $k-p$ predictors is significance or not. That is also the increase in R-squared.

As an example, suppose that we wanted to predict student success in college. Why might we want to do this? There's an ongoing debate in college and university admission offices (and in the courts) regarding what factors should be considered important in deciding which applicants to admit. Should admissions officers pay most attention to more easily quantifiable measures such as high school GPA and SAT scores? Or should they give more weight to more subjective measures such as the quality of letters of recommendation? What are the pros and cons of the approaches? Of course, how we define college success is also an open question. For the sake of this example, let's measure college success using college GPA.

In this example, we use a set of simulated data (generated by us). The data are saved in the file gpa.csv. As shown below, the sample size is 100 and there are 4 variables: college GPA (c.gpa), high school GPA (h.gpa), SAT, and quality of recommendation letters (recommd).

Graph the data

Before fitting a regression model, we should check the relationship between college GPA and each predictor through a scatterplot. A scatterplot can tell us the form of relationship, e.g., linear, nonlinear, or no relationship, the direction of relationship, e.g., positive or negative, and the strength of relationship, e.g., strong, moderate, or weak. It can also identify potential outliers.

The scatterplots between college GPA and the three potential predictors are given below. From the plots, we can roughly see all three predictors are positively related to the college GPA. The relationship is close to linear and the relationship seems to be stronger for high school GPA and SAT than for the quality of recommendation letters.

Descriptive statistics

Next, we can calculate some summary statistics to explore our data further. For each variable, we calculate 6 numbers: minimum, 1st quartile, median, mean, 3rd quartile, and maximum. Those numbers can be obtained using the summary() function. To look at the relationship among the variables, we can calculate the correlation matrix using the correlation function cor() .

Based on the correlation matrix, the correlation between college GPA and high school GPA is about 0.545, which is larger than that (0.523) between college GPA and SAT, in turn larger than that (0.35) between college GPA and quality of recommendation letters.

Fit a multiple regression model

As for the simple linear regression, The multiple regression analysis can be carried out using the lm() function in R. From the output, we can write out the regression model as

\[ c.gpa = -0.153+ 0.376 \times h.gpa + 0.00122 \times SAT + 0.023 \times recommd \]

Interpret the results / output

From the output, we see the intercept is -0.153. Its immediate meaning is that when all predictors' values are 0, the predicted college GPA is -0.15. This clearly does not make much sense because one would never get a negative GPA, which results from the unrealistic presumption that the predictors can take the value of 0.

The regression coefficient for the predictor high school GPA (h.gpa) is 0.376. This can be interpreted as keeping SAT and recommd scores constant , the predicted college GPA would increase 0.376 with a unit increase in high school GPA.This is again might be problematic because it might be impossible to increase high school GPA while keeping the other two predictors unchanged. The other two regression coefficients can be interpreted in the same way.

From the output, we can also see that the multiple R-squared ($R^2$) is 0.3997. Therefore, about 40% of the variation in college GPA can be explained by the multiple linear regression with h.GPA, SAT, and recommd as the predictors. The adjusted $R^2$ is slightly smaller because of the consideration of the number of predictors. In fact,

\[ \begin{eqnarray*} aR^{2} & = & 1-(1-R^{2})\frac{n-1}{n-k-1}\\& = & 1-(1-.3997)\frac{100-1}{100-3-1}\\& = & .3809 \end{eqnarray*} \]

Testing Individual Regression Coefficient

For any regression coefficients for the three predictors (also the intercept), a t test can be conducted. For example, for high school GPA, the estimated coefficient is 0.376 with the standard error 0.114. Therefore, the corresponding t statistic is \(t = 0.376/0.114 = 3.294\). Since the statistic follows a t distribution with the degrees of freedom \(df = n - k - 1 = 100 - 3 -1 =96\), we can obtain the p-value as \(p = 2*(1-pt(3.294, 96))= 0.0013\). Since the p-value is less than 0.05, we conclude the coefficient is statistically significant. Note the t value and p-value are directly provided in the output.

Overall model fit (testing all coefficients together)

To test all coefficients together or the overall model fit, we use the F test. Given the $R^2$, the F statistic is

\[ \begin{eqnarray*} F & = & \frac{n-k-1}{k}\frac{R^{2}}{1-R^{2}}\\ & = & \left(\frac{100-3-1}{3}\right)\times \left(\frac{0.3997}{1-.3997}\right )=21.307\end{eqnarray*} \]

which follows the F distribution with degrees of freedom $df1=k=3$ and $df2=n-k-1=96$. The corresponding p-value is 1.160e-10. Note that this information is directly shown in the output as " F-statistic: 21.31 on 3 and 96 DF, p-value: 1.160e-10 ".

Therefore, at least one of the regression coefficients is statistically significantly different from 0. Overall, the three predictors explained a significant portion of the variance in college GPA. The regression model with the 3 predictors is significantly better than the regression model with intercept only (i.e., predict c.gpa by the mean of c.gpa).

Testing a subset of regression coefficients

Suppose we are interested in testing whether the regression coefficients of high school GPA and SAT together are significant or not. Alternative, we want to see above and beyond the quality of recommendation letters, whether the two predictors can explain a significant portion of variance in college GPA. To conduct the test, we need to fit two models:

• A full model: which consists of all the predictors to predict c.gpa by intercept, h.gpa, SAT, and recommd.
• A reduced model: obtained by removing the predictors to be tested in the full model.

From the full model, we can get the $R^2 = 0.3997$ with all three predictors and from the reduced model, we can get the $R_0^2 = 0.1226$ with only quality of recommendation letters. Then the F statistic is constructed as

\[F=\frac{n-k-1}{p}\frac{R^{2}-R_{0}^{2}}{1-R^{2}}=\left(\frac{100-3-1}{2}\right )\times\frac{.3997-.1226}{1-.3997}=22.157.\]

Using the F distribution with the degrees of freedom $p=2$ (the number of coefficients to be tested) and $n-k-1 = 96$, we can get the p-value close to 0 ($p=1.22e-08$).

Note that the test conducted here is based on the comparison of two models. In R, if there are two models, they can be compared conveniently using the R function anova() . As shown below, we obtain the same F statistic and p-value.

To cite the book, use: Zhang, Z. & Wang, L. (2017-2022). Advanced statistics using R . Granger, IN: ISDSA Press. https://doi.org/10.35566/advstats. ISBN: 978-1-946728-01-2. To take the full advantage of the book such as running analysis within your web browser, please subscribe .