The Traffic Assignment Problem: Models and Methods PDF

This monograph provides both a unified account of the development of models and methods for the problem of estimating equilibrium traffic flows in urban areas and a survey of the scope and limitations of present traffic models. The development is described and analyzed by the use of the powerful instruments of nonlinear optimization and mathematical programming within the field of operations research. The first part is devoted to mathematical models for the analysis of transportation network equilibria; the second deals with methods for traffic equilibrium problems. This title will interest readers wishing to extend their knowledge of equilibrium modeling and analysis and of the foundations of efficient optimization methods adapted for the solution of large-scale models. In addition to its value to researchers, the treatment is suitable for advanced graduate courses in transportation, operations research, and quantitative economics....

Chapter List (116 chapters):
- Chapter 1: Cover
- Chapter 2: Title Page
- Chapter 3: Copyright Page
- Chapter 4: Table of Contents
- Chapter 5: Preface
- Chapter 6: Some notations
- Chapter 7: I Models
- Chapter 8: 1 Urban traffic planning
- Chapter 9: 1.1 Introduction
- Chapter 10: 1.2 The transportation planning process
- Chapter 11: 1.3 Organization and goal definition
- Chapter 12: 1.4 Base year inventory
- Chapter 13: 1.5 Model analysis
- Chapter 14: 1.5.1 Trip generation
- Chapter 15: 1.5.2 Trip distribution
- Chapter 16: 1.5.3 Modal split
- Chapter 17: 1.5.4 Traffic assignment
- Chapter 18: 1.6 Travel forecast
- Chapter 19: 1.7 Network evaluation
- Chapter 20: 1.8 Discussion
- Chapter 21: 2 The basic equilibrium model and extensions
- Chapter 22: 2.1 The Wardrop conditions
- Chapter 23: 2.1.1 The fixed demand case
- Chapter 24: 2.1.2 The variable demand case
- Chapter 25: 2.1.3 Discussion
- Chapter 26: 2.2 The mathematical program for user equilibrium
- Chapter 27: 2.2.1 The fixed demand case
- Chapter 28: 2.2.2 Network representations
- Chapter 29: 2.2.3 The elastic demand case
- Chapter 30: 2.2.4 Equivalent fixed demand reformulations
- Chapter 31: 2.2.5 Discussion
- Chapter 32: 2.3 Properties of equilibrium solutions
- Chapter 33: 2.3.1 Existence of equilibrium solutions
- Chapter 34: 2.3.2 Uniqueness of equilibrium solutions
- Chapter 35: 2.3.3 Further properties of equilibrium solutions
- Chapter 36: 2.3.4 Stability and sensitivity of equilibrium solutions
- Chapter 37: 2.4 User equilibrium versus system optimum
- Chapter 38: 2.5 Nonseparable costs and multiclass-user transportation networks
- Chapter 39: 2.6 Related network problem
- Chapter 40: 2.6.1 Traffic equilibria and network games
- Chapter 41: 2.6.2 Discrete traffic equilibrium models
- Chapter 42: 2.6.3 Traffic equilibria and electrical networks
- Chapter 43: 2.6.4 Spatial price equilibria
- Chapter 44: 2.6.5 Optimal message routing in computer communication networks
- Chapter 45: 2.7 Discussion
- Chapter 46: 2.8 Some extension
- Chapter 47: 2.8.1 Stochastic assignment models
- Chapter 48: 2.8.2 Side constrained assignment models
- Chapter 49: 3 General traffic equilibrium models
- Chapter 50: 3.1 Introduction
- Chapter 51: 3.1.1 Alternative definitions of equilibria
- Chapter 52: 3.1.2 Variational inequality problems
- Chapter 53: 3.1.3 Nonlinear complementarity problems
- Chapter 54: 3.1.4 Fixed point problems
- Chapter 55: 3.1.5 Mathematical programming reformulations
- Chapter 56: 3.2 Traffic equilibrium models
- Chapter 57: 3.2.1 Variational inequality models
- Chapter 58: 3.2.2 Nonlinear complementarity models
- Chapter 59: 3.2.3 Fixed point models
- Chapter 60: 3.3 Properties of equilibrium solutions
- Chapter 61: 3.3.1 Existence of equilibrium solutions
- Chapter 62: 3.3.2 Uniqueness of equilibrium solutions
- Chapter 63: 3.3.3 Further properties of equilibrium solutions
- Chapter 64: 3.3.4 Stability and sensitivity of equilibrium solutions
- Chapter 65: II Methods
- Chapter 66: 4 Algorithms for the basic model and its extensions
- Chapter 67: 4.1 The Frank-Wolfe algorithm and its extensions
- Chapter 68: 4.1.1 The Frank-Wolfe algorithm
- Chapter 69: 4.1.2 Termination criteria
- Chapter 70: 4.1.3 The use of the Frank-Wolfe approach for the solution of [TAP] .
- Chapter 71: 4.1.4 Shortest route algorithms
- Chapter 72: 4.1.5 Convergence characteristics of the Frank-Wolfe method
- Chapter 73: 4.1.6 Improvements and extensions
- Chapter 74: 4.2 Algorithm concepts
- Chapter 75: 4.2.1 Partial linearization algorithms
- Chapter 76: 4.2.2 Decomposition algorithms
- Chapter 77: 4.2.3 Column generation algorithms
- Chapter 78: 4.2.4 Discussion
- Chapter 79: 4.2.5 A taxonomy of algorithms for [TAP]
- Chapter 80: 4.3 Algorithms for the basic model
- Chapter 81: 4.3.1 Decomposition algorithms
- Chapter 82: 4.3.2 Sequential decomposition algorithms
- Chapter 83: 4.3.3 Parallel decomposition algorithms
- Chapter 84: 4.3.4 Aggregate simplicial decomposition algorithms
- Chapter 85: 4.3.5 Disaggregate simplicial decomposition algorithms
- Chapter 86: 4.3.6 Comparisons between aggregated and disaggregated representations
- Chapter 87: 4.3.7 Dual algorithms
- Chapter 88: 4.3.8 Network aggregation algorithms
- Chapter 89: 4.3.9 Other algorithms
- Chapter 90: 4.4 Algorithms for elastic demand problems
- Chapter 91: 4.5 Algorithms for stochastic assignment models
- Chapter 92: 4.5.1 Stochastic network loading
- Chapter 93: 4.5.2 Stochastic user equilibrium
- Chapter 94: 4.6 Algorithms for side constrained assignment models
- Chapter 95: 4.6.1 Algorithms for capacity side constrained assignment models
- Chapter 96: 4.7 Discussion
- Chapter 97: 5 Algorithms for general traffic equilibria
- Chapter 98: 5.1 Introduction
- Chapter 99: 5.2 Algorithm concepts
- Chapter 100: 5.2.1 Cost approximation algorithms
- Chapter 101: 5.2.2 Decomposition algorithms
- Chapter 102: 5.2.3 Column generation algorithms
- Chapter 103: 5.2.4 Algorithmic equivalence results
- Chapter 104: 5.2.5 Descent algorithms for variational inequalities
- Chapter 105: 5.3 Algorithms for general traffic equilibria
- Chapter 106: 5.3.1 Linear approximation algorithms
- Chapter 107: 5.3.2 Sequential decomposition algorithms
- Chapter 108: 5.3.3 Parallel decomposition algorithms
- Chapter 109: 5.3.4 Algorithms based on the primal and dual gap functions
- Chapter 110: 5.3.5 Column generation algorithms
- Chapter 111: 5.3.6 Dual algorithms
- Chapter 112: 5.3.7 Other algorithms
- Chapter 113: 5.4 Discussion
- Chapter 114: A Definitions
- Chapter 115: References
- Chapter 116: Index
Rate & write a review
Similar documents.

The Traffic Assignment Problem: Models and Methods

Contextualization: Meanings, Methods and Models

Social Dynamics Models and Methods

Economic Dynamics: Methods and Models

Introduction to Network Traffic Flow Theory: Principles, Concepts, Models, and Methods

System Reliability Theory: Models and Statistical Methods

Physical Inorganic Chemistry: Principles, Methods, and Models

Financial Econometrics: Problems, Models, and Methods

Traffic Flow Theory: Characteristics, Experimental Methods, and Numerical Techniques

Rose\'s Assignment

Assignment in the Alps

Software Reuse: Methods, Models, Costs, second edition

Assignment in Brittany

Software Reuse: Methods, Models, Costs, Second Edition

Remote Sensing: Models and Methods for Image Processing

Social Learning: An Introduction to Mechanisms, Methods, and Models
Popular uploaders.
- William W Veale
- Margarite Camaj
- Lyle D. Vander Broek
- Makayla Brooke
- Dorothy J. Wang
- Michele Grossman
- Angel Landaeta Gómez
- Allison Patchett
- Frederic A. Lucas
- Karsten Joost
- Gregory Vlastos
- Osoba O. Otaigbe
- Ernst Von Glasersfeld
- Marina Julia
- Gaby Epstein
- Sir Monier Monier-Williams
- Felix A. (Tito) Conde-Torres
- Camilla Lundberg
- Sarah Pritchard
- Stacey Cargnelutti
- Travis Fortner
- Alister McGrath and Ravi Zacharias
- William Bowden
- Nigel Loreihe
- Gregory Blaxland
- James C. Spall
- Choon Weng Lee
- Wilfried Blecher
- Willi Draths

Traffic Assignment: A Survey of Mathematical Models and Techniques
- First Online: 17 May 2018
Cite this chapter

- Pushkin Kachroo 14 &
- Kaan M. A. Özbay 15
Part of the book series: Advances in Industrial Control ((AIC))
1110 Accesses
2 Citations
This chapter presents the fundamentals of the theory and techniques of traffic assignment problem. It first presents the steady-state traffic assignment problem formulation which is also called static assignment, followed by Dynamic Traffic Assignment (DTA), where the traffic demand on the network is time varying. The static assignment problem is shown in a mathematical programming setting for two different objectives to be satisfied. The first one where all users experience same travel times in alternate used routes is called user-equilibrium and another setting called system optimum in which the assignment attempts to minimize the total travel time. The alternate formulation uses variational inequality method which is also presented. Dynamic travel routing problem is also reviewed in the variational inequality setting. DTA problem is shown in discrete and continuous time in terms of lumped parameters as well as in a macroscopic setting, where partial differential equations are used for the link traffic dynamics. A Hamilton–Jacobi- based travel time dynamics model is also presented for the links and routes, which is integrated with the macroscopic traffic dynamics. Simulation-based DTA method is also very briefly reviewed. This chapter is taken from the following Springer publication and is reproduced here, with permission and with minor changes: Pushkin Kachroo, and Neveen Shlayan, “Dynamic traffic assignment: A survey of mathematical models and technique,” Advances in Dynamic Network Modeling in Complex Transportation Systems (Editor: Satish V. Ukkusuri and Kaan Özbay) Springer New York, 2013. 1-25.
This chapter is taken from the following Springer publication and is reproduced here, with permission and with minor changes: Pushkin Kachroo, and Neveen Shlayan, “Dynamic traffic assignment: A survey of mathematical models and techniques,” Advances in Dynamic Network Modeling in Complex Transportation Systems (Editor: Satish V. Ukkusuri and Kaan Özbay) Springer New York, 2013. 1–25.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Institutional subscriptions
Similar content being viewed by others

Dynamic Traffic Assignment: A Survey of Mathematical Models and Techniques

Traffic Assignments to Transportation Networks
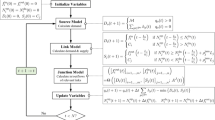
Computing Dynamic User Equilibria on Large-Scale Networks with Software Implementation
Gazis DC (1974) Traffic science. Wiley-Interscience Inc, New York, NY
MATH Google Scholar
Potts RB, Oliver RM (1972) Flows in transportation networks. Elsevier Science
Google Scholar
Stouffer SA (1940) Intervening opportunities: a theory relating mobility and distance. Am Sociol Rev 5:845–867
Article Google Scholar
Hitchcock FL (1941) The distribution of a product from several sources to numerous localities. J Math Phys 20:224–230
Article MathSciNet Google Scholar
Voorhees AM (2013) A general theory of traffic movement 40:1105–1116. https://doi.org/10.1007/s11116-013-9487-0
Wilson AG (1967) A statistical theory of spatial distribution models. Transp Res 1:253–269
Ben-Akiva ME, Lerman SR (1985) Discrete choice analysis: theory and application to travel demand. MIT Press series in transportation studies, MIT Press
Wardrop JG (1952) Some theoretical aspects of road traffic research. Proc Inst Civil Eng PART II 1:325–378
Sheffi Y (1985) Urban transportation networks: equilibrium analysis with mathematical programming methods. Prentice-Hall
Peeta S, Ziliaskopoulos AK (2001) Foundations of dynamic traffic assignment: the past, the present and the future. Netw Spat Econ 1(3/4):233–265
Kachroo P, Sastry S (2016a) Travel time dynamics for intelligent transportation systems: theory and applications. IEEE Trans Intell Transp Syst 17(2):385–394
Kachroo P, Sastry S (2016b) Traffic assignment using a density-based travel-time function for intelligent transportation systems. IEEE Trans Intell Transp Syst 17(5):1438–1447
Dafermos SC, Sparrow FT (1969) The traffic assignment problem for a general network. J Res Natl Bur Stan 73B:91–118
Beckmann MJ, McGuire CB, Winsten CB (1955) Studies in the economics of transportation. Technical report, Rand Corporation
Dafermos S (1980) Traffic equilibrium and variational inequalities. Transp Sci 14:42–54
Dafermos S (1983) An iterative scheme for variational inequalities. Math Prog 26:40–47
Kinderlehrer D, Stampacchia G (2000) An introduction to variational inequalities and their applications, vol 31. Society for Industrial Mathematics
Avriel M (2003) Nonlinear programming: analysis and methods. Dover Publications
Bazaraa MS, Sherali HD, Shetty CM (2006) Nonlinear programming: theory and algorithms. John Wiley & Sons
Mangasarian OL (1994) Nonlinear programming, vol 10. Society for Industrial Mathematics. https://doi.org/10.1137/1.9781611971255
Nugurney A (2000) Sustainable transportation networks. Edward Elgar Publishing, Northampton, MA
Facchinei F, Pang JS (2007) Finite-dimensional variational inequalities and complementarity problems. Springer Science & Business Media
Nagurney A, Zhang D (2012) Projected dynamical systems and variational inequalities with applications, vol 2. Springer Science & Business Media
Zhang D, Nagurney A (1995) On the stability of projected dynamical systems. J Optim Theory Appl 85(1):97–124
Nagurney A, Zhang D (1997) Projected dynamical systems in the formulation, stability analysis, and computation of fixed-demand traffic network equilibria. Transp Sci 31(2):147–158
Zhang D, Nagurney A (1996) On the local and global stability of a travel route choice adjustment process. Transp Res Part B: Methodol 30(4):245–262
Dafermos S (1988) Sensitivity analysis in variational inequalities. Math Oper Res 13:421–434
Dupuis P, Nagurney A (1993) Dynamical systems and variational inequalities. Ann Oper Res 44(1):7–42
Skorokhod AV (1961) Stochastic equations for diffusion processes in a bounded region. Theory Probab Appl 6:264–274
Chiu Y-C, Bottom J, Mahut M, Paz A, Balakrishna R, Waller T, Hicks J (2010) A primer for dynamic traffic assignment. Trans Res Board, 2–3
Ran B, Boyce DE (1996) Modeling dynamic transportation networks: an intelligent transportation system oriented approach. Springer
Chapter Google Scholar
Friesz TL (2001) Special issue on dynamic traffic assignment. Netw Spat Econ Part I 1:231
Merchant DK, Nemhauser GL (1978a) A model and an algorithm for the dynamic traffic assignment problems. Transp Sci 12(3):183–199
Merchant DK, Nemhauser GL (1978b) Optimality conditions for a dynamic traffic assignment model. Transp Sci 12(3):183–199
Boyce D, Lee D, Ran B (2001) Analytical models of the dynamic traffic assignment problem. Netw Spat Econ 1:377–390
Friesz TL, Luque J, Tobin RL, Wie BW (1989) Dynamic network traffic assignment considered as a continuous time optimal control problem. Oper Res 37:893–901
Friesz TL, Bernstein D, Smith TE, Tobin RL, Wie BW (1993) A variational inequality formulation of the dynamic network user equilibrium problem. Oper Res 41:179–191
Chen HK (2012) Dynamic travel choice models: a variational inequality approach. Springer Science & Business Media
Carey M (1992) Nonconvexity of the dynamic traffic assignment problem. Transp Res Part B: Methodol 26(2):127–133
Lighthill MJ, Whitham GB (1955) On kinematic waves II. A theory of traffic on long crowded roods. Proc Roy Soc London A Math Phys Sci 229:317–345. https://doi.org/10.1098/rspa.1955.0089
Richards PI (1956) Shockwaves on the highway. Oper Res 4:42–51
Greenshields B, Channing W, Miller H (1935) A study of traffic capacity. In: Highway Research Board Proceedings. National Research Council (USA), Highway Research Board
LeVeque RJ (1990) Numerical methods for conservation laws. Birkhäuser Verlag
Bressan A (2000) Hyperbolic systems of conservation laws: the one-dimensional Cauchy problem. Oxford University Press
Strub I, Bayen A (2006) Weak formulation of boundary conditions for scalar conservation laws: an application to highway modeling. Int J Robust Nonlinear Control 16:733–748
Garavello M, Piccoli B (2006) Traffic flow on networks. American Institute of Mathematical Sciences, Ser Appl Maths 1:1–243
Holden H, Risebro NH (1995) A mathematical model of traffic flow on a network of unidirectional roads. SIAM J Math Anal 26:999–1017
Lebacque JP (1996) The godunov scheme and what it means for first order traffic flow models. In: Transportation and Traffic Theory, Proceedings of The 13th International Symposium on Transportation and Traffic Theory, Lyon, France, pp 647–677
Coclite GM, Piccoli B (2002) Traffic flow on a road network. Arxiv preprint math/0202146
Garavello M, Piccoli B (2005) Source-destination flow on a road network. Commun Math Sci 3(3):261–283
Gugat M, Herty M, Klar A, Leugering G (2005) Optimal control for traffic flow networks. J Optim theory Appl 126(3):589–616
Lebacque JP, Khoshyaran MM (2002) First order macroscopic traffic flow models for networks in the context of dynamic assignment. In: Patriksson M, Labbé M (eds) Transportation, Planning: State of the Art. Springer US, Boston, MA, pp 119–140. https://doi.org/10.1007/0-306-48220-7_8
Buisson C, Lebacque JP, Lesort JB (1996) Strada, a discretized macroscopic model of vehicular traffic flow in complex networks based on the godunov scheme. In: CESA’96 IMACS Multiconference: computational engineering in systems applications, pp 976–981
Mahmassani HS, Hawas YE, Abdelghany K, Abdelfatah A, Chiu YC, Kang Y, Chang GL, Peeta S, Taylor R, Ziliaskopoulos A (1998) DYNASMART-X; Volume II: analytical and algorithmic aspects. Technical report ST067 85
Ben-Akiva M, Bierlaire M, Koutsopoulos H, Mishalani R (1998) DynaMIT: a simulation-based system for traffic prediction. In: DACCORS short term forecasting workshop, vol TRANSP-OR-CONF-2006-060
Kachroo P, Özbay K (2012) Feedback control theory for dynamic traffic assignment. Springer Science & Business Media
Kachroo P, Özbay K (2011) Feedback ramp metering in intelligent transportation systems. Springer Science & Business Media
Kachroo P, Özbay K (1998) Solution to the user equilibrium dynamic traffic routing problem using feedback linearization. Transp Res Part B: Methodol 32(5):343–360
Kachroo P, Özbay K (2006) Modeling of network level system-optimal real-time dynamic traffic routing problem using nonlinear \(\text{ h }{\infty }\) feedback control theoretic approach. J Intell Transp Syst 10(4):159–171
Kachroo P, Özbay K (2005) Feedback control solutions to network level user-equilibrium real-time dynamic traffic assignment problems. Netw Spat Econ 5(3):243–260
Spiess H (1990) Conical volume-delay functions. Transp Sci 24(2):153–158
Download references
Author information
Authors and affiliations.
Department of Electrical and Computer Engineering, University of Nevada, Las Vegas, NV, USA
Pushkin Kachroo
Department of Civil and Urban Engineering, New York University, Brooklyn, NY, USA
Kaan M. A. Özbay
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Pushkin Kachroo .
Rights and permissions
Reprints and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Kachroo, P., Özbay, K.M.A. (2018). Traffic Assignment: A Survey of Mathematical Models and Techniques. In: Feedback Control Theory for Dynamic Traffic Assignment. Advances in Industrial Control. Springer, Cham. https://doi.org/10.1007/978-3-319-69231-9_2
Download citation
DOI : https://doi.org/10.1007/978-3-319-69231-9_2
Published : 17 May 2018
Publisher Name : Springer, Cham
Print ISBN : 978-3-319-69229-6
Online ISBN : 978-3-319-69231-9
eBook Packages : Engineering Engineering (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
(Stanford users can avoid this Captcha by logging in.)
- Send to text email RefWorks EndNote printer
The traffic assignment problem : models and methods
Available online, at the library.

SAL3 (off-campus storage)
More options.
- Find it at other libraries via WorldCat
- Contributors
Description
Creators/contributors, contents/summary.
- Part 1 Models: urban traffic planning - the transportation planning process, organization and goal definition, base-year inventory, model analysis, travel forecast, network evaluation, discussion
- the basic equilibrium model and extensions - the Wardrop conditions, the mathematical program for user equilibrium, properties of equilibrium solutions, user equilibrium versus system optimum, non-separable costs and multiclass-user transportation networks, related network problems, discussion, some extentions
- general traffic equilibrium models - traffic equilibrium models, properties of equilibrium solutions. Part 2 Methods: algorithms for the basic model and its extensions - the Frank-Wolfe algorithm and its extensions, algorithm concepts, algorithms for the basic model, algorithms for elastic demand problems, algorithms for stochastic assignment models, algorithms for side-constrained assignment models, discussion
- algorithms for general traffic equilibria - algorithm concepts, algorithms for general traffic equilibria, discussion.
- (source: Nielsen Book Data)
Bibliographic information
- Stanford Home
- Maps & Directions
- Search Stanford
- Emergency Info
- Terms of Use
- Non-Discrimination
- Accessibility
© Stanford University , Stanford , California 94305 .

IMAGES
VIDEO
COMMENTS
This paper proposes a coordinated pricing-and-routing scheme for truck drivers to efficiently route trucks into the network and improve the overall traffic conditions and provides personalized routing instructions based on drivers' individual routing preferences.
Request PDF | The Traffic Assignment Problem: Models and Methods | This monograph provides both a unified account of the development of models and methods for the problem of estimating equilibrium ...
Traffic Assignment Traffic assignment How: By distributing the total O-D demand between various routes for that O-D pair Network loading mechanism: The process of loading O- D trip table to the network links Difficulty: Individuals are not homogenous Behavior: Different individuals behave differently based on their socio-economic characteristics and past experience
This monograph provides both a unified account of the development of models and methods for the problem of estimating equilibrium traffic flows in urban areas and a survey of the scope and limitations of present traffic models. The development is described and analyzed by the use of the powerful instruments of nonlinear optimization and mathematical programming within the field of operations ...
The basic equilibrium model and extensions - the Wardrop conditions, the mathematical program for user equilibrium, properties of equilibrium solutions, user equilibrium versus system optimum, non-separable costs and multiclass-user transportation networks, related network problems, discussion. Part 1 Models: urban traffic planning - the transportation planning process, organization and goal ...
28 2 Traffic Assignment: A Survey of Mathematical Models and Techniques 2.2.1.1 Mathematical Programming Formulation The optimization problem statement for user-equilibrium aimed at achieving Wardrop's principle is shown in Eq.(2.1). minimize z(x) = a x a 0 t aω) dω (2.1) with equality constraints given by: k frs k = q rs ∀r,s (2.2) x a ...
The second part deals with methods for traffic equilibrium problems. This title should be of interest to researchers in transportation, operations reserch and quantitative economics, who wish to extend their knowledge of equilibrium modelling and analysis, and of the foundations of efficient optimization methods adapted for the solution of ...
The class of traffic assignment problem tries to model these behaviour. Therefore, the traffic assignment will be discussed before adressing bi-level formulation of the network design problems. 2 Traffic assignment The process of allocating given set of trip interchanges to the specified transportation system is usually refered to as traffic ...
The second part deals with methods for traffic equilibrium problems. This title should be of interest to researchers in transportation, operations reserch and quantitative economics, who wish to extend their knowledge of equilibrium modelling and analysis, and of the foundations of efficient optimization methods adapted for the solution of ...
Read The Traffic Assignment Problem by Michael Patriksson with a free trial. Read millions of eBooks and audiobooks on the web, iPad, iPhone and Android. This monograph provides both a unified account of the development of models and methods for the problem of estimating equilibrium traffic flows in urban areas and a survey of the scope and ...