lesson 8 homework 3.3

Texas Go Math
Big Ideas Math
enVision Math
EngageNY Math
McGraw Hill My Math
180 Days of Math
Math in Focus Answer Key
Math Expressions Answer Key
Privacy Policy

$Go Math Answer Key$

Texas Go Math Grade 8 Lesson 3.3 Answer Key Interpreting the Unit Rate as Slope

Refer to our Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 3.3 Answer Key Interpreting the Unit Rate as Slope.

How do you interpret the unit rate as slope?

Texas Go Math Grade 8 Lesson 3.3 Explore Activity Answer Key

Relating the Unit Rate to Slope A rate is a comparison of two quantities that have different units, such as miles and hours. A unit rate is a rate in which the second quantity in the comparison is one unit.

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 1$

A. Find the slope of the graph using the points (1, 2) and (5, 10). Remember that the slope is the constant rate of change.

B. Find the unit rate of snowfall in inches per hour. Explain your method.

C. Compare the slope of the graph and the unit rate of change in the snow level. What do you notice?

D. Which point on the graph tells you the slope of the graph and the unit rate of change in the snow level? Explain how you found the point.

Question 1. What If? Without referring to the graph, how do you know that the point (1, $\frac{4}{3}$) is on the graph? Answer: Lets find the slope: Slope = $\frac{8-4}{6-3}$ = $\frac{4}{3}$ This holds for every two points on the graph, so it has to hold for some of the given points and the point we want to check. Substitute the point (6, 8) for (1, $\frac{4}{3}$) and see if it still holds. $\frac{\frac{4}{3}-4}{1-3}$ = $\frac{4}{3}$ = Slope for x = Time and y = Amount Therefore, the point (1, $\frac{4}{3}$) is on the line. By checking if the equation for the slope (which we calculated) holds for the given point we see that it does, so it is on the line.

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 2$

Question 3. Describe the relationships among the slope of the graph of Well A’s rate, the equation representing Well A’s rate, and the constant of proportionality. Answer: The slope of the graph of Well, A’s rate, the equation representing Well A’s rate, and the constant of proportionality are the same. They all represent the amount of oil pumped from Well A in an hour.

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 3$

Texas Go Math Grade 8 Lesson 3.3 Guided Practice Answer Key

Give the slope of the graph and the unit rate. (Explore Activity and Example 1)

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 4$

Write an equation relating the variables in each table. (Example 2)

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 7$

Essential Question Check-In

Question 6. Describe methods you can use to show a proportional relationship between two variables, x and y. For each method, explain how you can find the unit rate and the slope. Answer: Explanation A: We can represent a proportional relationship between two variables x and y using a table. For each point we find the ratio of y over x. If this ratio is constant over each point, then the relationship is proportional. To find the unit rate and slope, we have: Slope = Unit Rate = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

We can represent a proportional relationship between two variables x and y using an equation of the form y = kx, where k is a number called the constant of proportionality. The slope and unit rate are equal to the constant of proportionality, however we can construct a table from the given equation and proceed as described above.

We can represent a proportional relationship between two variables x and y using a graph. The graph will be a line that passes through the origin (0, 0). To find the unit rate and slope, we have: Slope = Unit Rate = $\frac{\text { rise }}{\text { run }}$

Explanation B: You can use a table to find the ratio of each point. If the ratio is constant, the relationship is proportional. You can find the unit rate and slope by: Slope(m) = UnitRate = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

You can use a graph to find the ratio of the rise for equal intervals of run. You can find the unit rate and slope by: Slope(m) = UnitRate = $\frac{\text { rise }}{\text { run }}$

Texas Go Math Grade 8 Lesson 3.3 Independent Practice Answer Key

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 9$

c. Find the slope of the graph and describe what it means in the context of this problem. Answer: The slope of the graph is $\frac{6-3}{8-4}$ = $\frac{3}{4}$ in this case, this means that a Canadian goose migrates 3 miles every 4 minutes or $\frac{3}{4}$ miles every minute. The goose migrates $\frac{3}{4}$ miles every minute.

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 11$

a. Determine the slope and unit rate of each machine Answer: (1) Using the given table, calculate the slope and unit rate of the first machine. Slope = Unit rate = $\frac{1.2-0.6}{2-1}$ = $\frac{0.6}{1}$ = 0.6 The unit rate for the first machine is therefore 0.6 gallons per second.

(2) Using the given graph, find points to substitute into the formula for the slope. Two points on the line for the second machine are: (8, 6) and (16, 12). Now calculate the slope and unit rate of the second machine using the points you just found. Slope = Unit rate = $\frac{12-6}{16-8}$ = $\frac{6}{8}$ = 0.75 The unit rate for the second machine is therefore 0.75 gallons per second The slope and unit rate of the first machine is 0.6 (gallons per second), and of the second 0.75 (gallons per second).

b. Determine which machine is working at a faster rate. Answer: Comparing the unit rates of both machines we can see that the second machine bottles more milk per second than the first machine. Therefore it is working at a faster rate. The second machine is faster.

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 13$

Lets find the slope and the unit rate of jennifer Slope = $\frac{8-5}{64-40}$ = $\frac{3}{24}$ = $\frac{1}{8}$ Therefore, Jennifer’s unit rate is $\frac{1}{8}$ kilometers per minute. We can conclude that Patrick has a faster training rate.

Question 11. Analyze Relationships There is a proportional relationship between minutes and cost in dollars. The graph passes through the point (1, 4.75). What is the slope of the graph? What is the unit rate? Explain. Answer: If we know that there is a proportional relationship between minutes and dollars per minute, then the graph is a straight line. Also since that line passes through (1, 4.75) we know that for 1 minute it costs 4.75 dollars to print. Therefore the slope is 4.75 and the unit rate is 4.75 dollars per minute.

The slope is 4.75 and the unit rate is 4.75 dollars per minute.

Question 12. Draw Conclusions Two cars start at the same time and travel at different constant rates. The graph of the distance in miles given the time in hours for Car A passes through the point (0.5, 27.5), and the graph for Car B passes through the point (4, 240). Which car is traveling faster? Explain. Answer: Unit Rate = $\frac{27.5}{0.5}$ = 55 Find the unit rate for Car A. Car $A$ travels $55$ miles in $1$ hr

Unit Rate = $\frac{240}{4}$ = 60 Find the unit rate for Car B. Car $B$ travels $60$ miles in $1$ hr Car B is faster Compare the unit rates 60 > 55

$Texas Go Math Grade 8 Lesson 3.3 Answer Key 14$

Additional water = 18 * 1$\frac{1}{2}$ = 27 After 1$\frac{1}{2}$ min after 12 min

Total = 216 + 27 = 243gal The total water after 13$\frac{1}{2}$ min

Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations

We included H MH Into Math Grade 8 Answer Key PDF Module 3 Lesson 3 Apply Linear Equations to make students experts in learning maths.

HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations

I Can solve linear equations and interpret solutions in context.

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 1$

Turn and Talk Which variable or expression represents the number of dimes? Which variable or expression represents the number of nickels? Explain your reasoning.

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 15$

Turn and Talk How would the solution be different if Rachel did not have a coupon?

Check Understanding

Question 1. The equation x + (75.3 – x) = 75.3 represents the sum of two angle measures. How many possible combinations of angle measures satisfy these conditions? Answer: The above-given equation: x + (75.3 – x) = 75.3 simplify both sides of the equation: x + 75.3 − x = 75.3 75.3 = 75.3 subtract 75.3 from both sides 0 = 0 All real numbers are solutions.

Question 2. Two bicyclists on a 75-mile trail ride toward each other. One bicyclist begins at the 45-mile marker. The other begins at the end of the trail. The expressions shown represent the distance from the Parking Lot for each bicyclist when they meet. A. Write an equation to represent the bicyclists’ meeting after x hours. __________________ Answer: 75 – 10x = 45 + 10x combine like terms -10x – 10x = 45 – 75 -20x = -30 x = 30/20 x = 3/2 = 1.5 hours

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 5$

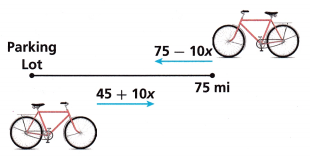
B. After how many hours do the bicyclists meet? __________________ Answer: The bicyclist meet after 1 hour 5 minutes

C. How far away are the bicyclists from the parking lot when they meet? __________________ Answer:

On Your Own

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 6$

B. What does the solution represent about James and Brianne’s locations? ____________________________________ ____________________________________ Answer:

C. What is their height above the ground floor when they are at the same height at the same time? ____________________________________ Answer:

Question 4. The expression 100 – 2.5x represents the balance of Grace’s account after x days. The expression 100 + 2.5(5 – x) represents the balance of Tim’s account after x days. After how many days do the accounts have the same balance? Answer:

Question 5. Josh is 3 years older than Lynette. The sum of their ages is 49. Write expressions for Josh’s age and Lynette’s age, and use the expressions to write an equation relating their ages. Use the equation to determine Josh’s age and Lynette’s age. Answer: Josh = 3 + l L = l sum of thier ages = 49 The equation would be: 3 + l + l = 49 3 + 2l = 49 2l = 49 – 3 2l = 46 l = 46/2 l = 23 Hence, the age of Lynette is 23 Now find out josh age Josh = 3 + l josh = 3 + 23 josh = 26 Therefore, the age of Josh is 26.

Question 6. Zander downloads a combination of 30 games and songs. He downloads 8 more songs than games. The equation g + (8 + g) = 30 can be solved to determine g, the number of games Zander downloaded. How many games did Zander download? How many songs did he download? Answer: The above-given equation: g + (8 + g) = 30 combine like terms 2g+ 8 = 30 get all like terms on one side 2g = 30 – 8 2g = 22 g = 11 Therefore, 11 songs were downloaded.

Question 7. Open Ended A business breaks even when its production costs are equal to its revenue. The expression 120 + 4x represents the cost of producing x items. Decide on a selling price for each item, and write an expression for the revenue generated by selling x items. How many items would you need to sell at your chosen price to break even? Write an equation and solve it. Answer:

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 9$

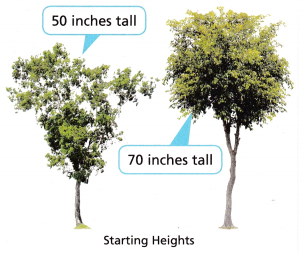
B. After how many years will the heights of the two trees be equal? __________________ Answer:

C. What will be the height of the trees when they are the same height? Answer:

Question 9. Rodney opens a savings account with $75 and also deposits $40 each month. Morgan opens an account with $50 and also deposits $40 each month. Will they have the same amount in their account at any point? If so, after how many months? Explain. Answer: The equation would be: 75(m + 40) = 50(m + 40) 75m + 3000 = 50m + 2000 75m – 50m = 2000 – 3000 25m = -1000 m = -1000/25 m = -40 There is no chance of having the same amount at any point.

Question 10. Critique Reasoning Ethan said 5x – 20 = 5(x – 20) has infinitely many solutions. Is he correct? Explain. Answer: The above-given equation: 5x – 20 = 5(x – 20) apply distributive property 5x – 20 = 5x – 100 combine like terms 5x – 5x = -100 + 20 0 = -80 Therefore, it has no solutions Hence, Ethan statement is proved as wrong.

Question 11. Abigail wants to find three consecutive even integers whose sum is four times the smallest of those integers. She lets n represent the smallest integer, then writes this equation: n + (n + 2) + (n + 4) = 4n. A. Solve the equation. __________________ Answer: The given equation: n + (n + 2) + (n + 4) = 4n. 3n + 6 = 4n combine like terms 6 = 4n – 3n 6 = n switch the sides n = 6

B. What are the three integers? __________________ Answer: x, x+1, and x+2 are the three consecutive integers.

Question 12. Every year Aiden uses income from his job to pay for 75% of his college tuition. Next year’s tuition will be $720 more than this year’s, and Alden will pay $2400. How much is this year’s tuition? __________________ Answer: Aiden uses his income to pay 75% of college tuition

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 10$

Question 14. Isaac wants to play miniature golf. Go Golf charges $2.50 for ball and club rental and $4.25 per game. Golf Games charges $3.25 for ball and club rental and $8.50 for two games. For how many games would the cost be the same? Write and solve an equation to determine the number of games for which the cost would be the same. Answer:

Question 15. The members of a knitting club are buying supplies for their next meeting. For the club, they need to buy a new patterns book for $3.50. For each member, they need to buy a set of knitting needles for $3.20 and a ball of yarn for $5.40. They spent $63.70 in total. Write and solve an equation to determine how many members the knitting club has. Answer:

Question 16. Liam is a rewards member at a local restaurant. He can buy four tacos at the regular price and get $5.50 off his purchase. Zachary found a coupon to buy three tacos at the regular price and get $6.50 off his total. What would the taco price need to be in order for Liam and Zachary to spend the same amount? A. Write the equation. _____________ Answer:

B. Solve the equation. _____________ Answer:

C. What does the solution to the equation represent? _____________ Answer:

Lesson 3.3 More Practice/Homework

Apply Linear Equations

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 11$

B. How many pennies does Janesa have in her pocket? _____________ Answer:

C. What is the total value of the pennies? _____ Answer:

D. What is the total value of the nickels? _____ Answer:

E. What should Jackson guess to get his sister’s coins? __________________ Answer:

Question 3. Math on the Spot Flex Gym charges a membership fee of $150.00 plus $40.50 per month to join the gym. A rival gym, Able Gym, charges a membership fee of $120.00 plus $46.75 per month. Find the number of months for which you would pay the same total fee to both gyms. Answer:

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 13$

Question 5. A biologist recorded the population growth of two species of frogs in a pond area starting in 2010. The first species started with 42 frogs and increased by 6 frogs per year. The second species started with 30 frogs and increased by 8 frogs per year. A. Write an equation modeling equal populations of the frogs t years after 2010. ____________________________________ Answer:

B. In what year were the populations of the two groups of frogs equal? ____________________________________ Answer:

Use the information to answer Problems 6-7.

Riley is comparing cell phone plans. The table shows four options Riley is considering. The gigabytes of data used each month is represented by g.

$HMH Into Math Grade 8 Module 3 Lesson 3 Answer Key Apply Linear Equations 14$

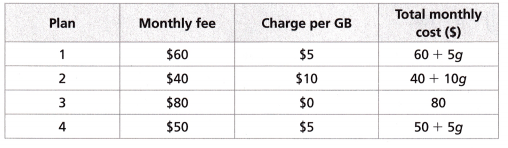
Question 6. Which two plans will never cost the same amount for any amount of data? A. Plans 1 and 3 B. Plans 2 and 4 C. Plans 3 and 2 D. Plans 4 and 1 Answer:

Question 7. Which plan should Riley get if he only uses 3 gigabytes of data each month? A. Plan 1 B. Plan 2 C. Plan 3 D. Plan 4 Answer: Option D is correct. Explanation: Riley uses only 3GB and he will not use extra GB. So he would choose less amount with minimum GB.

Spiral Review

Question 8. The segment with endpoints (0, 8) and (-6, 0) is dilated to a segment with endpoints (0, 6) and (-4.5, 0). What is the scale factor of the dilation? Answer:

Question 9. For what value of m does the equation 5 – 3x = m + mx have no solutions? Answer: The given equation: 5 – 3x = m + mx Flip the equation: m + mx = 5 – 3x factor out variable m m(x + 1) = -3x + 5 divide both sides by x+1 m(x +1)/x + 1 = -3x + 1/x + 5 m = -3x + 1/x + 5