multiples of 2 problem solving

Multiples Questions

Multiples questions are provided here with their solutions to help students practice and understand the concept of factors and multiples . Practising these questions will be beneficial for students in lower grades. We recommend students to practice these questions within a time limit this will increase their solving speed.

Also, Check Factors and Multiples Worksheets .

Multiples of any number are the product of the given number with natural numbers. For example, the multiples of 3 are 3, 6, 9, 12, 15, … In other words, we can say multiples of a number are those numbers which come in times table of that number.

Multiples Questions with Solution

Let us solve some questions based on multiples of a number.

Question 1: List the first 10 multiples of the following numbers:

(i) The first 10 multiples of 12 are

(ii) The first 10 multiples of 52 are

(iii) The first 10 multiples of 9 are

Question 2: Find the first three common multiples of 2 and 14.

Multiples of 2: 2, 4, 6, 8, 10, 12, 14 , 16, 18, 20, 22, 24, 26, 28 , 30, 32, 34, 36, 38, 40, 42 , …

Multiples of 14: 14 , 28 , 42 , 56, 70, 84, 98, …

Therefore, the first three common multiples of 2 and 14 are 14, 28 and 42.

• HCF of Numbers
• Prime Factorization and Division Method for LCM and HCF
• Prime Factorization

Question 3: Find the smallest number whose factors are 2, 3 and 7.

The smallest number whose factors are 2,3 and 7 is the LCM(2, 3, 7)

Now, LCM (2, 3, 7) = 2 × 3 × 7 = 42

∴ 42 is the smallest number whose factors are 2, 3 and 7.

Question 4: There are 62 students in a classroom. If 310 notebooks are to be distributed among them, find how many notebooks each student gets.

Total number of students = 62

Total number of notebooks = 310

We observe that 310 is the 5th multiple of 62, that is, 62 × 5 = 310.

∴ each student gets 5 notebooks.

Question 5: How many complete weeks are there in a leap year?

Number of days in a week = 7

Number of days in a leap year = 366

Now, 7 × 52 = 364 and 7 × 53 = 371 such that 364 < 366 < 371

Therefore, there are 52 complete weeks are there in a leap year.

Question 6: Is 111 divisible by 3?

Now 3 × 37 = 111, that is 111 is a multiple of 3.

∴ 111 is divisible by 3.

Question 7: If there are 20 mangoes in a basket. How many mangoes will be there in 30 such baskets?

Number of mangoes in one basket = 20

Number of baskets = 30

Total number of mangoes in 30 baskets = 20 × 30 = 600.

Therefore, there are 600 mangoes in 30 baskets.

Question 8: Which of the following is not a multiple of 23?

Now, 23 × 6 = 138, 23 × 8 = 184 and 23 × 11 = 253, so clearly 254 is not a multiple of 23.

(c) is the answer.

Question 9: 72 books are kept on a bookshelf with 8 shelves. If each shelf has the same number of books. Find the number of books on each shelf.

Total number of books = 72

Number of shelves = 8

Now, 8 × 9 = 72

Therefore, there are 9 books on each shelf.

Question 10: Arifa daily practices 5 maths sums. How many sums did she solve in the month of July?

Number of questions she daily solves = 5

Number of days in July = 31

Total number of questions = 31 × 5 = 155

Therefore, she solved 155 questions in the month of July.

Video Lesson on Common Multiples and Its Applications

Practice Questions on Multiples

1. Find the first five multiples of 13.

2. Find the first three common multiples of 6 and 18.

3. Find the lowest common multiple of 2, 14, and 16.

4. Niya ate 4 chocolates every day for a week. How many total chocolates did she eat?

5. List all the numbers whose multiple is 286.

Keep visiting BYJU’S to get more such study materials explained in an easy and concise way. Also, register now and get access to 1000+ hours of video lessons on different topics.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Multiples Worksheets

Multiples Between

First 5 Multiples

Even Multiples

Groups of Numbers

Three Common Multiples

Missing Multiples

Color Grids

Visual Multiples

Multiple Choice

Cross Out All

Rows of Multiples

Multiple Matrix

In the Times Table Worksheet

About these 15 worksheets.

Imagine you’re standing at the base of a staircase. Each step you take moves you up by the same number of stairs, and as you continue, the ascent becomes predictable, methodical. This pattern of adding a fixed number of steps mirrors the mathematical concept of “multiples.” It’s a simple yet fundamental idea: the process of repeatedly adding the same number to itself. Though the term “multiples” may initially seem technical, at its core, it’s about consistent repetition-whether adding 3s, 5s, or any number-and climbing higher with each step. To make learning this essential skill more accessible and engaging, educators have created tools like multiples worksheets, which provide structured, interactive ways to grasp the concept.

Multiples are deeply embedded in the fabric of mathematics. To illustrate, think of the number 3. If you continuously add 3 to itself-3, 6, 9, 12, and so on-you generate a series of multiples of 3. These numbers are nothing more than results of adding 3 over and over, much like hopping up that staircase. But while this process is simple to understand, developing a strong familiarity with it requires practice, and that’s where multiples worksheets become invaluable. These worksheets serve as essential practice grounds, providing opportunities for learners to repeat and reinforce their understanding of multiples in a variety of contexts.

When you first dive into these worksheets, you’ll encounter exercises designed to introduce and solidify the basics. One such exercise might ask you to list the first ten multiples of a given number, say 5. Through this type of straightforward practice, you internalize the process of repeated addition, recognizing patterns as you go. By regularly engaging in these problems, you begin to understand multiples not just as an abstract mathematical term, but as a predictable, manageable concept that builds on itself.

As you progress, the worksheets introduce more advanced challenges, prompting deeper thinking and greater problem-solving skills. For instance, a task might present you with a group of numbers and ask which ones are multiples of 7. This type of exercise shifts the focus from generating multiples to recognizing them, honing your ability to discern patterns and identify relationships between numbers. These problems cultivate analytical thinking, teaching you to sift through information and spot the right connections, an essential skill in more advanced mathematical areas.

Word problems also make frequent appearances in multiples worksheets, adding an element of real-world application to the concept. Consider a problem like, “Sarah buys 4 candies every day. How many candies will she have after a week?” By applying your understanding of multiples, you can easily determine that after seven days, Sarah will have 28 candies (7 days × 4 candies per day). This type of exercise illustrates how multiples aren’t just abstract numbers on a page, but practical tools that help solve everyday problems-from counting candies to planning schedules and budgets.

Another type of exercise you might encounter involves pattern recognition, an area where multiples play a starring role. A worksheet might give you a sequence of numbers with missing values and ask you to identify the missing numbers based on a given multiple. By recognizing the consistent pattern, you not only reinforce your understanding of multiples but also improve your ability to detect numerical patterns, a skill that becomes increasingly important in advanced mathematical topics like algebra and number theory. This kind of problem stretches your mind, encouraging logical reasoning and a deeper appreciation for the order hidden within numbers.

The benefits of working through multiples worksheets extend far beyond immediate problem-solving. At their core, these worksheets offer a structured way to practice thinking systematically and methodically. Each time you solve a problem, you strengthen your understanding of multiples, making them more intuitive. Over time, this repetitive practice sharpens your ability to recognize patterns and relationships between numbers, laying a strong foundation for more complex mathematical concepts, such as least common multiples (LCM), ratios, and proportions. With a solid grasp of multiples, you’ll be better prepared to tackle these more advanced topics with confidence and ease.

Multiples are not only crucial in the classroom-they appear throughout daily life. Take, for example, the world of music. When you listen to a song, you might tap your foot to the rhythm. That rhythm often follows predictable patterns based on multiples. The beat you’re tapping to may repeat every 4 or 8 counts, and understanding how multiples work can help you predict when the next beat will drop, enhancing your sense of timing and rhythm.

In other everyday situations, multiples are just as relevant. Imagine you’re planning a party and need to arrange chairs in rows of 8. Knowing how multiples work allows you to quickly calculate how many chairs you’ll need for, say, 5 rows (40 chairs in total). This concept ensures you have the correct number of chairs without leaving any extras or needing to scramble for more at the last minute.

Even grocery shopping involves multiples. Suppose each packet of cookies contains 10 cookies, and you purchase 3 packets. Using your understanding of multiples, you can easily calculate that you now have 30 cookies. In this way, multiples aren’t just mathematical exercises-they’re tools that simplify everyday tasks, from organizing events to managing your budget.

In sports, multiples can also be found in training routines. A basketball player might practice shooting by taking 15 shots in a set. If the player repeats this set 4 times, understanding multiples allows them to quickly determine they’ve taken 60 shots in total. This type of calculation not only helps athletes track their progress but also encourages discipline and structured practice.

What is a Multiple?

In mathematics, a multiple of a number is the product obtained when that number is multiplied by an integer. Simply put, if you have a number a and you multiply it by any integer, the result is a multiple of a. For example, the multiples of 3 are found by multiplying 3 by different integers, such as 3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, and so on. Multiples can be positive, negative, or zero depending on the integer used in the multiplication. It’s important to note that every number is a multiple of itself because multiplying a number by 1 yields the number itself.

Characteristics of Multiples

One key feature of multiples is that they continue infinitely. This is because there are an infinite number of integers to multiply by. For any number a, there is no limit to how large or small its multiples can be. Moreover, all multiples of a given number are evenly divisible by that number. For example, any multiple of 5 is divisible by 5 without leaving a remainder. This property helps in solving problems involving divisibility, common multiples, and greatest common divisors.

Example 1: Multiples of 4

Let’s take 4 as an example. The multiples of 4 are obtained by multiplying 4 by 1, 2, 3, 4, etc. So, the multiples of 4 are:

These multiples go on indefinitely. Each of these numbers can be divided by 4, confirming that they are indeed multiples. Additionally, if we consider negative integers, the multiples of 4 can also include negative numbers like 4 x -1 = -4, 4 x -2 =-8 and so on.

Example 2: Multiples of 7

Let’s consider the number 7. To find its multiples, we multiply 7 by positive and negative integers. The first few multiples of 7 are:7 x 1=7,7 x 2=14,7 x 3=21,7 x 4=28,7 x 5=35

As with 4, the multiples of 7 extend infinitely in both positive and negative directions. For instance, 7 x -1 = -7 and 7 x -2 = -14. Again, each of these multiples is divisible by 7.

Common Multiples

Sometimes, we are interested in the multiples that two or more numbers share. These are called common multiples. For instance, 4 and 6 have common multiples because some numbers, like 12 and 24, are multiples of both. Finding the least common multiple (LCM) of two numbers can help solve problems related to synchronization or matching quantities, like when two events need to occur at the same time in periodic intervals.

multiples Worksheets

• Kindergarten

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Understanding multiplication

Here you will learn about multiples, including how to calculate multiples of a number and solve problems using knowledge of multiples.

Students will first learn about multiples as part of operations and algebraic thinking in elementary school.

What are multiples?

Multiples are the products you get when two numbers, or factors, are multiplied.

For example, the first five multiples of 7 are 7 , 14 , 21 , 28 , and 35 .

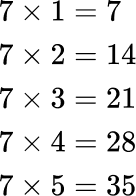
You can skip count on a number line to find multiples of 7 .

The number line shows the first 7 multiples of 7 , but you could keep skipping counting to find more multiples.

To make them easier to find, multiples of the numbers 1 to 9 have patterns. They can help you decide if a given number is a multiple of 1 to 9 .

Common Core State Standards

How does this relate to 4th grade math?

• 4th Grade: Operations and Algebraic Thinking (4.OA.B.4) Determine whether a given whole number in the range 1 to 100 is a multiple of a given one-digit number.

How to identify multiples

In order to find if a number is a multiple of another number:

• Think about the pattern for the multiples of the number.

Decide if the number is a multiple.

[FREE] Multiples Worksheet (Grade 4)

Use this worksheet to check your grade 4 students’ understanding of multiples. 15 questions with answers to identify areas of strength and support!

Multiples examples

Example 1: decide whether a number is a multiple.

Is 76 a multiple of 6 ?

• Think about the pattern for the multiples of the number. 

Start a list of multiples for 6 :

6 , 12 , 18 , 24 , 30 …

Notice that the multiples of 6 are also multiples of 2 and 3 .

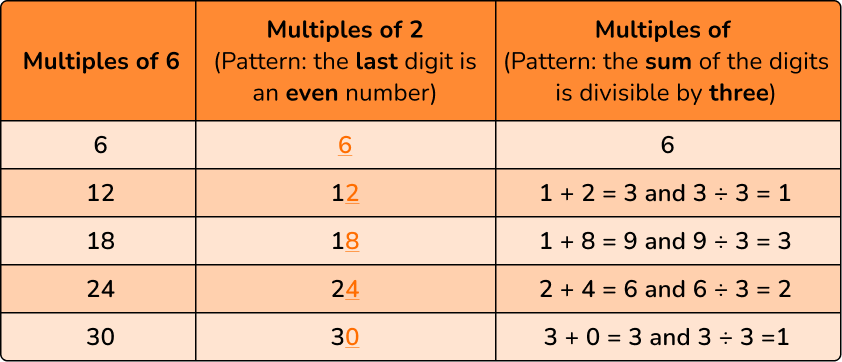
This pattern is true for all multiples of 6 .

2 Decide if the number is a multiple .

✔ The last digit (6) is even, so it is a multiple of 2 .

✘ The sum of the digits (7 + 6 = 13) , so it is not a multiple of 3 .

76 is NOT a multiple of 6 because it is NOT a multiple of 3 .

Skip counting on a number line shows that 76 is NOT a multiple of 6 .

Example 2: decide whether a number is a multiple

Is 65 a multiple of 5 ?

Think about the pattern for the multiples of the number .

Start a list of multiples for 5 :

5 , 10 , 15 , 20 , 25 …

Notice that they end in either a 5 or a 0 .

This pattern is true for all multiples of 5 .

✔ 65 is a multiple of 5 because it ends in a 5 .

Skip counting on a number line shows that 65 is the 13^{th} multiple of 5 .

Example 3: decide whether a number is a multiple

Is 66 a multiple of 4 ?

Start a list of multiples for 4 :

4 , 8 , 12 , 16 , 20 …

Notice that they are all doubles of a multiple of 2 .

This pattern is true for all multiples of 4 .

✘ 66 is the double of 33 \rightarrow 33 \times 2=66 , but 33 is not a multiple of 2 .

66 is not a multiple of 4 because it is not a double of a multiple of 2 .

Skip counting on a number line shows that 66 is NOT a multiple of 4 .

Example 4: decide whether a number is a multiple

Is 72 a multiple of 9 ?

Start a list of multiples for 9 :

9 , 18 , 27 , 36 , 45 …

Notice that the sum of the digits is divisible by 9 .

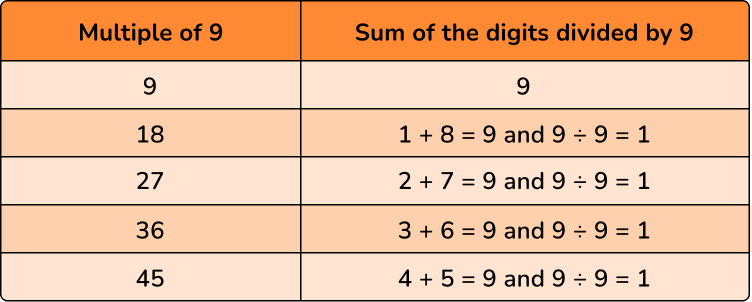
This pattern is true for all multiples of 9 .

✔ 72 is a multiple of 9 , because the sum of the digits (7+2=9) is divisible by 9 .

Skip counting on a number line shows that 72 is the eighth multiple of 9 .

Example 5: decide whether a number is a multiple

Is 42 a multiple of 3 ?

Start a list of multiples for 3 :

3 , 6 , 9 , 12 , 15 …

Notice that the sum of the digits is divisible by 3 .

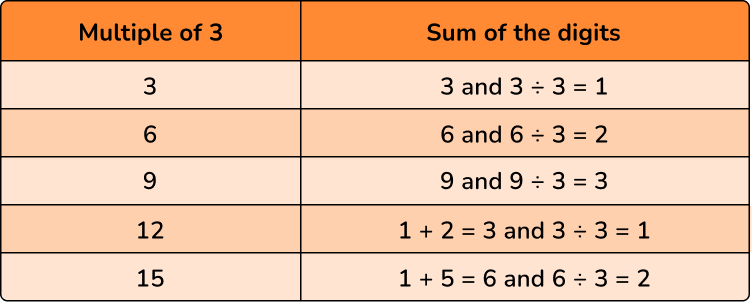
This pattern is true for all multiples of 3 .

✔ 42 is a multiple of 3 , because the sum of the digits (4+2=6) is divisible by 3 .

Skip counting on a number line shows that 42 is the 14^{th} multiple of 3 .

Example 6: decide whether a number is a multiple

An elementary school is performing a play. They want to put out 88 chairs for the audience. If they want the same amount of chairs in each row, should they do rows of 6 , 8 or 10 ?

Multiples of 6 : the sum of the digits is divisible by three.

Multiples of 8 : the number is double a multiple of 4 .

Multiples of 10 : the last digit is zero.

✘ 88 is NOT a multiple of 6 , because the sum of the digits (8 + 8 = 16) is NOT divisible by 3 .

✔ 88 is a multiple of 8 , because it is double a multiple of 4 \rightarrow 2 \times 44=88 .

The school should put the 88 chairs in rows of 8 .

Teaching tips for multiples

• Use a multiplication table so that students can see examples of multiples and look for patterns.
• While students will need to remember the multiple patterns to solve quickly, avoid just using math worksheets. Help students deepen their understanding and likelihood of remembering by also doing hands-on activities. For example, give students 52 counters and ask them to make as many arrays as possible to find out what factors 52 is a multiple of.
• Play games regularly to help students memorize larger multiples. For example, have students count starting from 1 (the first student says 1 , the second says 2 , the third says 3 and so on), but challenge them to use a different word for a certain multiple each time. So if they were playing with multiples of 7 , whenever a student got to a multiple of 7 , they would say “cookie” instead of the multiple.

Easy mistakes to make

• Confusing the terms multiples and factors Factors and multiples are easily mixed up. Remember multiples are the numbers in the middle of the multiplication table, whereas factors are the numbers around the outside (the numbers being multiplied).

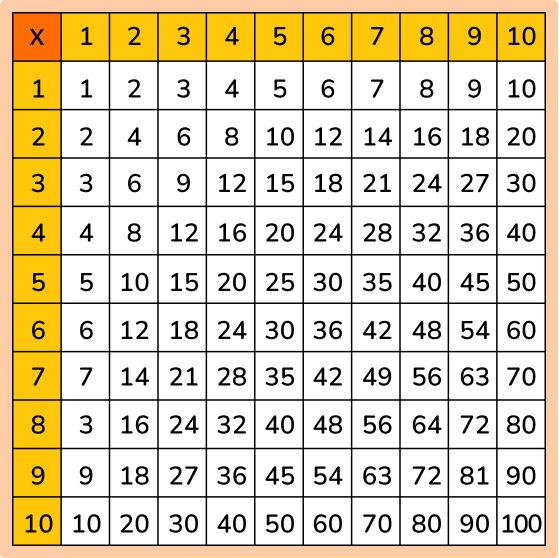
• Forgetting the number itself as a multiple All numbers are a multiple of themselves. For example, the multiples of 6 are: 6 , 12 , 18 , 24 and so on and so 6 is a multiple of itself.

Related lessons on factors and multiples

• Factors and multiples
• Least common multiple
• Greatest common factor
• Factor tree
• GCF and LCM
• Prime factors
• Factor pairs

Practice multiples questions

1. Which number is a multiple of 2 ?

For multiples of 2 , the last digit is an even number. 54 ends in an even number and 27 \times 2=54 , so 54 is a multiple of 2 .

2. Which number is a multiple of 7 ?

Using a number line to skip count by 7 , shows that 91 is a multiple of 7 .

3. Which number is NOT a multiple of 3 ?

For multiples of 3 , the sum of the digits is divisble by three. 4+3=7 is not divisible by 3 , so 43 is NOT a multiple of 3 .

4. Which number is NOT a multiple of 4 ?

For multiples of 4 , the number is double a multiple of 2 . 58 is the double of 29 , so 58 is NOT a multiple of 4 .

5. A grocery store has 78 boxes of cereal. They want to put the same number of boxes on each shelf. How many boxes should they put on each shelf?

For multiples of 6 , the number is divisible by both two and three. 78 is a multiple of 2 , because it ends in an even number (8) . 78 is a multiple of 3 , because 7 + 8 = 15 and 15 \div 3 = 5 .

So 78 is a multiple of 6 \rightarrow 6 \times 13=78 The grocery store can put 6 boxes on each shelf.

Multiples FAQs

Times tables are a list of multiplication equations for a certain number and include both factors and multiples. Multiples are the answers (products) in times tables.

Yes, if a number divides another number without a remainder, it’s a multiple. For example, in the question “is 72 a multiple of 2 ?” you can solve 72 \div 2=36 . There are no remainders, so it is a multiple.

All positive and negative numbers have multiples. However, in 4th grade math you only work with positive numbers.

Prime numbers have an infinite amount of multiples but only 2 factors.

The next lessons are

• Converting fractions, decimals and percentages
• Fractions operations

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

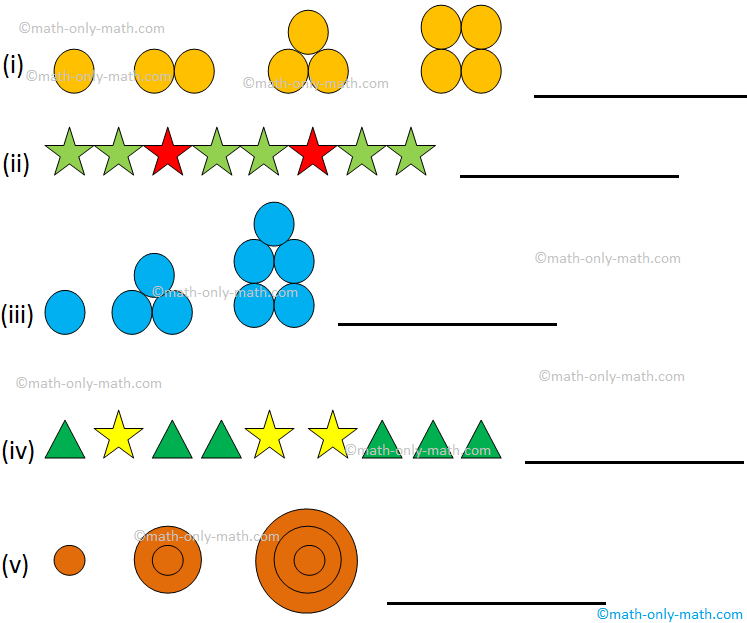
Examples on Multiples

Examples on multiples on different types of questions on multiples are discussed here step-by-step. Every number is a multiple of itself. Every number is a multiple of 1. Every multiple of a number is either greater than or equal to the number. Product of two or more numbers is a multiple of each of the numbers.

1.  Write the first three multiples of 11.

The first three multiples of 11 are: 

11 x 1 = 11,

11 x 2 = 22,

11 x 3 = 33,

Thus, the first three multiples of 11 are 11, 22 and 33. 

2. Write the first five multiples of 17. Solution: The first five multiples of 17 are: 17 x 1 = 17, 17 x 2 = 34, 17 x 3 = 51, 17 x 4 = 68, 17 x 5 = 85 Thus, the first five multiples of 17 are 17, 34, 51, 68 and 85.

3. Is 72 is a multiple of: (i) 9 (ii) 6 Solution: (i)

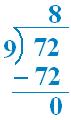
So, 72 = 8 × 9 Thus, 72 is a multiple of 9. (ii)

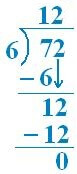
So, 72 = 6 × 12 Thus, 72 is a multiple of 6.

4. Is 85 a multiple of 9? Solution:

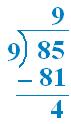
Thus, 9 is not a factor of 85. So, 85 is not a multiple of 9.

5. Write the first five multiples of 21. Solution: The first five multiples of 21 are: 21 x 1 = 21, 21 x 2 = 42, 21 x 3 = 63, 21 x 4 = 84, 21 x 5 = 105 Thus, the first five multiples of 21 are 21, 42, 63, 84 and 105. Students can practice these five examples on multiples which are discussed here step-by-step.

Related Concept

● Factors and Multiples by using Multiplication Facts

● Factors and Multiples by using Division Facts

● Multiples

● Properties of Multiples

● Examples on Multiples

● Factor Tree Method

● Properties of Factors

● Examples on Factors

● Even and Odd Numbers

● Even and Odd Numbers Between 1 and 100

● Examples on Even and Odd Numbers

4th Grade Math Activities From Examples on Multiples to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

2nd Grade Data Handling | Collection of Objects |Information Collected

Dec 16, 24 02:16 PM

Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns

Dec 15, 24 10:27 AM

2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line

Dec 14, 24 02:12 PM

2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic

Dec 14, 24 12:25 PM

Patterns in Math | Missing Number | Counting Numbers | Worksheets

Dec 13, 24 12:31 AM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• Practice Questions

Discover the fascinating world of multiples in mathematics with our comprehensive guide. Ideal for educators, students, and math enthusiasts, this article demystifies the concept of multiples through clear explanations and engaging examples. Whether you’re tackling homework, preparing for exams, or just curious about math, our guide provides the insights you need. Dive into the world of multiples and enhance your mathematical understanding today.

What are Multiples in Maths?

Multiples in maths are the result of multiplying a number by an integer. Simply put, when you take any number and multiply it by 1, 2, 3, 4, and so on, the products you get are known as the multiples of that number. For instance, the multiples of 3 include 3 (3×1), 6 (3×2), 9 (3×3), 12 (3×4), and continue in this pattern. Essentially, multiples are what you count by when you skip count by a particular number, making them a fundamental concept in both arithmetic and algebra.

let’s a look of few examples here.

Multiples of 2:  2, 4, 6, 8, 10, 12, 14, 16, 18, 20

Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30

Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40

Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50

Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60

Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70

Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80

Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90

Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 ​

Properties of Multiples

Understanding the properties of multiples is crucial for grasping how numbers interact within the mathematical universe. These properties not only simplify computations but also enable us to recognize patterns and solve problems more efficiently. Here, we delve into the fundamental characteristics that define the nature of multiples.

1. Infinite Occurrence

One of the most intriguing aspects of multiples is their infinite nature. For any given number, there exists an endless series of multiples. This is because you can keep multiplying the number by increasingly larger integers, extending the series indefinitely. For example, the multiples of 2 (2, 4, 6, 8, 10…) continue endlessly as you multiply 2 by larger numbers.

2. Zero as a Multiple

A lesser-known fact is that zero (0) is considered a multiple of every number. This is due to the property that any number multiplied by zero equals zero. Hence, zero uniquely stands as a universal multiple, underscoring the foundational role it plays in mathematics.

3. Divisibility

A number is a multiple of another if it can be divided by that number without leaving a remainder. This property of divisibility is fundamental to understanding multiples. For instance, 15 is a multiple of 3 and 5 because it can be divided evenly by these numbers (15 ÷ 3 = 5).

4. Common Multiples

When two or more numbers share a multiple, it is known as a common multiple. The least common multiple (LCM) is particularly important in various mathematical operations, especially in solving fractions and equations. The LCM of two numbers is the smallest number that is a multiple of both.

5. Multiples and Prime Numbers

Prime numbers, which are numbers greater than 1 that have no divisors other than 1 and themselves, have a unique relationship with multiples. Each prime number’s multiples are exclusively generated by multiplying the prime number by integers. For example, the multiples of 5 are all the numbers that can only be obtained by multiplying 5 by an integer.

6. Pattern Recognition

Multiples often form recognizable patterns, which can be particularly helpful in mental math and problem-solving. For example, the multiples of 2 always end in 0, 2, 4, 6, or 8, reflecting the pattern of even numbers. Similarly, the multiples of 5 end in either 0 or 5. Recognizing these patterns can simplify computations and enhance number sense.

How to Find Multiples of a Number

A multiple of a number is  a number that is the product of a given number and some other natural number. Finding multiples of a number is a fundamental skill in mathematics that lays the groundwork for more complex operations and concepts. This guide will walk you through the steps to identify multiples, enhancing your mathematical proficiency and understanding.

Understanding Multiples

Before diving into the process, it’s essential to grasp what multiples are. A multiple of a number is what you get when you multiply that number by an integer. Multiples are like the building blocks in the world of mathematics, forming patterns and sequences that are foundational to various mathematical concepts.

• Start with the Number : Begin by choosing the number for which you want to find multiples. This number is your base or starting point.
• Multiply by Integers : The simplest way to find multiples is to multiply your chosen number by integers (whole numbers). Start with 1, then 2, 3, 4, and so on. For example, if you’re finding multiples of 3, you’ll multiply 3 by 1 to get 3, by 2 to get 6, by 3 to get 9, and continue this pattern.
• List the Products : As you multiply, list down the products. These products are the multiples of your chosen number. Continuing with the example of 3, your list will start with 3, 6, 9, 12, 15, and so on.
• Recognize Patterns : As you list the multiples, you might start to notice patterns. For instance, multiples of 2 always end in 0, 2, 4, 6, or 8, while multiples of 5 end in 0 or 5. Identifying these patterns can make finding multiples quicker and more intuitive.
• Use Multiplication Tables : If you’re familiar with multiplication tables, you can use them as a shortcut to find multiples. The row or column corresponding to your number in the table will list its multiples.
• Incorporate Technology : For larger numbers or for a more extensive list of multiples, consider using calculators or online tools. These can save time and ensure accuracy, especially when dealing with numbers outside the typical multiplication table range.

For this example, we’ve chosen the number 4.

We begin by multiplying 4 by integers (whole numbers) starting from 1. Here’s how it looks:

• 4 × 10 = 40

As we multiply, we list the products, which are the multiples of 4:  4, 8, 12, 16, 20, 24, 28, 32, 36, 40…

In this case, you might notice that all multiples of 4 are even numbers. This pattern can help you quickly identify multiples of 4, even without doing the multiplication explicitly.

List of Multiples

Difference Between Factors and Multiples

Common Multiples

In the mathematical landscape, the concept of common multiples plays a pivotal role in various arithmetic and algebraic operations. Understanding common multiples is essential for solving problems related to least common multiples (LCM), simplifying fractions, and finding solutions to equations involving multiple terms. This guide aims to shed light on what common multiples are, how to find them, and their practical applications, enhancing your mathematical toolkit.

Understanding Common Multiples

Common multiples of two or more numbers are multiples that the numbers share. These are numbers that can be divided evenly by all the original numbers without any remainder. For instance, if you’re considering the numbers 4 and 6, some of their common multiples would be 12, 24, 36, and so on. Each of these common multiples can be divided evenly by both 4 and 6.

Finding Common Multiples

• Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
• Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40…
• Identify Common Multiples : Look through the lists to find multiples that appear in all lists. In the example above, 12 and 24 are common multiples of 3 and 4.
• Least Common Multiple (LCM) : The smallest of the common multiples is known as the Least Common Multiple (LCM). For 3 and 4, the LCM is 12, as it is the smallest number that both 3 and 4 can divide into without a remainder.

Find the Multiples of 2?

The multiples of 2 represent the essence of even numbers. Each product in this series is a result of multiplying 2 by integers ranging from 1 to 10. This sequence is fundamental in mathematics, illustrating the basic concept of even numbers, which are divisible by 2 without any remainder. Understanding these multiples is crucial for grasping the properties of even numbers, which play a significant role in various arithmetic operations and number theory.

• 2 × 10 = 20

Find the Multiples of 3?

The table showcasing the multiples of 3 highlights a pattern where each number is divisible by 3. This series is particularly important for understanding the concept of divisibility and for identifying numbers that are multiples of 3. These multiples are integral to various mathematical concepts, including factors, multiples, and patterns within the number system. Recognizing the sequence of multiples of 3 aids in developing arithmetic skills and enhances problem-solving capabilities.

• 3 × 10 = 30

Find the Multiples of 4?

The multiples of 4 table demonstrates how numbers increase when multiplied by 4. Each step in this series doubles the even number sequence, further emphasizing the structure within the number system. This table is useful for understanding the multiplication process and for recognizing patterns associated with the number 4. It serves as a valuable tool for students learning basic multiplication and for anyone working with numbers divisible by 4.

Find the Multiples of 5?

he multiples of 5 are easily recognizable by their ending digits, either 0 or 5. This pattern is not only simple to remember but also crucial for various arithmetic calculations, especially in mental math. The table of multiples of 5 is particularly useful in real-world applications, such as counting by fives, dealing with currency, and measuring time

• 5 × 10 = 50

Find the Multiples of 6?

The table of multiples of 6 combines the properties of even numbers and the divisibility by 3. This series is essential for understanding more complex patterns in the number system and for solving problems related to least common multiples and divisibility.

• 6 × 10 = 60

In conclusion, multiples form an essential part of mathematics, offering a foundation for understanding arithmetic patterns and solving complex problems. By mastering the concept of multiples and recognizing their patterns, learners can enhance their mathematical skills, facilitating easier computation and a deeper comprehension of numerical relationships, crucial for academic success and daily applications.

AI Generator

Text prompt

• Instructive
• Professional

school Ready to Test Your Knowledge?

Before you leave, take our quick quiz to enhance your learning!

Filter year:

Multiples of 2 Reasoning and Problem Solving

Consolidate numbers in the 2 times table knowledge by downloading our Year 3 Multiples of 2 reasoning and problem solving worksheet. We have created three different types of reasoning and problem solving questions with two of each for your children to tackle and flex their multiplication knowledge!

Perfect for an independent learning task following a range of varied fluency questions or use in a small group as a discussion activity. A handy answer sheet has been provided to aid marking or encourage peer or self marking to save you time too.

Curriculum Objectives

• Count in steps of 2, 3, and 5 from 0, and in tens from any number, forward or backward
• Recall and use multiplication and division facts for the 2, 5 and 10 multiplication tables, including recognising odd and even numbers

Multiplication and Division

More like this

More Y3 resources

What are the multiples of 2 [SOLVED]

2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98

• Is 2 a composite number?
• Is 2 an even number?
• Is 2 an irrational number?
• Is 2 an odd number?
• Is 2 a perfect number?
• Is 2 a perfect square?
• Is 2 a prime number?
• Is 2 a rational number?
• What are the factors of 2?
• What is the prime factorization of 2?

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.