world in data representation

Population Growth

Explore global and country data on population growth, demography, and how this is changing.

By: Hannah Ritchie , Lucas Rodés-Guirao , Edouard Mathieu , Marcel Gerber , Esteban Ortiz-Ospina , Joe Hasell and Max Roser

Population growth is one of the most important topics we cover at Our World in Data .

For most of human history, the global population was a tiny fraction of what it is today. Over the last few centuries, the human population has gone through an extraordinary change. In 1800, there were one billion people. Today there are more than 8 billion of us.

But after a period of very fast population growth, demographers expect the world population to peak by the end of this century.

On this page, you will find all of our data, charts, and writing on changes in population growth. This includes how populations are distributed worldwide, how this has changed, and what demographers expect for the future.

Key insights on Population Growth

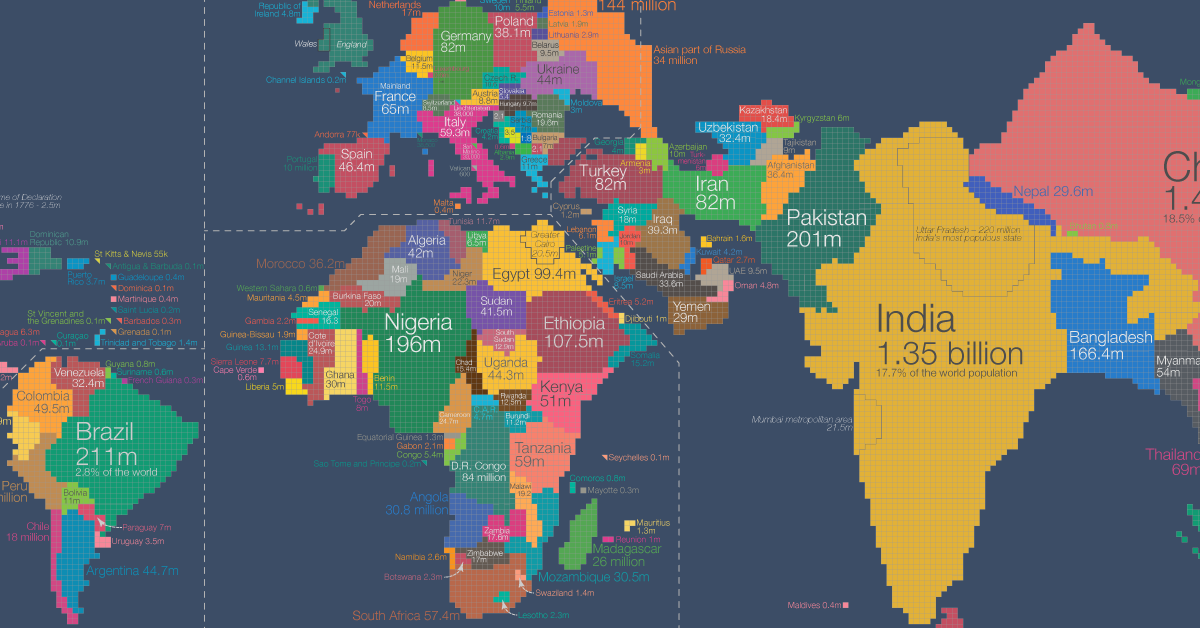
Population cartograms show us where the world’s people are.

Geographical maps show us where the world's landmasses are; not where people are. That means they don't always give us an accurate picture of how global living standards are changing.

One way to understand the distribution of people worldwide is to redraw the world map – not based on the area but according to population.

This is shown here as a population cartogram : a geographical presentation of the world where the size of countries is not drawn according to the distribution of land but by the distribution of people. It’s shown for the year 2018.

As the population size rather than the territory is shown in this map, you can see some significant differences when you compare it to the standard geographical map we’re most familiar with.

Small countries with a high population density increase in size in this cartogram relative to the world maps we are used to – look at Bangladesh, Taiwan, or the Netherlands. Large countries with a small population shrink in size – look for Canada, Mongolia, Australia, or Russia.

You can find more details on this cartogram in our article about it:

The map we need if we want to think about how global living conditions are changing

By showing us where the people in the world are, cartograms help us understand global living conditions better.

What you should know about this data

• This map is based on the United Nation’s 2017 World Population Prospects report. Our interactive charts show population data from the most recent UN revision. This means there may be minor differences between the figures shown on the map and the latest estimates in our other charts.

The world population has increased rapidly over the last few centuries

The speed of global population growth over the last few centuries has been staggering. For most of human history, the world population was well under one million. 1

As recently as 12,000 years ago, there were only 4 million people worldwide.

The chart shows the rapid increase in the global population since 1700.

The one-billion mark wasn’t broken until the early 1800s. It was only a century ago that there were 2 billion people.

Since then, the global population has quadrupled to eight billion.

Around 108 billion people have ever lived on our planet. This means that today’s population size makes up 6.5% of the total number of people ever born. 2

This increase has been the result of advances in living conditions and health that reduced death rates – especially in children – and increases in life expectancy.

See the data in our interactive visualization

• This data comes from a combination of sources, all detailed in our sources article for our long-term population dataset.

Population growth is no longer exponential – it peaked decades ago

There’s a popular misconception that the global population is growing exponentially. But it’s not.

While the global population is still increasing in absolute numbers, population growth peaked decades ago.

In the chart, we see the global population growth rate per year. This is based on historical UN estimates and its medium projection to 2100.

Global population growth peaked in the 1960s at over 2% per year. Since then, rates have more than halved, falling to less than 1%.

The UN expects rates to continue to fall until the end of the century. In fact, towards the end of the century, it projects negative growth, meaning the global population will shrink instead of grow.

Global population growth, in absolute terms – which is the number of births minus the number of deaths – has also peaked. You can see this in our interactive chart:

Annual population growth

The world has passed "peak child"

Hans Rosling famously coined the term " peak child " for the moment in global demographic history when the number of children stopped increasing.

According to the UN data, the world has passed "peak child", which is defined as the number of children under the age of five.

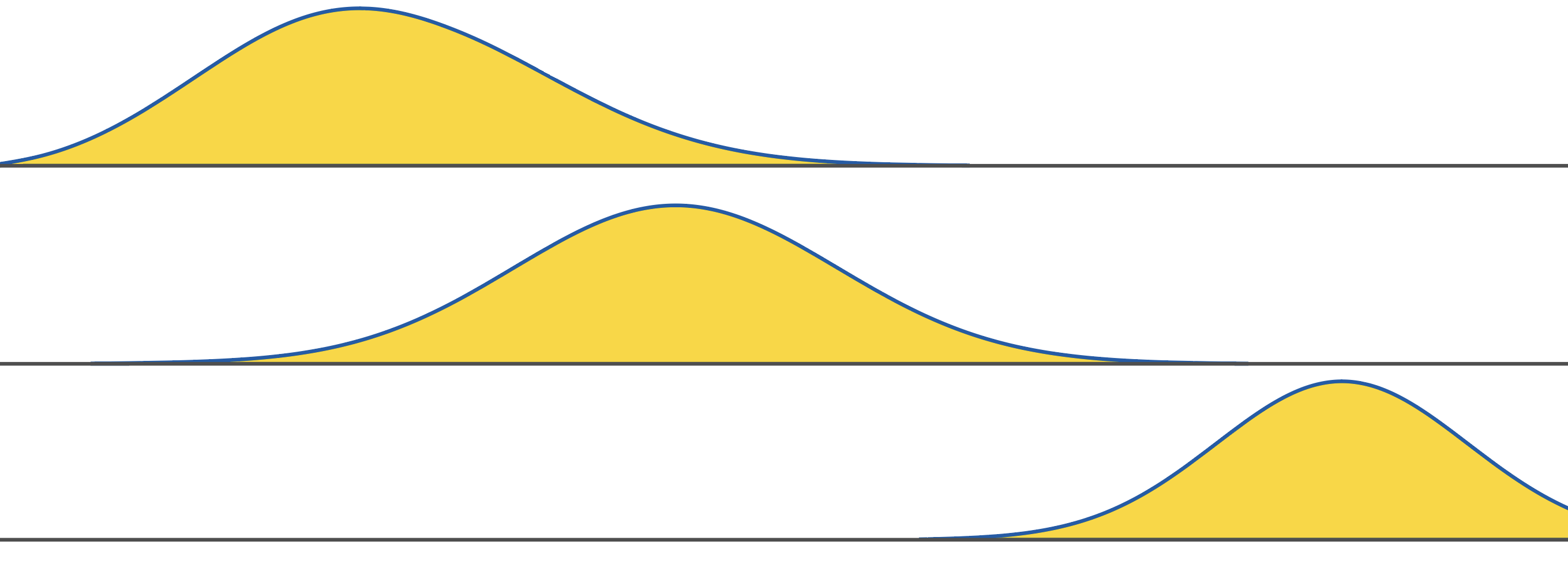
The chart shows the UN’s historical estimates and projections of the number of children under five.

It estimates that the number of children in the world peaked in 2017. For the coming decades, demographers expect a decades-long plateau before the number will decline more rapidly in the second half of the century.

• These projections are sensitive to the assumptions made about future fertility rates worldwide. Find out more from the UN World Population Division .
• Other sources and scenarios in the UN’s projections suggest that the peak was reached slightly earlier or later. However, most indicate that the world is close to "peak child" and the number of children will not increase in the coming decades.
• The 'ups and downs' in this chart reflect generational effects and 'baby booms' when there are large cohorts of women of reproductive age, and high fertility rates. The timing of these transitions varies across the world.

The UN expects the global population to peak by the end of the century

When will population growth come to an end?

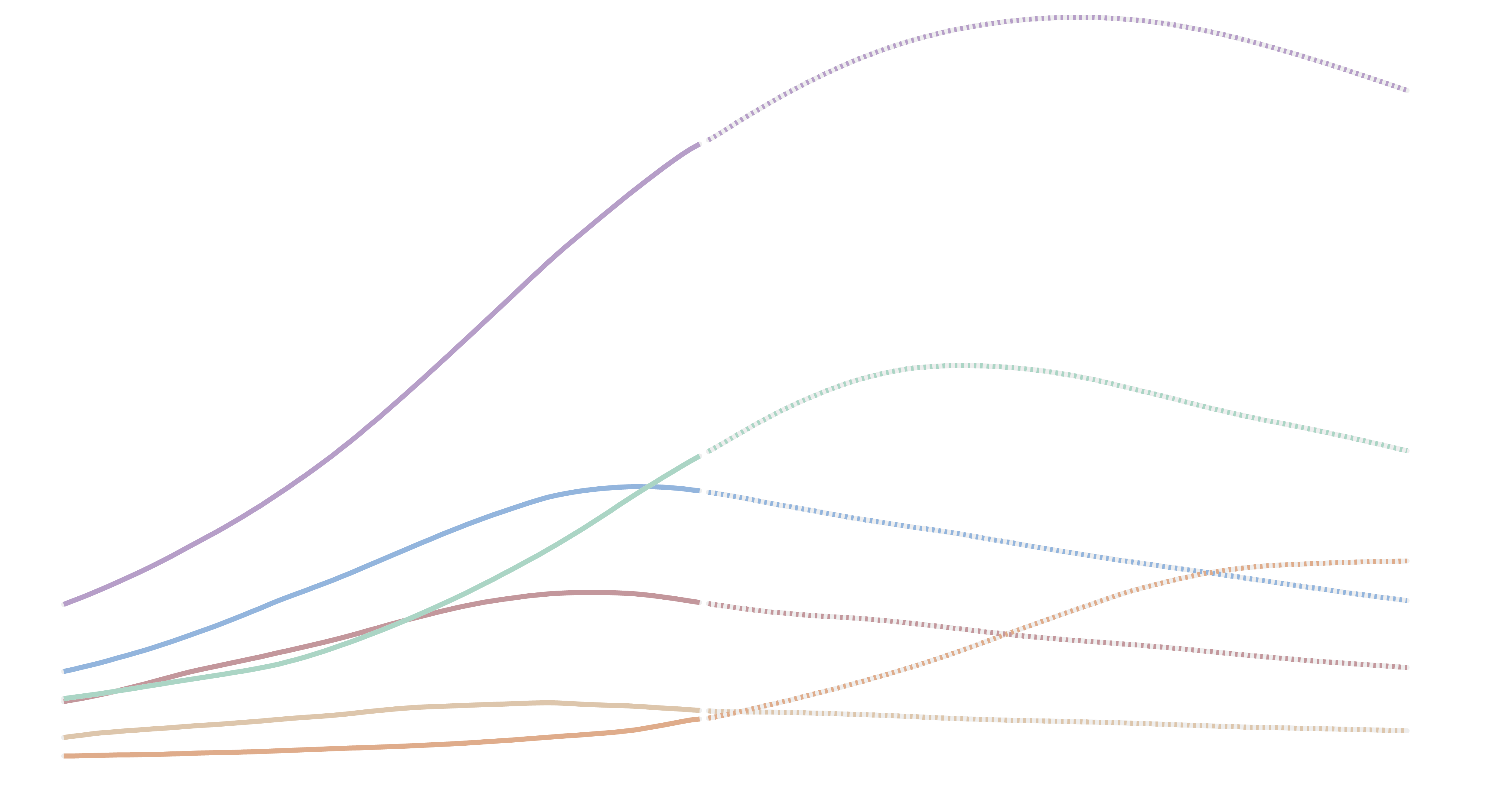
The UN’s historical estimates and latest projections for the global population are shown in the chart.

The UN projects that the global population will peak before the end of the century – in 2086, at just over 10.4 billion people.

• These projections are sensitive to the assumptions made about future fertility and mortality rates worldwide. Find out more from the UN World Population Division .
• Other sources and scenarios in the UN’s projections can produce a slightly earlier or later peak. Most demographers, however, expect that by the end of the century, the global population will have peaked or slowed so much that population growth will be small.

Explore data on Population Growth

Research & writing.

What would the work look like if each country's area was in proportion to its population?

How has world population growth changed over time?

The world population has increased rapidly in recent centuries. But this is slowing.

Max Roser and Hannah Ritchie

Demographic change

Two centuries of rapid global population growth will come to an end

India's population growth will come to an end: the number of children has already peaked

Hannah Ritchie

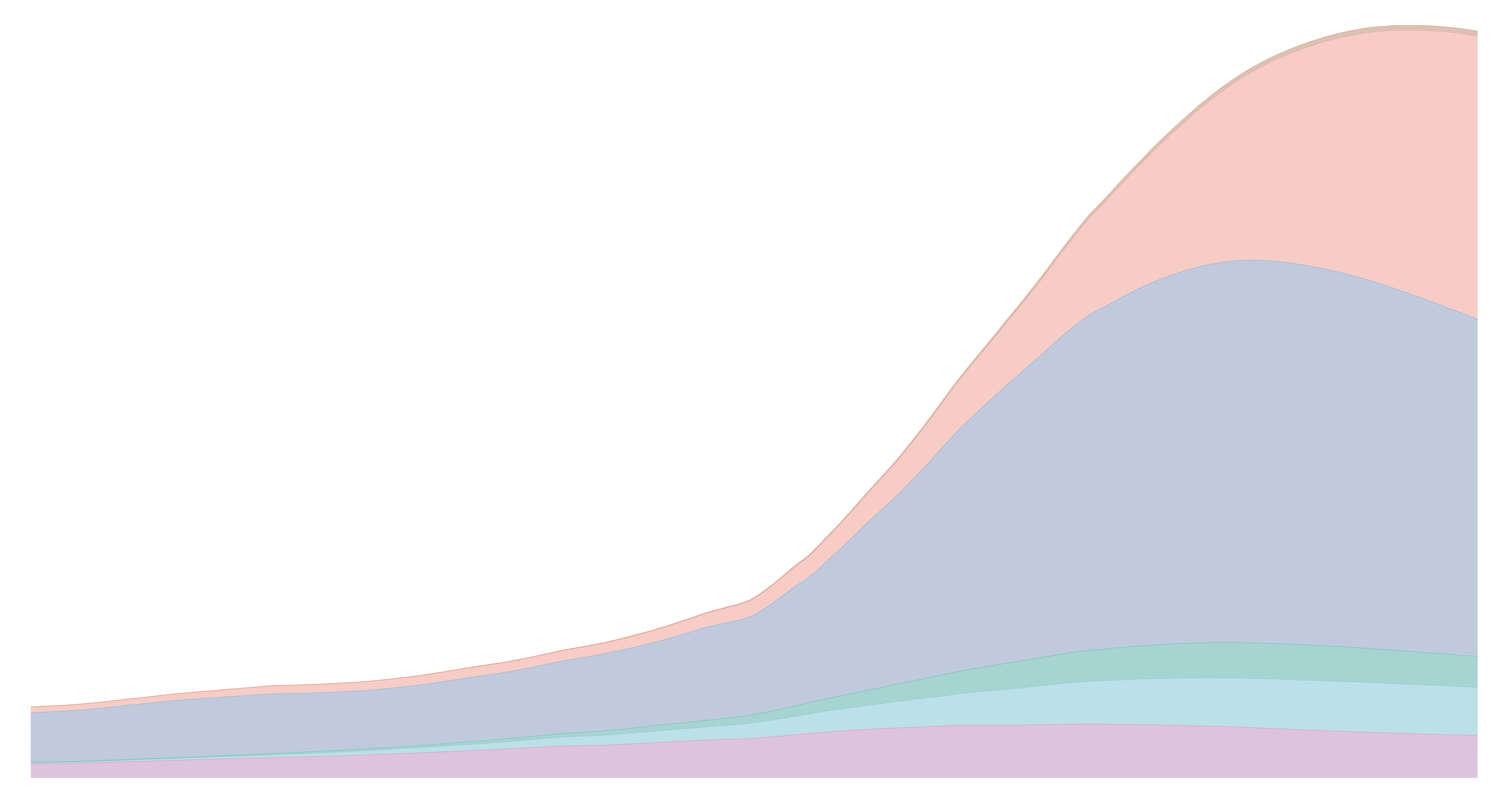
More than 8 out of 10 people in the world will live in Asia or Africa by 2100

The global population pyramid: How global demography has changed and what we can expect for the 21st century

Population momentum: If the number of children per woman is falling, why is the population still increasing?

Demographic transition: Why is rapid population growth a temporary phenomenon?

Definitions and sources.

What are the sources for Our World in Data’s population estimates?

Edouard Mathieu and Lucas Rodés-Guirao

The UN has made population projections for more than 50 years – how accurate have they been?

Other articles related to population growth.

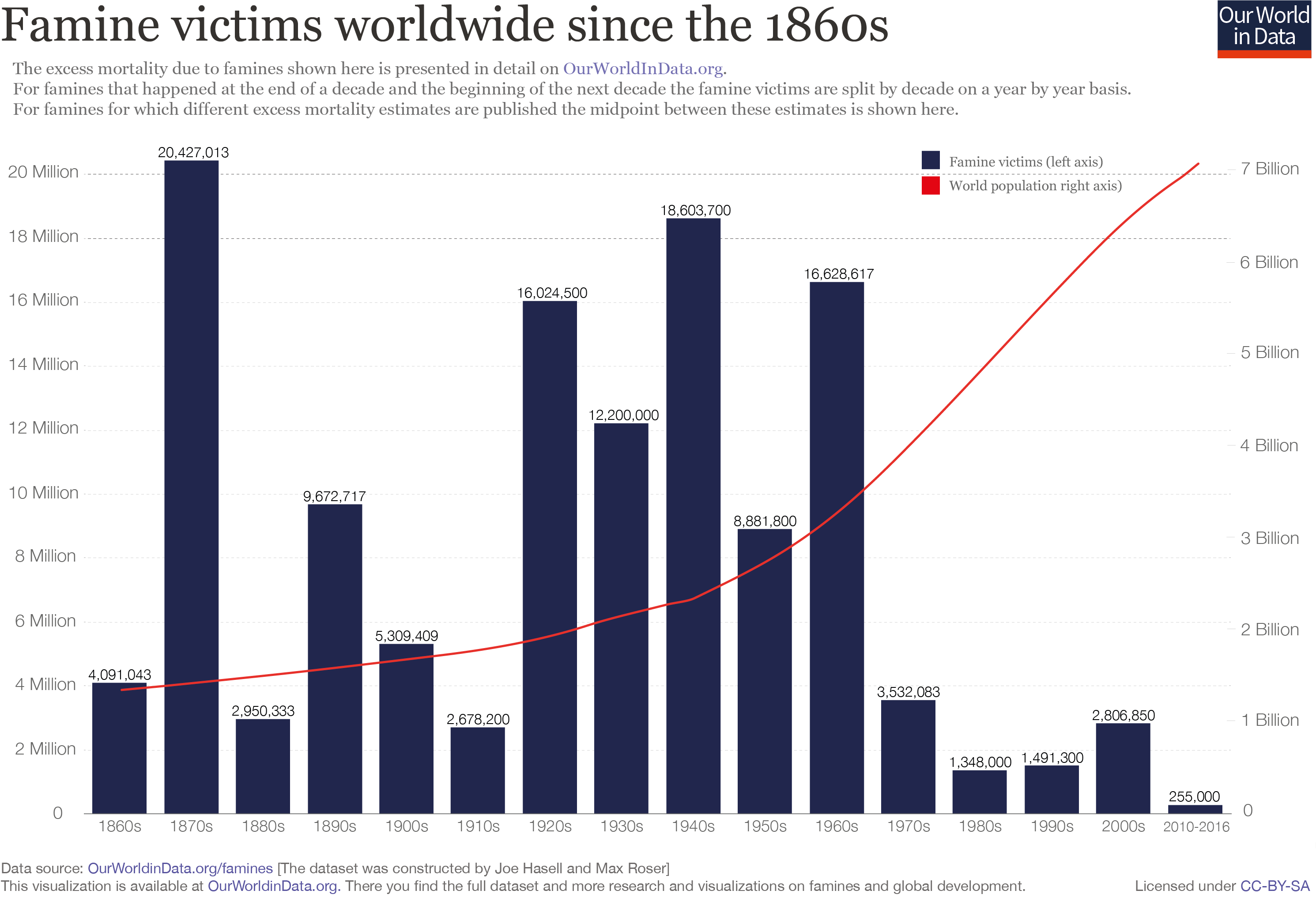
Does population growth lead to hunger and famine?

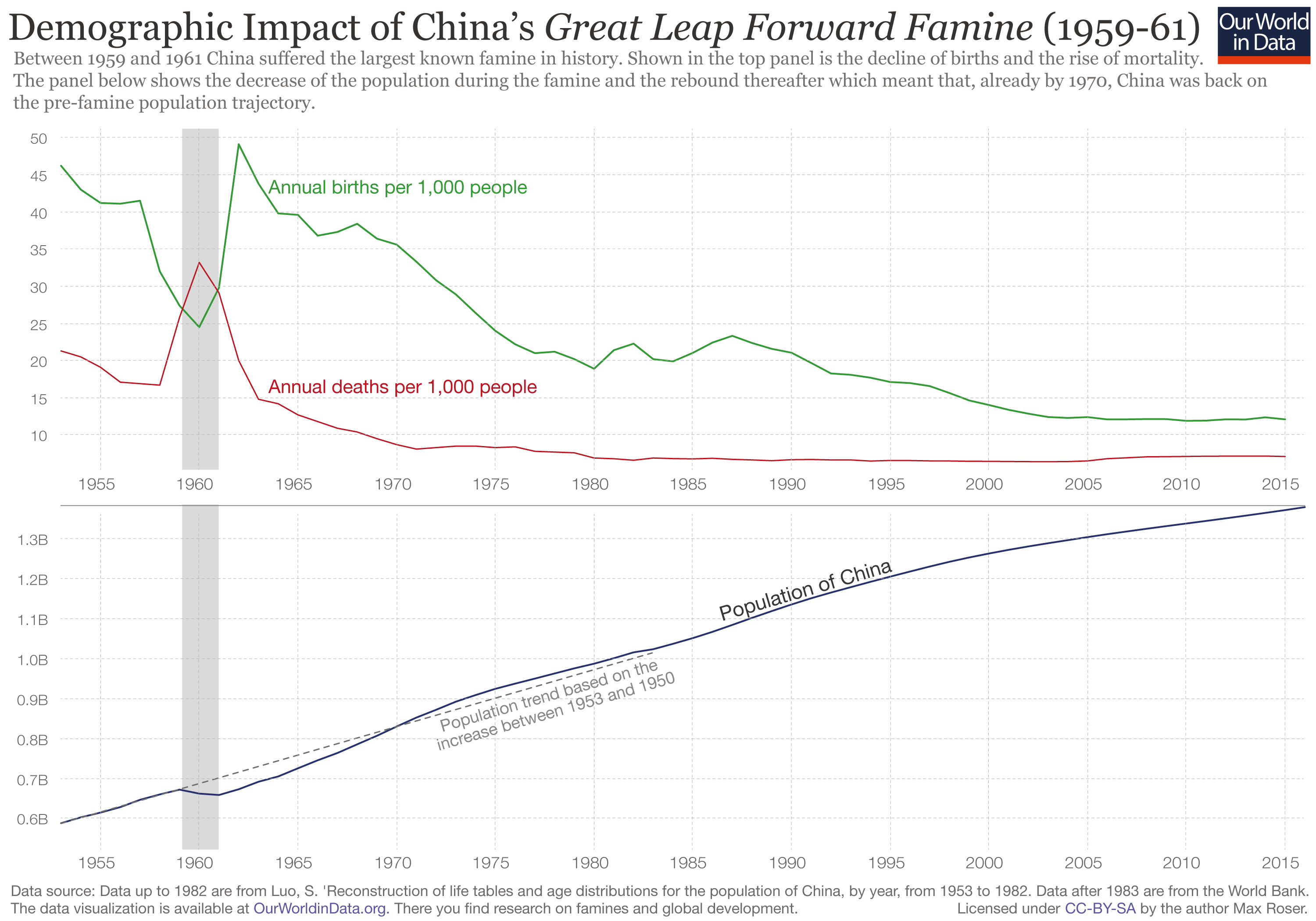
Do famines curb population growth?

More key articles on population growth, how many people die and how many are born each year.

Hannah Ritchie and Edouard Mathieu

Five key findings from the 2022 UN Population Prospects

Hannah Ritchie and Edouard Mathieu and Lucas Rodés-Guirao

Which countries are most densely populated?

Interactive charts on population growth.

See, for example, Kremer (1993) – Population growth and technological change: one million BC to 1990 . In the Quarterly Journal of Economics, Vol. 108, No. 3, 681-716.

As per 2011 estimates from Carl Haub (2011), “ How Many People Have Ever Lived on Earth? ” Population Reference Bureau.

Cite this work

Our articles and data visualizations rely on work from many different people and organizations. When citing this topic page, please also cite the underlying data sources. This topic page can be cited as:

BibTeX citation

Reuse this work freely

All visualizations, data, and code produced by Our World in Data are completely open access under the Creative Commons BY license . You have the permission to use, distribute, and reproduce these in any medium, provided the source and authors are credited.

The data produced by third parties and made available by Our World in Data is subject to the license terms from the original third-party authors. We will always indicate the original source of the data in our documentation, so you should always check the license of any such third-party data before use and redistribution.

All of our charts can be embedded in any site.

Our World in Data is free and accessible for everyone.

Help us do this work by making a donation.

Digital Humanities Data Curation

This is the first stop on your way to mastering the essentials of data curation for the humanities. The Guide offers concise, expert introductions to key topics, including annotated links to important standards, articles, projects, and other resources.

The best place to start is the Table of Contents grid. To find out more about the project, visit the About This Site page. Please browse, read, and contribute. We’re still expanding the site, but take a look around. Happy browsing!

— The Editors

Follow @DHCuration

More about the DH Curation Guide

Data curation is an emerging problem for the humanities as both data and analytical practices become increasingly digital. Research groups working with cultural content as well as libraries, museums, archives, and other institutions are all in need of new expertise. This Guide is a first step to understanding the essentials of data curation for the humanities. The expert-written introductions to key topics include links to important standards, documentation, articles, and projects in the field, annotated with enough context from expert editors and the research community to indicate to newcomers how these resources might help them with data curation challenges.

A Community Resource

Intended to help students and those new to the field, the DH Curation Guide also provides a quick reference for teachers, administrators, and anyone seeking an orientation in the issues and practicalities of data curation.

As indicated by the name, this community resource guide is intended to be a living, participatory document. Readers are encouraged to review and comment on every part of this guide, to suggest additional resources, and to contribute to stub articles. Contributions from readers are incorporated at intervals to keep the Guide at the cutting edge. Read more about how to contribute

Browse, comment, contribute! The table of contents provides a road map to the Guide’s current topics and those to be added soon. Read more about this site

• Maths Notes Class 9
• NCERT Solutions Class 9
• RD Sharma Solutions Class 9
• Maths Formulas Class 9
• Class 9 Syllabus
• Class 9 Revision Notes
• Physics Notes Class 9
• Chemistry Notes Class 9
• Biology Notes Class 9
• History Notes class 9
• Geography Notes class 9
• Social science Notes class 9

Graphical Representation of Data

Graphical Representation of Data: Graphical Representation of Data,” where numbers and facts become lively pictures and colorful diagrams . Instead of staring at boring lists of numbers, we use fun charts, cool graphs, and interesting visuals to understand information better. In this exciting concept of data visualization, we’ll learn about different kinds of graphs, charts, and pictures that help us see patterns and stories hidden in data.

There is an entire branch in mathematics dedicated to dealing with collecting, analyzing, interpreting, and presenting numerical data in visual form in such a way that it becomes easy to understand and the data becomes easy to compare as well, the branch is known as Statistics .

The branch is widely spread and has a plethora of real-life applications such as Business Analytics, demography, Astro statistics, and so on . In this article, we have provided everything about the graphical representation of data, including its types, rules, advantages, etc.

Table of Content

What is Graphical Representation

Types of graphical representations, line graphs, histograms , stem and leaf plot , box and whisker plot .

• Graphical Representations used in Maths

Value-Based or Time Series Graphs 

Frequency based, principles of graphical representations, advantages and disadvantages of using graphical system, general rules for graphical representation of data, frequency polygon, solved examples on graphical representation of data.

Graphics Representation is a way of representing any data in picturized form . It helps a reader to understand the large set of data very easily as it gives us various data patterns in visualized form.

There are two ways of representing data,

• Pictorial Representation through graphs.

They say, “A picture is worth a thousand words”.  It’s always better to represent data in a graphical format. Even in Practical Evidence and Surveys, scientists have found that the restoration and understanding of any information is better when it is available in the form of visuals as Human beings process data better in visual form than any other form.

Does it increase the ability 2 times or 3 times? The answer is it increases the Power of understanding 60,000 times for a normal Human being, the fact is amusing and true at the same time.

Check: Graph and its representations

Comparison between different items is best shown with graphs, it becomes easier to compare the crux of the data about different items. Let’s look at all the different types of graphical representations briefly: 

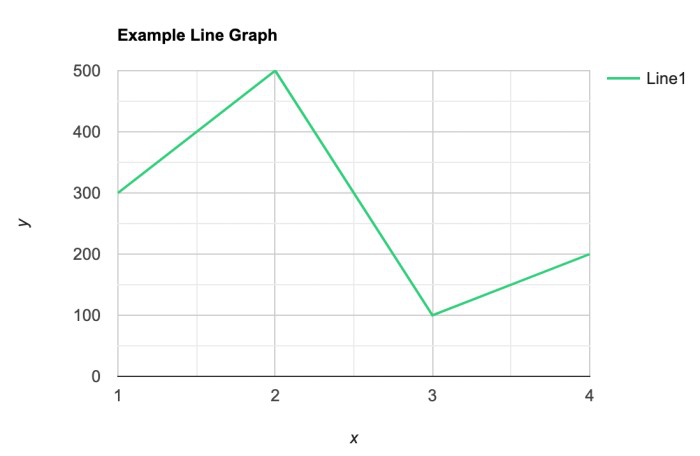
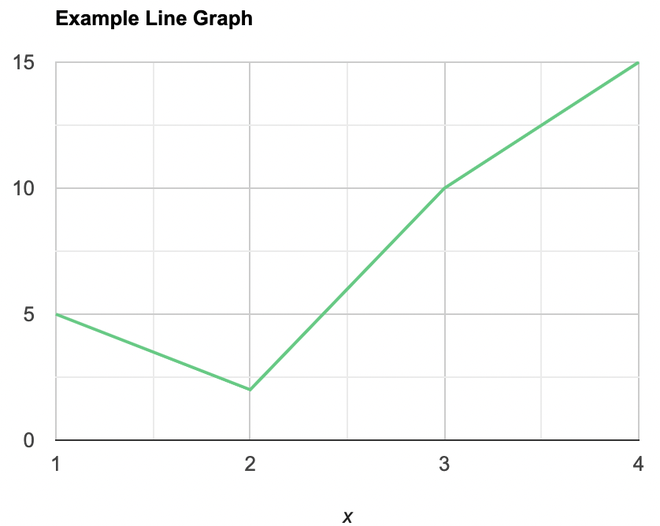
A line graph is used to show how the value of a particular variable changes with time. We plot this graph by connecting the points at different values of the variable. It can be useful for analyzing the trends in the data and predicting further trends. 

A bar graph is a type of graphical representation of the data in which bars of uniform width are drawn with equal spacing between them on one axis (x-axis usually), depicting the variable. The values of the variables are represented by the height of the bars. 

This is similar to bar graphs, but it is based frequency of numerical values rather than their actual values. The data is organized into intervals and the bars represent the frequency of the values in that range. That is, it counts how many values of the data lie in a particular range. 

It is a plot that displays data as points and checkmarks above a number line, showing the frequency of the point.  

This is a type of plot in which each value is split into a “leaf”(in most cases, it is the last digit) and “stem”(the other remaining digits). For example: the number 42 is split into leaf (2) and stem (4).  

These plots divide the data into four parts to show their summary. They are more concerned about the spread, average, and median of the data. 

It is a type of graph which represents the data in form of a circular graph. The circle is divided such that each portion represents a proportion of the whole. 

Graphical Representations used in Math’s

Graphs in Math are used to study the relationships between two or more variables that are changing. Statistical data can be summarized in a better way using graphs. There are basically two lines of thoughts of making graphs in maths: 

• Value-Based or Time Series Graphs

These graphs allow us to study the change of a variable with respect to another variable within a given interval of time. The variables can be anything. Time Series graphs study the change of variable with time. They study the trends, periodic behavior, and patterns in the series. We are more concerned with the values of the variables here rather than the frequency of those values. 

Example: Line Graph

These kinds of graphs are more concerned with the distribution of data. How many values lie between a particular range of the variables, and which range has the maximum frequency of the values. They are used to judge a spread and average and sometimes median of a variable under study.

Also read: Types of Statistical Data

• All types of graphical representations follow algebraic principles.
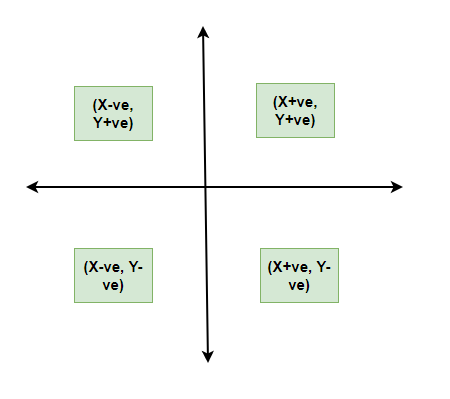
• When plotting a graph, there’s an origin and two axes.
• The x-axis is horizontal, and the y-axis is vertical.
• The axes divide the plane into four quadrants.
• The origin is where the axes intersect.
• Positive x-values are to the right of the origin; negative x-values are to the left.
• Positive y-values are above the x-axis; negative y-values are below.

• It gives us a summary of the data which is easier to look at and analyze.
• It saves time.
• We can compare and study more than one variable at a time.

Disadvantages

• It usually takes only one aspect of the data and ignores the other. For example, A bar graph does not represent the mean, median, and other statistics of the data. 
• Interpretation of graphs can vary based on individual perspectives, leading to subjective conclusions.
• Poorly constructed or misleading visuals can distort data interpretation and lead to incorrect conclusions.

Check : Diagrammatic and Graphic Presentation of Data

We should keep in mind some things while plotting and designing these graphs. The goal should be a better and clear picture of the data. Following things should be kept in mind while plotting the above graphs: 

• Whenever possible, the data source must be mentioned for the viewer.
• Always choose the proper colors and font sizes. They should be chosen to keep in mind that the graphs should look neat.
• The measurement Unit should be mentioned in the top right corner of the graph.
• The proper scale should be chosen while making the graph, it should be chosen such that the graph looks accurate.
• Last but not the least, a suitable title should be chosen.

A frequency polygon is a graph that is constructed by joining the midpoint of the intervals. The height of the interval or the bin represents the frequency of the values that lie in that interval. 

Question 1: What are different types of frequency-based plots? 

Types of frequency-based plots:  Histogram Frequency Polygon Box Plots

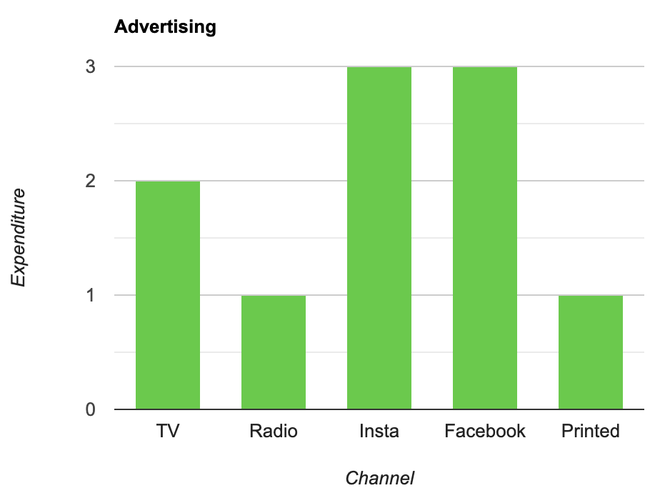
Question 2: A company with an advertising budget of Rs 10,00,00,000 has planned the following expenditure in the different advertising channels such as TV Advertisement, Radio, Facebook, Instagram, and Printed media. The table represents the money spent on different channels. 

Draw a bar graph for the following data. 

• Put each of the channels on the x-axis
• The height of the bars is decided by the value of each channel.

Question 3: Draw a line plot for the following data 

• Put each of the x-axis row value on the x-axis
• joint the value corresponding to the each value of the x-axis.

Question 4: Make a frequency plot of the following data: 

• Draw the class intervals on the x-axis and frequencies on the y-axis.
• Calculate the midpoint of each class interval.

Now join the mid points of the intervals and their corresponding frequencies on the graph. 

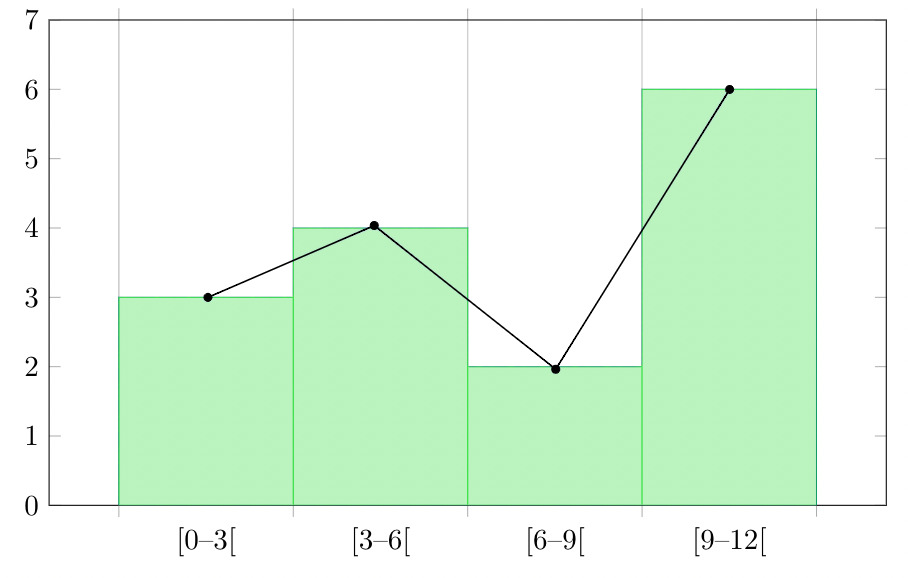
This graph shows both the histogram and frequency polygon for the given distribution.

Related Article:

Graphical Representation of Data| Practical Work in Geography Class 12 What are the different ways of Data Representation What are the different ways of Data Representation? Charts and Graphs for Data Visualization

Conclusion of Graphical Representation

Graphical representation is a powerful tool for understanding data, but it’s essential to be aware of its limitations. While graphs and charts can make information easier to grasp, they can also be subjective, complex, and potentially misleading . By using graphical representations wisely and critically, we can extract valuable insights from data, empowering us to make informed decisions with confidence.

Graphical Representation of Data – FAQs

What are the advantages of using graphs to represent data.

Graphs offer visualization, clarity, and easy comparison of data, aiding in outlier identification and predictive analysis.

What are the common types of graphs used for data representation?

Common graph types include bar, line, pie, histogram, and scatter plots , each suited for different data representations and analysis purposes.

How do you choose the most appropriate type of graph for your data?

Select a graph type based on data type, analysis objective, and audience familiarity to effectively convey information and insights.

How do you create effective labels and titles for graphs?

Use descriptive titles, clear axis labels with units, and legends to ensure the graph communicates information clearly and concisely.

How do you interpret graphs to extract meaningful insights from data?

Interpret graphs by examining trends, identifying outliers, comparing data across categories, and considering the broader context to draw meaningful insights and conclusions.

Similar Reads

• CBSE Class 9 Maths Revision Notes CBSE Class 9th Maths Revision Notes is an important phase of student’s life when they’re at a turning point in their life. The reason being class 9 is the foundation level to succeed in class 10. As you know, students must complete Class 9 in order to sit for Class 10 board examinations. Also, it la 15+ min read

Chapter 1: Number System

• Number System in Maths Number System is a method of representing numbers on the number line with the help of a set of Symbols and rules. These symbols range from 0-9 and are termed as digits. Let's learn about the number system in detail, including its types, and conversion. Number System in MathsNumber system in Maths is 13 min read
• Natural Numbers | Definition, Examples & Properties Natural numbers are the numbers that start from 1 and end at infinity. In other words, natural numbers are counting numbers and they do not include 0 or any negative or fractional numbers. For example, 3, 6, 57, 973, 4000, and so on. Natural numbers are the counting numbers: 1, 2, 3, 4, 5, and so on 11 min read
• Whole Numbers - Definition, Properties and Examples Whole numbers are a foundational concept in mathematics, encompassing all non-negative integers starting from zero. This set includes numbers like 0, 1, 2, 3, and so on, up to infinity. Unlike integers, whole numbers do not include negative numbers or fractions. Examples of Whole Numbers are 0, 2, 3 9 min read
• Prime Numbers Prime numbers are those natural numbers divisible by only 1 and the number itself. Numbers with more than two factors are called composite numbers. All primes are odd numbers except for 2. A total of 25 prime numbers are there between 1 and 100. These are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 12 min read
• Rational Numbers Rational numbers are a fundamental concept in mathematics, defined as numbers that can be expressed as the ratio of two integers, where the denominator is not zero. Represented in the form p/q​ (with p and q being integers), rational numbers include fractions, whole numbers, and terminating or repea 15+ min read
• Irrational Numbers- Definition, Examples, Symbol, Properties Irrational numbers are real numbers that cannot be expressed as fractions. Irrational Numbers can not be expressed in the form of p/q, where p and q are integers and q ≠ 0. They are non-recurring, non-terminating, and non-repeating decimals. Irrational numbers are real numbers but are different from 12 min read
• Real Numbers Real Numbers are continuous quantities that can represent a distance along a line, as Real numbers include both rational and irrational numbers. Rational numbers occupy the points at some finite distance and irrational numbers fill the gap between them, making them together to complete the real line 10 min read
• Decimal Expansion of Real Numbers The combination of a set of rational and irrational numbers is called real numbers. All the real numbers can be expressed on the number line. The numbers other than real numbers that cannot be represented on the number line are called imaginary numbers (unreal numbers). They are used to represent co 6 min read
• Decimal Expansions of Rational Numbers Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. So in this article let's discuss some rational and irrational numbers an 6 min read
• Representation of Rational Numbers on the Number Line | Class 8 Maths Rational numbers are the integers p and q expressed in the form of p/q where q>0. Rational numbers can be positive, negative or even zero. Rational numbers can be depicted on the number line. The centre of the number line is called Origin (O). Positive rational numbers are illustrated on the righ 5 min read
• Operations on Real Numbers Real Numbers are those numbers that are a combination of rational numbers and irrational numbers in the number system of maths. Real Number Operations include all the arithmetic operations like addition, subtraction, multiplication, etc. that can be performed on these numbers. Besides, imaginary num 9 min read
• Rationalization of Denominators Rationalization of Denomintors is a method where we change the fraction with an irrational denominator into a fraction with a rational denominator. If there is an irrational or radical in the denominator the definition of rational number ceases to exist as we can't divide anything into irrational pa 8 min read
• Nth Root Nth root of unity is the root of unity when taken which on taking to the power n gives the value 1. Nth root of any number is defined as the number that takes to the power of n results in the original number. For example, if we take the nth root of any number, say b, the result is a, and then a is r 7 min read
• Laws of Exponents for Real Numbers Laws of Exponents are fundamental rules used in mathematics to simplify expressions involving exponents. These laws help in solving arithmetic problems efficiently by defining operations like multiplication, division, and more on exponents. In this article, we will discuss the laws of exponent for r 6 min read

Chapter 2: Polynomials

• Polynomials in One Variable | Polynomials Class 9 Maths Polynomials in One Variable: Polynomial word originated from two words “poly” which means “many” and the word “nominal” which means “term”. In maths, a polynomial expression consists of variables known as indeterminate and coefficients. Polynomials are expressions with one or more terms with a non-z 7 min read
• Polynomial Formula Polynomial Formula gives the standard form of polynomial expressions. It specifies the arrangement of algebraic expressions according to their increasing or decreasing power of variables. Let's learn about various polynomial formulas and identities in detail. Table of Content What is Polynomial?Type 6 min read
• Types of Polynomials (Based on Terms and Degrees) Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n 9 min read
• Zeros of Polynomial Zeros of a Polynomial are those real, imaginary, or complex values when put in the polynomial instead of a variable, the result becomes zero (as the name suggests zero as well). Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing situation 14 min read
• Factorization of Polynomial Factorization is the process in which we can find factors of either a given number or the algebraic expression using various techniques such as prime factorization, factorization using algebraic identities, and factorization of a quadratic polynomial using the middle term splitting method. Factoriza 12 min read
• Remainder Theorem The Remainder Theorem is a simple yet powerful tool in algebra that helps you quickly find the remainder when dividing a polynomial by a linear polynomial, such as (x - a). Instead of performing long or synthetic division, you can use this theorem to substitute the polynomial and get the remainder d 9 min read
• Factor Theorem Factor theorem is used for finding the roots of the given polynomial. This theorem is very helpful in finding the factors of the polynomial equation without actually solving them. According to the factor theorem, for any polynomial f(x) of degree n ≥ 1 a linear polynomial (x - a) is the factor of th 11 min read
• Algebraic Identities Algebraic Identities are fundamental equations in algebra where the left-hand side of the equation is always equal to the right-hand side, regardless of the values of the variables involved. These identities play a crucial role in simplifying algebraic computations and are essential for solving vari 14 min read

Chapter 3: Coordinate Geometry

• Coordinate Geometry Coordinate geometry is the branch of mathematics that deals with plotting the curve on the coordinate axes. Various curves can be plotted on the coordinate plane using coordinate geometry formulas. Co-ordinate geometry uses algebraic equations to plot various curves on the coordinate plane. One of t 11 min read
• Cartesian Coordinate System Cartesian Coordinate System in Maths is a division of coordinate geometry where the location of a point in a plane or space is marked by a pair of numbers or three numbers. The branch of geometry that deals with the Cartesian Coordinate System is called Coordinate Geometry. The numbers which are use 15+ min read
• Cartesian Plane Cartesian plane is defined as the two-dimensional plane used in the Cartesian coordinate system. This plane is formed by intersecting two perpendicular lines called the x-axis and the y-axis and their intersection is called the origin. This method of distributing the 2-Dimensional space into four ar 9 min read

Chapter 4: Linear equations in two variables

• Linear Equations in One Variable Linear equation in one variable is the equation that is used in algebra for finding unknown quantities. It is used for representing the conditions that are dependent on one variable. It is a linear equation i.e. the equation in which the degree of the equation is one, and it only has one variable. L 8 min read
• Linear Equation in Two Variables Linear Equation in Two Variables: A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variables comes into the picture, it means that the entire equation has 2 variables presen 9 min read
• Graph of Linear Equations in Two Variables Linear equations are the first-order equations, i.e. the equations of degree 1. The equations which are used to define any straight line are linear, they are represented as,  x + k = 0;  These equations have a unique solution and can be represented on number lines very easily. Let's look at linear e 5 min read
• Graphical Methods of Solving Pair of Linear Equations in Two Variables A system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr 8 min read

Chapter 5: Introduction to Euclid's Geometry

• Euclidean Geometry Euclidean geometry is the study of 2-Dimensional geometrical shapes and figures. Euclidean geometry is based on different axioms and theorems. The word geometry is derived from the Greek words ‘geo’ meaning Earth and ‘metrein’ meaning ‘To measure’. Thus, geometry is the measure of the Earth or vario 15 min read
• Equivalent Version of Euclid’s Fifth Postulate Geometry has originated from a variety of civilizations. Almost every major civilization has studied and used geometry in its prime. Egyptian and Indian civilizations were more focused on using geometry as a tool. Euclid came and changed the way people used to think in geometry. Instead of making it 6 min read

Chapter 6: Lines and Angles

• Lines and Angles Lines and Angles are the basic terms used in the Geometry. They provide a base for understanding all the concepts of geometry. We define a line as a 1-D figure which can be extended to infinity in opposite directions, whereas an angle is defined as the opening created by joining two or more lines. A 10 min read
• Types of Angles Types of Angles: An angle is a geometric figure formed by two rays meeting at a common endpoint. It is measured in degrees or radians. It deals with the relationship of points, lines, angles, and shapes in space. Understanding different types of angles is crucial for solving theoretical problems in 10 min read
• Pairs of Angles - Lines & Angles When two lines share a common endpoint, called Vertex then an angle is formed between these two lines and when these angles appear in groups of two to display a specific geometrical property then they are called pairs of angles. Understanding these angle pairs helps in solving geometry problems invo 8 min read
• Transversal Lines Transversal Lines in geometry is defined as a line that intersects two lines at distinct points in a plane. The transversal line intersecting a pair of parallel lines is responsible for the formation of various types of angles that, include alternate interior angles, corresponding angles, and others 7 min read
• Angle Sum Property of a Triangle Angle Sum Property of a Triangle is the special property of a triangle that is used to find the value of an unknown angle in the triangle. It is the most widely used property of a triangle and according to this property, "Sum of All the Angles of a Triangle is equal to 180º." Angle Sum Property of a 8 min read

Chapter 7: Triangles

• Triangles in Geometry Triangles in Geometry: A Triangle is a polygon with three sides and three corners. The corners are also known as vertices, and the sides that connect them are called edges. The interior of a triangle is a two-dimensional region. A triangle is the simplest form of a Polygon. Triangles can be classifi 15+ min read
• Congruence of Triangles |SSS, SAS, ASA, and RHS Rules Congruence of triangles is a concept in geometry which is used to compare different shapes. It is the condition between two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each othe 10 min read
• Theorem - Angle opposite to equal sides of an isosceles triangle are equal | Class 9 Maths In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Exampl 4 min read
• Triangle Inequality Theorem, Proof & Applications Triangle Inequality Theorem is the relation between the sides and angles of triangles which helps us understand the properties and solutions related to triangles. Triangles are the most fundamental geometric shape as we can't make any closed shape with two or one side. Triangles consist of three sid 9 min read

Chapter 8: Quadrilateral

• Angle Sum Property of a Quadrilateral Angle Sum Property of a Quadrilateral: Quadrilaterals are encountered everywhere in life, every square rectangle, any shape with four sides is a quadrilateral. We know, three non-collinear points make a triangle. Similarly, four non-collinear points take up a shape that is called a quadrilateral. It 9 min read
• Quadrilaterals Quadrilateral is a two-dimensional figure characterized by having four sides, four vertices, and four angles. It can be broadly classified into two categories: concave and convex. Within the convex category, there are several specific types of quadrilaterals, including trapezoids, parallelograms, re 12 min read
• Introduction to Parallelogram | Properties, Types, and Theorem A parallelogram is a two-dimensional geometrical shape whose opposite sides are equal in length and parallel. The opposite angles of a parallelogram are equal in measure and the Sum of adjacent angles of a parallelogram is equal to 180 degrees. In this article, we will learn about the definition of 12 min read
• Rhombus: Definition, Properties, Formula and Examples Rhombus is a quadrilateral with all four sides equal and opposite sides parallel to each other. The opposite angles of a rhombus are equal. Any rhombus can be considered a parallelogram, but not all parallelograms are rhombus. A rhombus is a unique type of quadrilateral known for its equal-length si 9 min read
• Trapezium in Maths | Formulas, Properties & Examples Trapezium in Maths: A Trapezium is a polygon with four sides, i.e. it is a quadrilateral. Trapezium originated from the Greek word "trapeze" which means table. It is a complex quadrilateral. A trapezium is a special quadrilateral with only one pair of parallel sides. A trapezium is a two-dimensional 12 min read
• Square in Maths - Area, Perimeter, Examples & Applications Square is a type of quadrilateral with four sides. What distinguishes a square from other quadrilaterals is that all four sides of a square are of equal length, and all four interior angles are right angles (90 degrees). Let's learn about Square, including its properties, area, perimeter, examples, 9 min read
• Kite - Quadrilaterals A Kite is a special type of quadrilateral that is easily recognizable by its unique shape, resembling the traditional toy flown on a string. In geometry, a kite has two pairs of adjacent sides that are of equal length. This distinctive feature sets it apart from other quadrilaterals like squares, re 8 min read
• Properties of Parallelograms Properties of Parallelograms: Parallelogram is a quadrilateral in which opposite sides are parallel and congruent and the opposite angles are equal. A parallelogram is formed by the intersection of two pairs of parallel lines. In this article, we will learn about the properties of parallelograms, in 9 min read
• Mid Point Theorem The Midpoint Theorem is a fundamental concept in geometry that simplifies solving problems involving triangles. It establishes a relationship between the midpoints of two sides of a triangle and the third side. This theorem is especially useful in coordinate geometry and in proving other mathematica 6 min read

Chapter 9: Areas of Parallelograms and Triangles

• Area of Triangle | Formula and Examples Area of the triangle is a basic geometric concept that calculates the measure of the space enclosed by the three sides of the triangle. The formulas to find the area of a triangle include the base-height formula, Heron's formula, and trigonometric methods. The area of triangle is generally calculate 8 min read
• Area of Parallelogram | Definition, Formulas & Examples The area of a Parallelogram is the space or the region enclosed by the boundary of the parallelogram in a two-dimensional space. It is calculated by multiplying the base of the parallelogram by its height. In this article, we will learn more about the Area of Parallelogram Formulas, and how to use t 10 min read
• Figures on the Same Base and between the Same Parallels A triangle is a three-sided polygon and a parallelogram is a four-sided polygon or simply a quadrilateral that has parallel opposite sides. We encounter these two polynomials almost everywhere in our everyday lives. For example: Let's say a farmer has a piece of land that is in the shape of a parall 6 min read

Chapter 10: Circles

• Circles in Maths Circles in Maths: A circle is a two-dimensional shape where all points on the circumference are the same distance from the centre. In other words, it is a collection of all points in a plane that are the same distance away from a fixed point, called the centre. Its area is equal to pi times the squa 15 min read
• Radius of Circle Radius of Circle: The radius of a circle is the distance from the circle's center to any point on its circumference. It is commonly represented by 'R' or 'r'. The radius is crucial in nearly all circle-related formulas, as the area and circumference of a circle are also calculated using the radius. 8 min read
• Tangent to a Circle Tangent in Circles are the line segments that touch the given curve only at one particular point. Tangent is a Greek word meaning "To Touch". For a circle, we can say that the line which touches the circle from the outside at one single point on the circumference is called the tangent of the circle. 10 min read
• What is the longest chord of a Circle? Geometry OverviewGeometry is the major part of mathematics that deals with lines, angles, points, etc. They are the visual study of shapes and sizes. The geometric approach is seen everywhere around us as every object has a certain shape whose parameters can be studied with the help of geometrical f 5 min read
• Circumference of Circle - Definition, Perimeter Formula, and Examples The circumference of a circle is the distance around its boundary, much like the perimeter of any other shape. It is a key concept in geometry, particularly when dealing with circles in real-world applications such as measuring the distance traveled by wheels or calculating the boundary of round obj 8 min read
• Angle subtended by an arc at the centre of a circle Given the angle subtended by an arc at the circle circumference X, the task is to find the angle subtended by an arc at the centre of a circle.For eg in the below given image, you are given angle X and you have to find angle Y. Examples: Input: X = 30 Output: 60Input: X = 90 Output: 180 Approach: Wh 3 min read
• What is Cyclic Quadrilateral Cyclic Quadrilateral is a special type of quadrilateral in which all the vertices of the quadrilateral lie on the circumference of a circle. In other words, if you draw a quadrilateral and then find a circle that passes through all four vertices of that quadrilateral, then that quadrilateral is call 9 min read
• The sum of opposite angles of a cyclic quadrilateral is 180° | Class 9 Maths Theorem In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the cir 6 min read

Chapter 11: Construction

• Basic Constructions - Angle Bisector, Perpendicular Bisector, Angle of 60° Most of the time we use diagrams while depicting the shapes and scenarios in mathematics. But they are not precise, they are just a representation of the actual shape without proper measurements. But when we are building something like a wooden table, or map of a building is to be constructed. It ne 5 min read
• Construction of Triangles Triangles are three-sided polygon which have three vertices. Basic construction techniques allow us to construct triangles. An important property of the triangle is that sum of internal angles of a triangle is 180°.  SAS, SSS, ASA, and RHS are the rules of congruency of two triangles. A triangle is 8 min read

Chapter 12: Heron's Formula

• Area of Equilateral Triangle The area of an equilateral triangle is the amount of space enclosed within its three equal sides. For an equilateral triangle, where all three sides and all three internal angles are equal (each angle measuring 60 degrees), the area can be calculated using the formula [Tex]\frac{\sqrt{3}}{4}\times a 6 min read
• Area of Isosceles Triangle Area of Isosceles triangle is the space enclosed by the sides of a triangle. The general formula for finding the area of the isosceles triangle is given by half the product of the base and height of the triangle. Other than this different formulas are used to find the area of triangles. Triangles ar 10 min read
• Heron's Formula Heron's formula is a very popular formula for finding the area of a triangle when the three sides are given. This formula was given by "Heron" in his book "Metrica". We can apply this formula to all types of triangles, be they right-angled, equilateral, or isosceles. Heron's formula, attributed to H 12 min read
• Applications of Heron's Formula While solving and finding the Area of a Triangle, Certain parameters are expected to be provided beforehand, for example, the height and the base of the triangle must be available Or in the case of an Equilateral Triangle, the lengths of the side should be given. Heron's formula is basically for a t 10 min read
• Area of Quadrilateral Area of Quadrilateral: The Area of a quadrilateral is the space inside the boundary of a quadrilateral or in other words, the space enclosed by the edges of a quadrilateral. A quadrilateral is a closed two-dimensional shape with four sides or edges, and also four corners or vertices. In mensuration, 11 min read
• Area of Polygons Area of the Polygon is the area enclosed by the boundary of the polygon. A polygon is a closed, two-dimensional shape with straight sides. Each side of a polygon is a line segment, and the points where the sides meet are called vertices. A polygon is a figure formed by joining 'n' straight lines suc 15 min read

Chapter 13: Surface Areas and Volumes

• Surface Area of Cuboid The surface area of a cuboid is the total space occupied by all its surfaces/sides. In geometry, a three-dimensional shape having six rectangular faces is called a cuboid. A cuboid is also known as a regular hexahedron and has six rectangular faces, eight vertices, and twelve edges with congruent, o 12 min read
• Volume of Cuboid | Formula and Examples Volume of a cuboid is calculated using the formula V = L × B × H, where V represents the volume in cubic units, L stands for length, B for breadth, and H for height. Here, the breadth and width of a cuboid are the same things. The volume signifies the amount of space occupied by the cuboid in three 8 min read
• Surface Area of Cube | Curved & Total Surface Area Surface area of a cube is defined as the total area covered by all the faces of a cube. In geometry, the cube is a fascinating three-dimensional object that we encounter daily, from dice to ice cubes. But have you ever wondered about the total area that covers a cube? This is what we call the surfac 15 min read
• Volume of a Cube Volume of a Cube is defined as the total number of cubic units occupied by the cube completely. A cube is a three-dimensional solid figure, having 6 square faces. Volume is nothing but the total space occupied by an object. An object with a larger volume would occupy more space. The volume of the cu 9 min read
• Surface Area of Cylinder | Curved and Total Surface Area of Cylinder Surface Area of a Cylinder is the amount of space covered by the flat surface of the cylinder's bases and the curved surface of the cylinder. The total surface area of the cylinder includes the area of the cylinder's two circular bases as well as the area of the curving surface. The volume of a cyli 10 min read
• Volume of a Cylinder| Formula, Definition and Examples Volume of a cylinder is a fundamental concept in geometry and plays a crucial role in various real-life applications. It is a measure which signifies the amount of material the cylinder can carry. It is also defined as the space occupied by the Cylinder. The formula for the volume of a cylinder is π 11 min read
• Surface Area of Cone Surface Area of a Cone is the total area encompassing the circular base and the curved surface of the cone. A cone has two types of surface areas. If the radius of the base is 'r' and the slant height is 'l', we use two formulas: Total Surface Area (TSA) of the cone = πr(r + l)Curved Surface Area (C 8 min read
• Volume of Cone- Formula, Derivation and Examples Volume of a cone can be defined as the space occupied by the cone. As we know, a cone is a three-dimensional geometric shape with a circular base and a single apex (vertex). Let's learn about Volume of Cone in detail, including its Formula, Examples, and the Frustum of Cone. Volume of ConeA cone's v 10 min read
• Surface Area of Sphere | Formula, Derivation and Solved Examples A sphere is a three-dimensional object with all points on its surface equidistant from its center, giving it a perfectly round shape. The surface area of a sphere is the total area that covers its outer surface. To calculate the surface area of a sphere with radius r, we use the formula: Surface Are 8 min read
• Volume of a Sphere The volume of a sphere helps us understand how much space a perfectly round object occupies, from tiny balls to large planets. Using the simple volume of sphere formula, you can easily calculate the space inside any sphere. Whether you're curious about the volume of a solid sphere in math or science 8 min read
• Surface Area of a Hemisphere A hemisphere is a 3D shape that is half of a sphere's volume and surface area. The surface area of a hemisphere comprises both the curved region and the base area combined. Hemisphere's Total Surface Area (TSA) = Curved Surface Area + Base Area = 3πr² square units.Curved Surface Area (CSA) = 2πr² sq 13 min read
• Volume of Hemisphere Volume of a shape is defined as how much capacity a shape has or we can say how much material was required to form that shape. A hemisphere, derived from the Greek words "hemi" (meaning half) and "sphere," is simply half of a sphere. If you imagine slicing a perfectly round sphere into two equal hal 6 min read

Chapter 14: Statistics

• Collection and Presentation of Data We come across a lot of information every day from different sources. Our newspapers, TV, Phone and the Internet, etc are the sources of information in our life. This information can be related to anything, from bowling averages in cricket to profits of the company over the years. These facts and fi 10 min read
• Graphical Representation of Data Graphical Representation of Data: Graphical Representation of Data," where numbers and facts become lively pictures and colorful diagrams. Instead of staring at boring lists of numbers, we use fun charts, cool graphs, and interesting visuals to understand information better. In this exciting concept 8 min read
• Bar Graphs and Histograms Bar graphs and Histograms: The science of collecting and analyzing data in large quantities, especially for inferring proportions in a whole form is known as Statistics. The word 'statistics' itself refers to numbers that are used to describe the relationships of data. Therefore, we can say that the 8 min read
• Central Tendency in Statistics- Mean, Median, Mode Central Tendencies are the numerical values that are used to represent a large collection of numerical data. These obtained numerical values are called central or average values. A central or average value of any statistical data or series is the variable's value representative of the entire data or 9 min read
• Mean, Median and Mode Mean, Median, and Mode are measures of the central tendency. These values are used to define the various parameters of the given data set. The measure of central tendency (Mean, Median, and Mode) gives useful insights about the data studied, these are used to study any type of data such as the avera 15 min read

Chapter 15: Probability

• Experimental Probability Experimental probability, also known as empirical probability, is a concept in mathematics that deals with estimating the likelihood of an event occurring based on actual experimental results. Unlike theoretical probability, which predicts outcomes based on known possibilities, experimental probabil 8 min read
• Empirical Probability Empirical Probability: Probability describes the chance that an uncertain event will occur. Empirical probability is based on how likely an event has occurred in the past. It is also called experimental probability. It is based on the relative frequency approach. We can get our results from experien 7 min read
• CBSE Class 9 Maths Formulas GeeksforGeeks present Maths Chapterwise Formulas for Class 9. This is designed for the convenience of the students so that one can understand all the important concepts of Class 9 Mathematics directly and easily. Math formulae for Class 9 are offered here for students who find the topic of mathemati 15+ min read
• NCERT Solutions for Class 9 Maths 2024-25: Chapter Wise PDF Download NCERT Solutions for Class 9 Maths offers complete answers to all questions in the NCERT textbook, covering topics like Number Systems, Coordinate Geometry, Polynomials, Euclid's Geometry, Quadrilaterals, Triangles, Circles, Constructions, Surface Areas, Volumes, Statistics, and Probability. If you a 15+ min read
• RD Sharma Class 9 Solutions RD Sharma Solutions for class 9 provides vast knowledge about the concepts through the chapter-wise solutions. These solutions help to solve problems of higher difficulty and to ensure students have a good practice of all types of questions that can be framed in the examination. Referring to the sol 10 min read
• Mathematics
• School Learning
• Maths-Class-9

Improve your Coding Skills with Practice

What kind of Experience do you want to share?