research mean median mode

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Measures of central tendency: Median and mode

S manikandan.

• Author information
• Copyright and License information

Address for correspondence: Manikandan S Indira Gandhi Medical College and Research Institute Hospital, Pondicherry, India E-mail: [email protected]

This is an open-access article distributed under the terms of the Creative Commons Attribution-Noncommercial-Share Alike 3.0 Unported, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

INTRODUCTION

Apart from the mean, median and mode are the two commonly used measures of central tendency. The median is sometimes referred to as a measure of location as it tells us where the data are.[ 1 ] This article describes about median, mode, and also the guidelines for selecting the appropriate measure of central tendency.

Median is the value which occupies the middle position when all the observations are arranged in an ascending/descending order. It divides the frequency distribution exactly into two halves. Fifty percent of observations in a distribution have scores at or below the median. Hence median is the 50th percentile.[ 2 ] Median is also known as ‘positional average’.[ 3 ]

It is easy to calculate the median. If the number of observations are odd, then ( n + 1)/2th observation (in the ordered set) is the median. When the total number of observations are even, it is given by the mean of n /2th and ( n /2 + 1)th observation.[ 2 ]

It is easy to compute and comprehend.

It is not distorted by outliers/skewed data.[ 4 ]

It can be determined for ratio, interval, and ordinal scale.

Disadvantages

It does not take into account the precise value of each observation and hence does not use all information available in the data.

Unlike mean, median is not amenable to further mathematical calculation and hence is not used in many statistical tests.

If we pool the observations of two groups, median of the pooled group cannot be expressed in terms of the individual medians of the pooled groups.

Mode is defined as the value that occurs most frequently in the data. Some data sets do not have a mode because each value occurs only once. On the other hand, some data sets can have more than one mode. This happens when the data set has two or more values of equal frequency which is greater than that of any other value. Mode is rarely used as a summary statistic except to describe a bimodal distribution. In a bimodal distribution, the taller peak is called the major mode and the shorter one is the minor mode.

It is the only measure of central tendency that can be used for data measured in a nominal scale.[ 5 ]

It can be calculated easily.

It is not used in statistical analysis as it is not algebraically defined and the fluctuation in the frequency of observation is more when the sample size is small.

POSITION OF MEASURES OF CENTRAL TENDENCY

The relative position of the three measures of central tendency (mean, median, and mode) depends on the shape of the distribution. All three measures are identical in a normal distribution [ Figure 1a ]. As mean is always pulled toward the extreme observations, the mean is shifted to the tail in a skewed distribution [Figure 1b and c ]. Mode is the most frequently occurring score and hence it lies in the hump of the skewed distribution. Median lies in between the mean and the mode in a skewed distribution.[ 6 , 7 ]

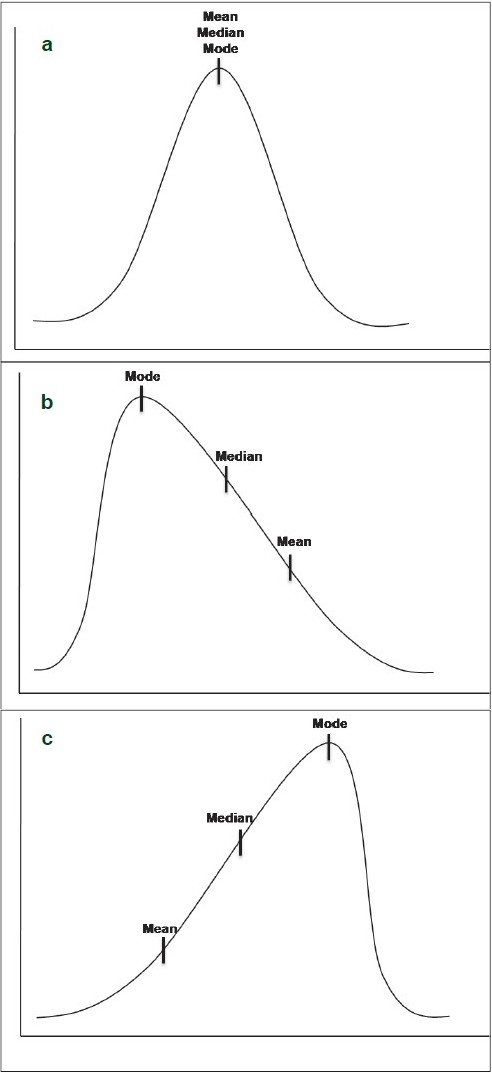
The relative position of the various measures of central tendency. (a) Normal distribution (b) Positively (right) skewed distribution (c) Negatively (left) skewed distribution

SELECTING THE APPROPRIATE MEASURE

Mean is generally considered the best measure of central tendency and the most frequently used one. However, there are some situations where the other measures of central tendency are preferred.

Median is preferred to mean[ 3 ] when

There are few extreme scores in the distribution.

Some scores have undetermined values.

There is an open ended distribution.

Data are measured in an ordinal scale.

Mode is the preferred measure when data are measured in a nominal scale. Geometric mean is the preferred measure of central tendency when data are measured in a logarithmic scale.[ 8 ]

Source of Support: Nil

Conflict of Interest: None declared.

• 1. Swinscow TD, Campbell MJ. 10th ed(Indian) New Delhi: Viva Books Private Limited; 2003. Statistics at square one. [ Google Scholar ]
• 2. Gravetter FJ, Wallnau LB. 5th ed. Belmont: Wadsworth – Thomson Learning; 2000. Statistics for the behavioral sciences. [ Google Scholar ]
• 3. Sundaram KR, Dwivedi SN, Sreenivas V. 1st ed. New Delhi: B.I Publications Pvt Ltd; 2010. Medical statistics principles and methods. [ Google Scholar ]
• 4. Petrie A, Sabin C. 3rd ed. Oxford: Wiley-Blackwell; 2009. Medical statistics at a glance. [ Google Scholar ]
• 5. Norman GR, Streiner DL. 2nd ed. Hamilton: B.C. Decker Inc; 2000. Biostatistics the bare essentials. [ Google Scholar ]
• 6. SundarRao PS, Richard J. 4th ed. New Delhi: Prentice Hall of India Pvt Ltd; 2006. Introduction to biostatistics and research methods. [ Google Scholar ]
• 7. Glaser AN. 1st Indian Ed. New Delhi: Lippincott Williams and Wilkins; 2000. High Yield Biostatistics. [ Google Scholar ]
• 8. Dawson B, Trapp RG. 4th ed. New York: Mc-Graw Hill; 2004. Basic and Clinical Biostatistics. [ Google Scholar ]
• View on publisher site
• PDF (390.5 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Mean, Mode and Median

Mean, mode and median are popular quantitative research methods used in business, as well as, engineering and computer sciences. In business studies these methods can be used in data comparisons such as comparing performances of two different businesses within the same period of time or comparing performance of the same business during different time periods.

Mean implies average and it is the sum of a set of data divided by the number of data. Mean can prove to be an effective tool when comparing different sets of data; however this method might be disadvantaged by the impact of extreme values.

Mode is the value that appears the most. A given set of data can contain more than one mode, or it can contain no mode at all. Extreme values have no impact on mode in data comparisons, however, the effectiveness of mode in data comparisons are compromised in the presence of more than one mode.

Median is the middle value when the data is arranged in numerical order. It is another effective tool to compare different sets of data, however, the negative impact of extreme values is lesser on median compared to mean.

John Dudovskiy

LEARN STATISTICS EASILY

Learn Data Analysis Now!

Measures of Central Tendency: Mean, Mode, Median

You will learn the distinct applications and nuances of the central tendency measures mean, mode, median in data analysis.

Introduction

In statistics, the concept of central tendency is pivotal. It encompasses identifying a single value that best represents a data set. This value is critical in understanding a dataset’s overall trend or center. The measures of central tendency — mean, mode, and median — each offers unique perspectives on the data, enabling statisticians and data analysts to derive meaningful insights.

Understanding and applying these measures correctly is fundamental in statistical analysis. They are foundational tools for summarizing and interpreting data, essential in various fields, including economics, psychology, biology, and more. These measures help make informed decisions based on data and understand the general behavior or characteristics of the data set. For a comprehensive analysis, it is crucial to calculate these measures and comprehend their implications in the context of the data’s distribution and characteristics.

• The mean is sensitive to outliers, impacting its representativeness in skewed distributions.
• Median provides a better central value in skewed data unaffected by extreme values.
• Mode is critical in understanding the most frequent occurrence in categorical data.
• Comparing these measures can unveil data distribution characteristics.
• Skewed distributions often require median over mean for an accurate central tendency.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

The mean, often called the average, is a fundamental concept in statistics and data analysis . It is calculated by summing all values in a dataset and dividing this total by the number of values. Mathematically, it’s expressed as:

Mean= n ∑ i =1 n ​ xi ​​

where  xi ​ represents each value in the dataset, and  n  is the number of values.

Applications and Limitations of the Mean

The mean is widely used due to its simplicity and straightforward interpretation. It’s beneficial when the data is normally distributed, as it provides a central location for the data. In fields like economics, psychology, and biology, the mean is used to analyze everything from test scores and temperatures to biological measurements.

However, the mean has its limitations. One of its most significant drawbacks is its sensitivity to outliers — extreme values significantly different from the rest of the data. In skewed distributions, outliers can drastically alter the mean, making it a less reliable measure of central tendency. This can mislead interpretations, especially when the data is not symmetrically distributed.

Visual Aids and Examples

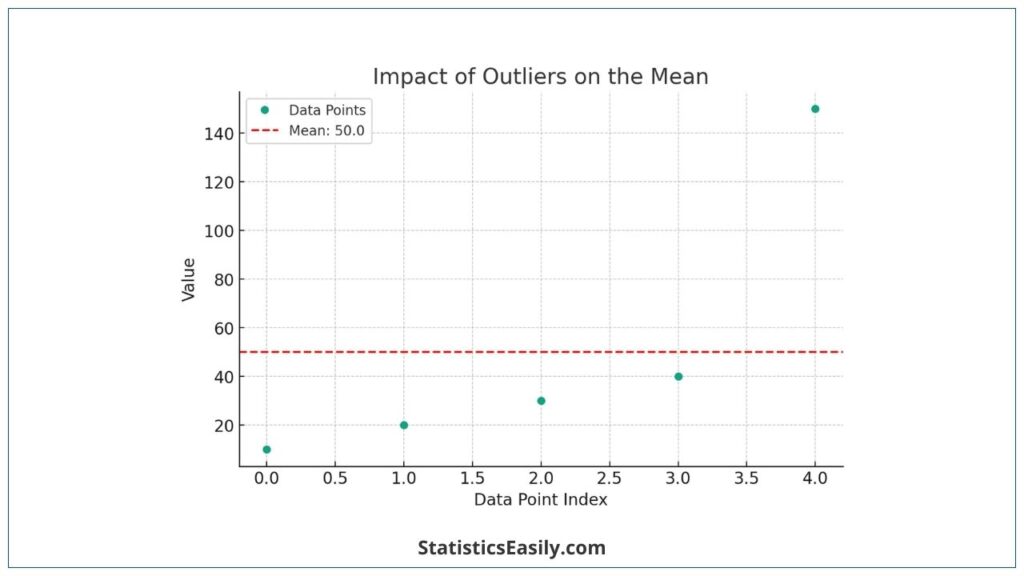
Consider a dataset: 10,20,30,40,150. The mean of this dataset is 50, calculated as (10+20+30+40+150)/5. However, notice how the value 150 (an outlier ) significantly influences the mean, making it higher than most data points in the set.

To visually represent the effect of outliers on the mean, let’s create a graph that includes this dataset, highlighting the mean and the impact of the outlier.

The median is a robust measure of central tendency, representing the middle value in a sorted dataset. It is calculated by arranging all values from the lowest to the highest and finding the central number. The median is the middle value in a dataset with an odd number of values. For even-numbered datasets, it is the average of the two middle values. Mathematically, if  n  is odd, the median is the ( n +1)/2th value. If  n  is even, it is the average of the 2 n /2th and ( n /2)+1th values.

Applications and Use Cases of the Median

The median is particularly useful in skewed distributions or datasets with outliers. Unlike the mean, it is not affected by extremely high or low values, making it a more representative measure of central tendency in such cases. This characteristic makes the median highly applicable in fields like real estate, income analysis, and any scenario where outliers are common and can skew the data.

Examples and Visual Aids

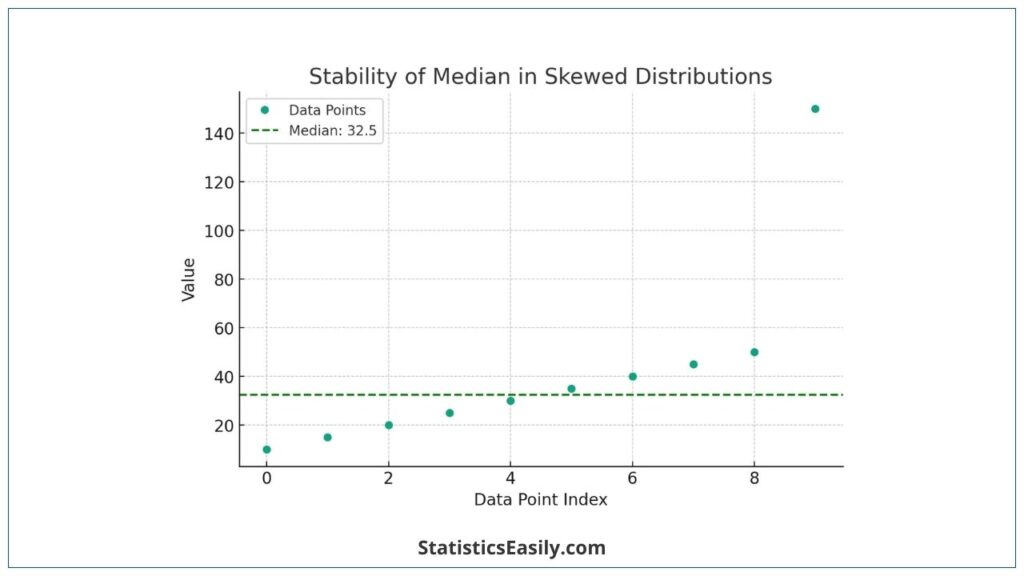
Consider a dataset: 10,20,30,40,150. The median of this dataset is 30, which is the middle value when the data is sorted. The high value 150 does not affect the median as it does the mean.

To illustrate the median’s utility in skewed distributions, let’s create a graph representing this concept with a dataset that includes outliers. This visual representation will demonstrate how the median remains stable even in extreme values.

The mode is the value that appears most frequently in a dataset. Unlike mean and median, the mode is not necessarily unique, leading to datasets that can be unimodal (one mode), bimodal (two modes), or multimodal (more than two modes). Calculating the mode involves identifying the frequency of each value in the dataset and determining which value(s) occur most often.

Applications and Limitations of the Mode

The mode is handy in analyzing categorical data where numerical averages may not be meaningful, such as determining the most preferred brand in a consumer survey. It is also valuable in identifying trends or commonalities within datasets, such as the most common symptoms in a medical study or the most occurring sales item in a store.

However, the mode’s utility is limited by its dependence on the frequency of values. The mode may not be informative in datasets where values are uniformly distributed or where each value occurs with a similar frequency. Additionally, in continuous numerical data, the concept of mode becomes less clear since the probability of two values being the same is low.

Consider a dataset: 10,20,20,30,40. The mode of this dataset is 20, as it appears more frequently than any other value.

To illustrate the concept of mode, let’s create a graph representing a dataset with a modal distribution. This will help visualize how the mode can indicate the most common values in a dataset.

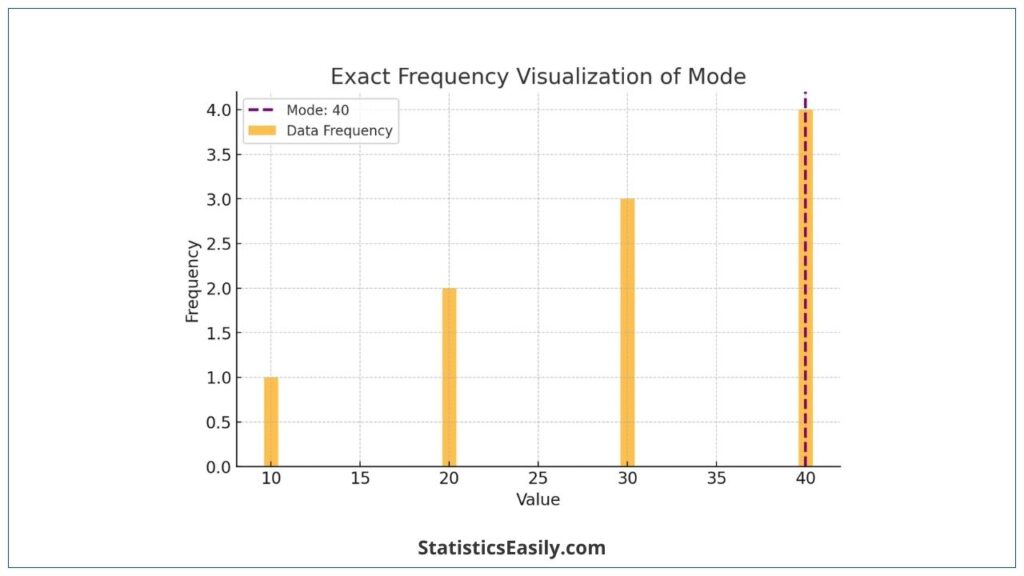
Comparative Analysis

Understanding the differences and appropriate applications of mean, median, and mode is crucial in statistical analysis. Each measure of central tendency has unique characteristics that make it suitable for specific scenarios. Let’s compare these measures using various datasets to highlight their differences and use cases.

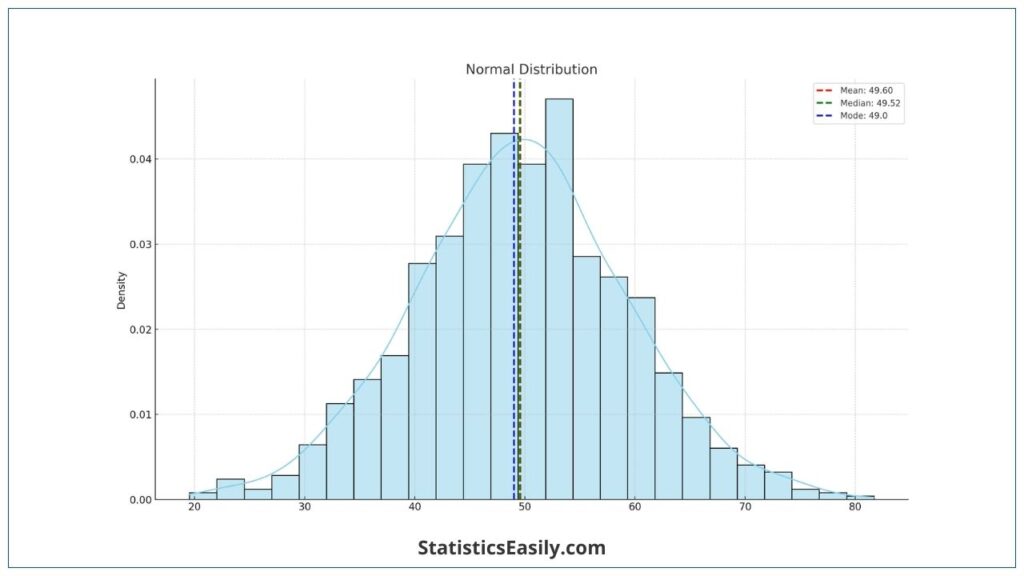
Normal Distribution:

• Mean:  Effectively represents the central tendency as data is symmetrically distributed.
• Median:  Aligns closely with the mean in a normal distribution.
• Mode:  Typically coincides with the mean and median in a perfectly normal distribution.

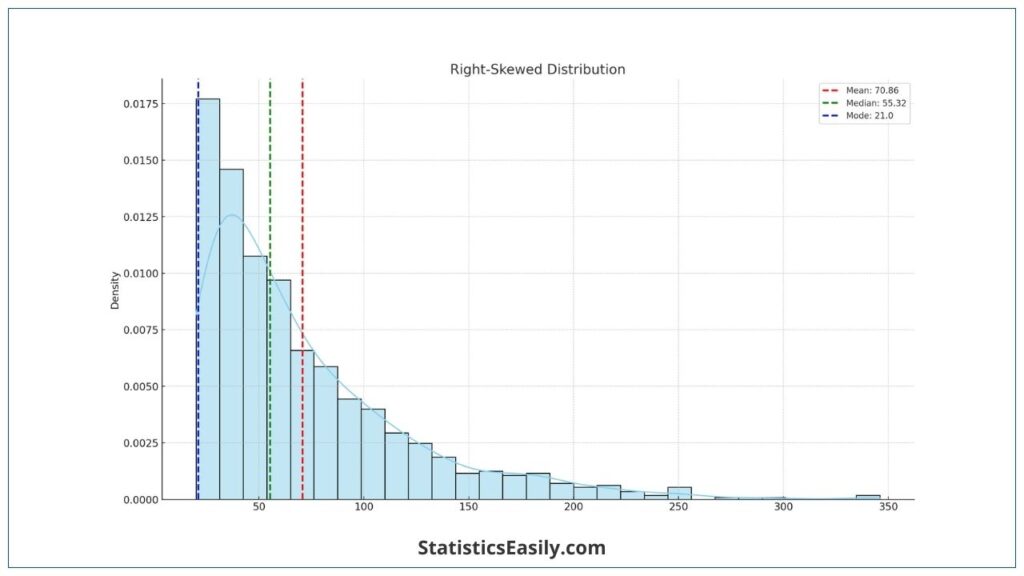
Skewed Distribution (Right-Skewed):

• Mean:  Higher than median and mode due to the influence of outliers on the right.
• Median:  More representative of the dataset’s central tendency than the mean.
• Mode:  Least affected by outliers, indicating the most frequent value.

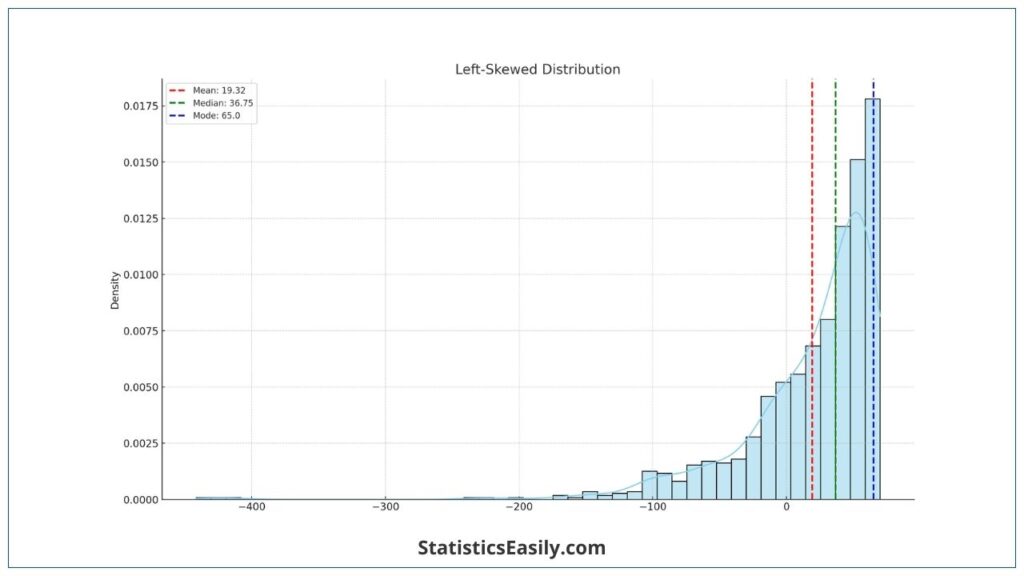
Skewed Distribution (Left-Skewed):

• Mean:  Lower than both median and mode, influenced by low-value outliers.
• Median:  Provides a better central value than the mean.
• Mode:  Represents the most common value in the dataset.

Bimodal Distribution:

• Mean:  Provides an average that may not represent any typical value.
• Median:  Offers a middle value but may not indicate the frequency of occurrence.
• Mode:  Highlights the two most frequent values, helpful in identifying multiple peaks.

Let’s create a table summarizing these scenarios and representative graphs for each distribution for visual comparison.

Advanced Considerations

Skewed Distributions:

Skewed distributions occur when data points are not symmetrically distributed around the mean, resulting in a dataset that is either right-skewed (positively skewed) or left-skewed (negatively skewed). In such distributions, the mean is pulled towards the tail and is no longer a reliable central point.

Right-Skewed Distribution:  The mean is often greater than the median due to the pull of high-value outliers. For example, the mean can be misleadingly higher than the median in income data, where a few individuals have significantly higher incomes.

Left-Skewed Distribution:  Conversely, the mean is less than the median in left-skewed distributions, influenced by low-value outliers. An example can be found in age distributions in specific populations where a higher concentration of younger individuals can skew the mean age downwards.

Impact of Outliers:

Outliers are data points significantly different from the rest of the data. They can drastically affect the mean, as it incorporates all data points into its calculation.

Effect on Mean:  In the presence of outliers, the mean can become an unrepresentative measure of central tendency. For instance, in a dataset of house prices, a few extremely high-priced houses can significantly increase the mean, providing an inaccurate picture of the typical house price.

Stability of Median and Mode:  The median, being the middle value, is less affected by outliers and often provides a more accurate representation of central tendency in skewed distributions. As the most frequent value, the mode remains unaffected by outliers. It can offer insights into the most common occurrence in the data.

Practical Applications

Below are real-world examples and case studies demonstrating how these measures are effectively used:

Mean in Economics and Finance:

• In economics, the mean is used to calculate the average income or expenditure of populations, which is crucial for policy-making and economic planning.
• In finance, the mean return of investment portfolios is analyzed to assess performance and make investment decisions.

Median in Real Estate and Sociology:

• The median house price is a commonly reported statistic in real estate. It provides a more accurate representation of the housing market than the mean, which can be skewed by extremely high or low values.
• Sociologists use the median to study income distribution within societies, as it gives a clearer picture of the middle-income bracket, especially in cases of income inequality.

Mode in Market Research and Retail:

• Market researchers use the mode to identify consumers’ most popular product features or preferences, guiding product development and marketing strategies.
• Retailers analyze sales data to determine the most frequently purchased items, using the mode to stock products effectively and plan promotions.

Case Study: Health and Medicine:

• In medical research, the mean blood pressure level of a population might be studied to understand overall health trends. However, in cases with outliers (extremely high or low values), the median can provide a more representative measure of central blood pressure trends.
• Epidemiologists often use the mode to identify a disease’s most common symptoms or characteristics, which can be critical in diagnosing and understanding the spread of illnesses.

Historical Data Analysis:

• Historians and researchers might use these measures to analyze trends, such as the mean income level during different historical periods or the median age of populations in various eras.

In each of these applications, the choice of mean, median, or mode depends on the nature of the data and the specific insights sought.

While commonly used for its simplicity, the  mean  has limitations, especially in the presence of outliers or skewed distributions. In such scenarios, the mean may not accurately represent the central tendency, as it is influenced by every value in the dataset, including the extreme ones.

With its resilience to outliers, the  median  often emerges as a more representative measure of central tendency, particularly in skewed distributions. It provides a more balanced central point by dividing a dataset into two halves, irrespective of extreme values.

The  mode , essential in categorical data analysis, illuminates the most frequently occurring value in a dataset. It is beneficial in identifying trends and commonalities within the data. However, its effectiveness may be limited in uniformly distributed datasets.

These measures have practical applications in a wide range of fields, from economics and finance to real estate and medicine. They aid in policy-making, investment decisions, market analysis, and much more, proving their indispensable role in various domains.

Recommended Articles

Discover more insights and in-depth analysis on statistical concepts by exploring related articles on our blog.

Which is Better, Mean or Median?

• Defining the Mean in Simple Terms!
• How to Calculate the Median in Excel

Frequently Asked Questions (FAQs)

Q1: What is Central Tendency?  Central tendency refers to the measure representing a dataset’s center or typical value.

Q2: How Do Mean, Median, and Mode Differ?  These measures differ in calculating the central value, each offering unique insights.

Q3: Why is the Mean Sensitive to Outliers?  The mean considers all data points, making it susceptible to extreme values.

Q4: In What Situation Is the Median Preferred?  The median is preferred in skewed distributions where outliers can distort the mean.

Q5: What is the Significance of Mode in Data Analysis?  Mode highlights the most frequently occurring data point, which is helpful in categorical analysis.

Q6: Can a Dataset Have More Than One Mode?  Yes, datasets can be bimodal or multimodal, having multiple modes.

Q7: How Does Skewness Affect Central Tendency Measures?  Skewness can make mean unrepresentative, often making median a better choice.

Q8: Why is Understanding Central Tendency Important?  It’s crucial for summarizing data and making informed decisions in analysis.

Q9: Can Central Tendency Measures be Misleading?  Yes, these measures can be deceptive without considering data distribution and outliers.

Q10: Where Can I Learn More About These Concepts?  Our blog and recommended readings offer deeper insights into these statistical measures.

Similar Posts

Explore the world of data interpretation with our blog, focusing on the key statistical measures — mean vs median. Understand their uses.

How to Calculate the Median in Excel – Simple Steps

Master How to Calculate Median in Excel with our step-by-step guide, enhancing your data analysis skills and understanding of central tendency.

Defining the Mean in Simple Terms! Mastering the Basics

Learn how to define the mean in simple terms and master the basics of this essential statistical concept for data analysis and interpretation.

What Is the Mode in a Data Set?

Explore the essence of ‘What Is the Mode in a Data Set’ and its pivotal role in statistical analysis for insightful data interpretation.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Mean, Median, Mode: An Introduction

• Reference work entry
• First Online: 01 January 2014
• Cite this reference work entry

• S. N. Gupta 2  

541 Accesses

1 Citations

Introduction

Mean, median and mode are three statistical measures commonly used to summarize data sets. They are known by the common name average . In its broadest sense, an average is simply any single value that is representative of many numbers. Averages are also called measures of central tendency because an average is usually located near the center of the data set. Some examples: average age of the players of a cricket team, average reaction time of a particular chemical, average amount spent by a customer in a shopping mall, etc.

The mean , also known as arithmetic mean , is the most widely used average and is defined as the sum of the observations divided by the number of observations. The formula for computing mean is: \(\bar{x}\) = (∑ x ) / n , where \(\bar{x}\) is the symbol for mean (pronounced “ x -bar”), x is the symbol for variable, ∑ x is the sum of observations (i.e., the sum of the values of the variable x ) and n is the number of observations.

Although, there are...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

References and Further Reading

Bluman AG (2007) Elementary statistics: a step by step approach, 6th edn. McGraw Hill, New York

Google Scholar  

Croucher JS (2002) Statistics: making business decisions. McGraw Hill/Irwin, New York

Mann PS (2006) Introductory statistics, 6th edn. Wiley, New York

Download references

Author information

Authors and affiliations.

University of South Pacific, Suva, Fiji

S. N. Gupta

You can also search for this author in PubMed   Google Scholar

Editor information

Editors and affiliations.

Department of Statistics and Informatics, Faculty of Economics, University of Kragujevac, City of Kragujevac, Serbia

Miodrag Lovric

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer-Verlag Berlin Heidelberg

About this entry

Cite this entry.

Gupta, S.N. (2011). Mean, Median, Mode: An Introduction. In: Lovric, M. (eds) International Encyclopedia of Statistical Science. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04898-2_353

Download citation

DOI : https://doi.org/10.1007/978-3-642-04898-2_353

Published : 02 December 2014

Publisher Name : Springer, Berlin, Heidelberg

Print ISBN : 978-3-642-04897-5

Online ISBN : 978-3-642-04898-2

eBook Packages : Mathematics and Statistics Reference Module Computer Science and Engineering

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Exploring Central Tendency: Mean, Median, and Mode

Have you ever wondered how researchers make sense of the vast amount of data they collect? Whether it’s customer satisfaction surveys or the results of a clinical trial, the key to unlocking the secrets of data often lies in finding its center. But what does that mean , and how do we find it? In the realm of statistics, this search for the center is encapsulated in the concept of central tendency , which is crucial for summarizing and describing data sets. Let’s delve into the three musketeers of central tendency: mean, median , and mode , and explore how each of them provides a unique perspective on our data’s central point.

Table of Contents

• What is Central Tendency and Why is it Important?
• The Arithmetic Mean: The Balancing Point of Data
• Calculating the Mean
• Pros and Cons of Using the Mean
• The Median: The Middleman of Data
• Identifying the Median
• Advantages and Disadvantages of the Median
• The Mode: The Popularity Contest Winner
• Finding the Mode
• The Mode’s Strengths and Weaknesses
• When to Use Mean, Median, and Mode

What is Central Tendency and Why is it Important? 🔗

Central tendency is a statistical measure that identifies a single value as representative of an entire distribution of data. It aims to provide a summary of a data set by pinpointing the central point around which all other data values cluster. This is paramount in research because it simplifies complex data sets, allowing us to make informed decisions and draw accurate conclusions. Imagine trying to understand the typical income of a group without central tendency; we’d be lost in a sea of individual numbers without a lighthouse to guide us.

The Arithmetic Mean: The Balancing Point of Data 🔗

The mean is perhaps the most familiar measure of central tendency. Often referred to as the average, it’s calculated by adding up all the values in a data set and dividing by the number of values. The result is the balancing point of the data set, where if the data were weights on a balance scale, the mean would be the fulcrum perfectly balancing them. The beauty of the mean lies in its sensitivity to each value in the data set, making it a comprehensive representation of the entire collection of numbers.

Calculating the Mean 🔗

Let’s say we have a data set representing the ages of a group of students: 17, 19, 20, 22, and 24. To find the mean, we add these numbers to get a total of 102. Dividing this by the number of values (5), we get a mean age of 20.4 years. Simple, right?

Pros and Cons of Using the Mean 🔗

• It incorporates all values in the data set, providing a comprehensive measure.
• It’s easy to compute and understand.
• It’s the basis for other statistical measures like variance and standard deviation .
• It’s sensitive to extreme values, or outliers , which can skew the mean.
• It may not accurately represent the typical value in a skewed distribution.

The Median: The Middleman of Data 🔗

While the mean considers every value, the median takes a different approach by identifying the middle value in a data set. To find the median, you arrange the data in ascending order and locate the value that falls right in the center. If the data set has an even number of values, the median is the average of the two central numbers. The median is like the mediator in a debate, ensuring that each side is equally represented without letting any single value dominate the discussion.

Identifying the Median 🔗

Using the same age data set, let’s find the median. Arranged in order, the ages are 17, 19, 20, 22, and 24. The middle value is 20, so the median age of the students is 20 years. If there had been another student aged, say, 25, the median would be the average of 20 and 22, resulting in 21 years.

Advantages and Disadvantages of the Median 🔗

Advantages:

• It’s unaffected by extreme scores or outliers.
• It provides a better measure of central tendency for skewed distributions than the mean.

Disadvantages:

• It may not consider the value of every data point, unlike the mean.
• It’s less useful for further statistical analysis.

The Mode: The Popularity Contest Winner 🔗

The mode is the value that occurs most frequently in a data set. It’s like the winner of a popularity contest, representing the choice or value with the highest number of votes. In some cases, a data set may have more than one mode, making it bimodal or multimodal , which signifies that there are multiple popular choices.

Finding the Mode 🔗

If we had a data set of ages with values like 20, 20, 22, 22, 22, and 24, the mode would be 22, as it appears more frequently than any other age. It’s worth noting that some data sets may not have a mode if no number repeats or if all numbers occur with the same frequency.

The Mode’s Strengths and Weaknesses 🔗

• It’s easy to identify.
• The mode can represent the most typical value in categorical data .

Weaknesses:

• It may not provide a clear picture of the data set’s central tendency if there are multiple modes.
• It’s not suitable for further statistical analysis.

When to Use Mean, Median, and Mode 🔗

The choice between mean, median, and mode depends on the nature of the data and the kind of information you seek. The mean is ideal for normally distributed data without outliers. The median is best for skewed distributions or when outliers are present. The mode is useful for categorical data and to identify the most common value. Knowing when to use each measure can help you better interpret and communicate your data’s story.

Conclusion 🔗

Understanding mean, median, and mode is like holding a compass that points to the heart of your data. Each measure of central tendency offers a different lens through which to view your data, providing insights into the general behavior and distribution of the variables under study. While they each have their strengths and weaknesses, together they form a triumvirate that can robustly summarize and describe data sets.

What do you think? Have you encountered situations where one measure of central tendency was more revealing than the others? Can you think of a scenario where it would be misleading to rely on just one of these measures?

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you!

Let us improve this post!

Tell us how we can improve this post?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Communication Research Methods

1 Research: Concept, Nature and Scope

• Research: Concept and Role
• Growth and Development
• Importance of Research
• Research: Nature and Characteristics
• Purpose of Research
• Scope of Communication Research

2 Classification of Research

• Based on Design
• Based on Stage
• Based on Nature
• Based on Location
• Based on Approach
• Communicators
• Media Content
• Distribution

3 Defining and Formulating Research Problems

• Difference between a Social Problem and a Research Problem
• Importance of Review of Literature
• Questions of Relevance, Feasibility, and Achievability
• Research Questions, Objectives, and Hypotheses
• Defining the Terms of Enquiry

4 Sampling Methods

• Types of Sampling
• Sampling Error
• Non-Probability Sampling
• Probability Sampling
• Sample Size

5 Review of Literature

• Literature Review: Need and Importance
• Objectives of Review of Literature
• Evaluation of Material for Review
• Writing Review of Literature

6 Data Collection Sources

• Primary and Secondary Data
• Sources of Secondary data
• Sources of Primary Data
• How to Store and Save Your Data

7 Survey Method

• Salient Features
• Types of Surveys
• Data collection tools
• Types of Questions
• Designing a Questionnaire
• The Process

8 Content Analysis

• Conceptual Foundations
• Characteristics of Content Analysis
• Types of Content Analysis
• Process of Content Analysis
• Let Us Sum Up

9 Experimental Method

• Nature of Experimental Method
• Classic Experimental Research Design
• Process of Experimental Research
• Experimental Design
• Field Experiments
• Merits and Demerits of Experimental Method

10 Interview Techniques

• Interview: Concept and Types
• Informal Interviews
• Structured Interviews
• Semi-structured Interviews
• Unstructured (Indepth) Interviews
• Interviewing Skills
• Ethical Issues

11 Case Study Method

• Case Study: A Qualitative Method
• Research Paradigms
• Main Features of Case Study Method
• Functions of Case Study
• Types of Case Studies
• Case Study Method: Strengths and Limitations
• The Process of Case Study

12 Observation Method

• Characteristics of Observation Method
• Strengths and Limitations
• Types of Observation
• Process of Observation
• Ethical Issues in Observation

13 Semiotics

• Texts and the Study of Signs
• Classification of Signs
• Paradigms and Syntagms
• Encoding and Decoding
• Social Semiotics

14 Basic Statistical Analysis

• Introduction to Statistics
• Populations and Samples
• Scales of Measurement
• Frequency Distribution
• Measures of Central Tendency
• Variability

15 Data Analysis

• Different Research Perspectives
• Handling Quantitative Data
• Qualitative Data Analysis
• Drawing Conclusion Through Data Analysis

16 Report Writing

• Stages in Report Writing
• The Beginning
• Main Body of the Report
• The Final Section
• Effective Writing

Share on Mastodon

• Science, Tech, Math ›
• Statistics ›

The Difference Between the Mean, Median, and Mode

• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Inferential Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

Measures of central tendency are numbers that describe what is average or typical within a distribution of data. There are three main measures of central tendency: mean, median , and mode. While they are all measures of central tendency, each is calculated differently and measures something different from the others.

The mean is the most common measure of central tendency used by researchers and people in all kinds of professions. It is the measure of central tendency that is also referred to as the average . A researcher can use the mean to describe the data distribution of  variables measured as intervals or ratios . These are variables that include numerically corresponding categories or ranges (like race , class, gender , or level of education), as well as variables measured numerically from a scale that begins with zero (like household income or the number of children within a family).

A mean is very easy to calculate. One simply has to add all the data values or "scores" and then divide this sum by the total number of scores in the distribution of data. For example, if five families have 0, 2, 2, 3, and 5 children respectively, the mean number of children is (0 + 2 + 2 + 3 + 5)/5 = 12/5 = 2.4. This means that the five households have an average of 2.4 children.

The median is the value at the middle of a distribution of data when those data are organized from the lowest to the highest value. This measure of central tendency can be calculated for variables that are measured with ordinal, interval or ratio scales.

Calculating the median is also rather simple. Let’s suppose we have the following list of numbers: 5, 7, 10, 43, 2, 69, 31, 6, 22. First, we must arrange the numbers in order from lowest to highest. The result is this: 2, 5, 6, 7, 10, 22, 31, 43, 69. The median is 10 because it is the exact middle number. There are four numbers below 10 and four numbers above 10.

If your data distribution has an even number of cases which means that there is no exact middle, you simply adjust the data range slightly in order to calculate the median. For example, if we add the number 87 to the end of our list of numbers above, we have 10 total numbers in our distribution, so there is no single middle number. In this case, one takes the average of the scores for the two middle numbers. In our new list, the two middle numbers are 10 and 22. So, we take the average of those two numbers: (10 + 22) /2 = 16. Our median is now 16.

The mode is the measure of central tendency that identifies the category or score that occurs the most frequently within the distribution of data. In other words, it is the most common score or the score that appears the highest number of times in a distribution. The mode can be calculated for any type of data, including those measured as nominal variables, or by name.

For example, let’s say we are looking at pets owned by 100 families and the distribution looks like this:

Animal     Number of families that own it

• Hamster: 13

The mode here is "dog" since more families own a dog than any other animal. Note that the mode is always expressed as the category or score, not the frequency of that score. For instance, in the above example, the mode is "dog," not 60, which is the number of times dog appears.

Some distributions do not have a mode at all. This happens when each category has the same frequency. Other distributions might have more than one mode. For example, when a distribution has two scores or categories with the same highest frequency, it is often referred to as " bimodal ."

• The Difference Between Descriptive and Inferential Statistics
• Empirical Relationship Between the Mean, Median, and Mode
• What Is Skewness in Statistics?
• Calculating the Mean Absolute Deviation
• A Introduction to Sociology Statistics
• What Is the Median?
• What Is Normal Distribution?
• Understanding Levels and Scales of Measurement in Sociology
• Calculating the Mean, Median, and Mode
• What Is the 5 Number Summary?
• What Are the First and Third Quartiles?
• When Is the Standard Deviation Equal to Zero?
• What Is the Midhinge?
• Exponential Distribution Medians
• What Is the Standard Normal Distribution?
• An Introduction to the Bell Curve

Descriptive Statistics: Measures Of Central Tendency (Mean, Median And Mode)

March 8, 2021 - paper 2 psychology in context | research methods.

• Back to Paper 2 - Research Methods

Quantitative Data Analysis Measures of Central Tendency (Description, AO1)

When you carry out a psychological experiment, you end up with a great deal of RAW DATA, usually in the form of 2 sets of scores one for each condition. The two sets of scores need to be compared to see if there is a noticeable difference between them. Often, you need to summarise this data so that you can easily see if your study has been successful.

A set of scores can be summarised by:- 1) A measure of  central tendency  (or  average ) of the scores. 2) A measure of the  dispersion  (or  spread ) of the scores. A measure of dispersion is a number which indicates how far each individual score (in the raw data set) is from the mean, (i.e. how far each score in the raw data set deviates from the mean).

There are  3 measures of central tendency:  the mean, median and mode.

1) MEAN (AO1)  This is calculated by adding up all the scores in a group/ in the raw data set and dividing it by the number of participants. It can only be used when the data is at interval level.

For example:  Imagine the following are scores from a memory test (out of 20) obtained from a group of teenagers (age 13 to 19 inclusive);

19, 18, 19, 20, 15, 16, 11, 14, 12, 19, 18, 19, 17, 12 (there are 14 participants in this research study)

In order to calculate the mean of these scores (the average memory performance of teenagers aged 13 to 19 in this study), we need to add all the above scores. This gives us a total of 229

In order to calculate the mean, the total of the scores (229) needs to be divided by the number of participants in the study, which in this case is 14.

229/14 = 16.4, therefore, the  mean  memory performance in this study is  16.4 .

Evaluation (AO3) of the Mean as a Measure of Central Tendency 

Strength of using the Mean:

POINT:  The mean can be considered an accurate and sensitive measure of the average of a set of scores.                                                                                                                                          EXAMPLE:  For example,  the mean takes all the scores in the data set into consideration.  ELABORATION:  This is a strength because,  due to the fact that all the scores are taken into consideration, it can be seen that the mean is a highly representative measure of central tendency and therefore is an accurate representation of the whole data set.

Weakness of using the Mean:

POINT:  A weakness of using the mean is that it can be influenced by rogue scores.              EXAMPLE:   For example,  in a set of data with similar scores (e.g. 13, 12, 11, 10 etc ) a score like 5 can be seen as a rogue score that will significantly lower the average (mean) calculation.                                                                                                                                                ELABOATION:   This is a weakness because,  rogue scores in the data set can significantly increase/ reduce the calculated mean score making it unreflective/unrepresentative of the raw data set.

2) MEDIAN (AO1)    This is the middle score. It is calculated by putting the scores in numerical order and finding the middle value. If there is an even number of scores, the two middle scores are averaged to find the median. It can only be used when the data is of at least ordinal level.

For example,  in order to calculate the mean of the data below

19, 18, 19, 20, 15, 16, 11, 14, 12, 19, 18, 19, 17, 12 the scores are first arranged in ascending order,

11, 12, 12, 14, 15, 16, 17, 18, 18, 19, 19, 19, 19, 20 now the middle  (median) value  of this data set can be established which, in this case is  17.5.

Evaluation (AO3) of the Median as a Measure of Central Tendency 

Strength  of using the Median: POINT:  A strength of using the median is that it is unaffected by extreme, rogue scores.    EXAMPLE:   For example,  the median is only concerned with the middle number in a set of raw data, it doesn’t consider any of the other scores.                                                                 ELABOATION:  This is a strength because,  only considering the middle score means that any other scores (in particular, rogue/extreme scores) are ignored, this makes the median more representative of the whole data set and therefore, the median can be said to be an accurate measure of central tendency.

Weakness of using the Median: POINT:  A weakness of using the median is that it doesn’t take all the scores in the data set into consideration.                                                                                                         EXAMPLE:  For example, the median is only concerned with the middle number in a set of raw data, it doesn’t consider any of the other scores.                                                                 ELABOATION:  This is a weakness because, only considering the middle score means that all other scores in the data set are ignored, from this, the accuracy of the median can be questioned how can this be an accurate measure of central tendency if it doesn’t take all the scores in the data set into consideration?

3) MODE (AO1)-  This is the most common score/the score that appears the most in a set of raw data. It can be used with any level of data, because it requires only at least nominal data.

For example, in the following set of data:

19, 18, 19, 20, 15, 16, 11, 14, 12, 19, 18, 19, 17, 12 the  mode  is  19.  This is because the number 19 appears more frequently than any other in this set of data.

Evaluation (AO3) of the Mode as a Measure of Central Tendency

Strength of using the Mode:                                                                                                                                                                                                                                                                        POINT:  A strength of using the mode is that it is unaffected by extreme, rogue scores.    EXAMPLE:  For example, the mode is only concerned with the most frequently occurring number in a set of raw data, it doesn’t consider any of the other scores.                                  ELABOATION:  This is a strength because, only considering the most frequently occurring number means that any other scores (in particular, rogue/extreme scores) are ignored, this makes the mode more representative of the whole data set and therefore, the mode can be said to be an accurate measure of central tendency.

Weakness of using the Mode:                                                                                                                         POINT:  A weakness of using the mode is that it doesn’t take all the scores in the data set into consideration.                                                                                                                EXAMPLE:  For example, the mode is only concerned with the most frequently occurring number in a set of raw data, it doesn’t consider any of the other scores.                                   ELABOATION:  This is a weakness because, only considering the most frequently occurring score means that all other scores in the data set are ignored, from this, the accuracy of the mode can be questioned how can this be an accurate measure of central tendency if it doesn’t take all the scores in the data set into consideration?

• Psychopathology
• Social Psychology
• Approaches To Human Behaviour
• Biopsychology
• Research Methods
• Issues & Debates
• Teacher Hub
• Terms and Conditions
• Privacy Policy
• Cookie Policy
• [email protected]
• www.psychologyhub.co.uk

We're not around right now. But you can send us an email and we'll get back to you, asap.

Start typing and press Enter to search

Cookie Policy - Terms and Conditions - Privacy Policy