the quantum physics experiment

September 30, 2024

Evidence of ‘Negative Time’ Found in Quantum Physics Experiment

Physicists showed that photons can seem to exit a material before entering it, revealing observational evidence of negative time

By Manon Bischoff & Jeanna Bryner

Time can take on negative values in the quantum realm.

Sean Gladwell/Getty Images

Quantum physicists are familiar with wonky, seemingly nonsensical phenomena: atoms and molecules sometimes act as particles, sometimes as waves; particles can be connected to one another by a “spooky action at a distance,” even over great distances; and quantum objects can detach themselves from their properties like the Cheshire Cat from Alice’s Adventures in Wonderland detaches itself from its grin. Now researchers led by Daniela Angulo of the University of Toronto have revealed another oddball quantum outcome: photons, wave-particles of light , can spend a negative amount of time zipping through a cloud of chilled atoms. In other words, photons can seem to exit a material before entering it.

“It took a positive amount of time , but our experiment observing that photons can make atoms seem to spend a *negative* amount of time in the excited state is up!” wrote Aephraim Steinberg, a physicist at the University of Toronto, in a post on X (formerly Twitter) about the new study , which was uploaded to the preprint server arXiv.org on September 5 and has not yet been peer-reviewed.

The idea for this work emerged in 2017. At the time, Steinberg and a lab colleague, then doctoral student Josiah Sinclair, were interested in the interaction of light and matter, specifically a phenomenon called atomic excitation : when photons pass through a medium and get absorbed, electrons swirling around atoms in that medium jump to higher energy levels. When these excited electrons lapse to their original state, they release that absorbed energy as reemitted photons, introducing a time delay in the light’s observed transit time through the medium.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

Sinclair’s team wanted to measure that time delay (which is sometimes technically called a “group delay”) and learn whether it depends on the fate of that photon: Was it scattered and absorbed inside the atomic cloud, or was it transmitted with no interaction whatsoever? “At the time, we weren’t sure what the answer was, and we felt like such a basic question about something so fundamental should be easy to answer,” Sinclair says. “But the more people we talked to, the more we realized that while everyone had their own intuition or guess, there was no expert consensus on what the right answer would be.” Because the nature of these delays can be so strange and counterintuitive, some researchers had written the phenomenon off as effectively meaningless for describing any physical property associated with light.

After three years of planning, his team developed an apparatus to test this question in the lab. Their experiments involved shooting photons through a cloud of ultracold rubidium atoms and measuring the resulting degree of atomic excitation. Two surprises emerged from the experiment : Sometimes photons would pass through unscathed, yet the rubidium atoms would still become excited—and for just as long as if they had absorbed those photons. Stranger still, when photons were absorbed, they would seem to be reemitted almost instantly, well before the rubidium atoms returned to their ground state—as if the photons, on average, were leaving the atoms quicker than expected.

The team then collaborated with Howard Wiseman, a theoretical and quantum physicist at Griffith University in Australia, to devise an explanation. The theoretical framework that emerged showed that the time these transmitted photons spent as an atomic excitation matched perfectly with the expected group delay acquired by the light—even for cases where it seemed as though the photons were reemitted before the atomic excitation had ebbed.

To understand the nonsensical finding, you can think of photons as the fuzzy quantum objects they are, in which any given photon’s absorption and reemission through an atomic excitation is not guaranteed to occur over a certain fixed amount of time; rather, it takes place across a smeared-out, probabilistic range of temporal values. As demonstrated by the team’s experiments, these values can encompass instances when an individual photon’s transit time is instantaneous—or, bizarrely, when it concludes before the atomic excitation has ceased, which gives a negative value.

“I can promise you that we were completely surprised by this prediction,” Sinclair says, referring to the matchup between the group delay and the time that the transmitted photons spent as atomic excitations. “And as soon as we were confident we hadn’t made a mistake, Steinberg and the rest of the team—I had moved on to do a postdoc at [the Massachusetts Institute of Technology] by this point—began planning to do a follow-up experiment to test this crazy prediction of negative dwell time and see if the theory would hold up.”

That follow-up experiment, the one led by Angulo that Steinberg touted on X, can be understood by considering the two ways a photon can be transmitted. In one, the photon wears blinders of sorts and ignores the atom entirely, leaving without even a nod. In the other, it interacts with the atom, boosting it to a higher energy level, before getting reemitted.

“When you see a transmitted photon, you can’t know which of these occurred,” Steinberg says, adding that because photons are quantum particles in the quantum realm, the two outcomes can be in superposition —both things can happen at the same time. “The measuring device ends up in a superposition of measuring zero and measuring some small positive value.” But correspondingly, Steinberg notes, that also means that sometimes “the measuring device ends up in a state that looks not like ‘zero’ plus ‘something positive’ but like ‘zero’ minus ‘something positive,’ resulting in what looks like the wrong sign, a negative value, for this excitation time.”

The measurement results in Angulo and her colleagues’ experiment suggest that the photons moved through the medium faster when they excited the atoms than when the atoms remained in their ground state. (The photons aren’t communicating any information, so the outcome does not contradict the “nothing can travel faster than light” speed limit set by Einstein’s special theory of relativity .)

“A negative time delay may seem paradoxical, but what it means is that if you built a ‘quantum’ clock to measure how much time atoms are spending in the excited state, the clock hand would, under certain circumstances, move backward rather than forward,” Sinclair says. In other words, the time in which the photons were absorbed by atoms is negative.

Even though the phenomenon is astonishing, it has no impact on our understanding of time itself—but it does illustrate once again that the quantum world still has surprises in store.

“[Angulo] and the rest of the team have accomplished something really impressive and produced a beautiful set of measurements. Their results raise interesting questions about the history of photons traveling through absorptive media and necessitate a reinterpretation of the physical meaning of the group delay in optics,” Sinclair says.

A version of this article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

What Is Quantum Physics?

Quantum physics is the study of matter and energy at the most fundamental level. It aims to uncover the properties and behaviors of the very building blocks of nature.

While many quantum experiments examine very small objects, such as electrons and photons, quantum phenomena are all around us, acting on every scale. However, we may not be able to detect them easily in larger objects. This may give the wrong impression that quantum phenomena are bizarre or otherworldly. In fact, quantum science closes gaps in our knowledge of physics to give us a more complete picture of our everyday lives.

Quantum discoveries have been incorporated into our foundational understanding of materials, chemistry, biology, and astronomy. These discoveries are a valuable resource for innovation, giving rise to devices such as lasers and transistors, and enabling real progress on technologies once considered purely speculative, such as quantum computers . Physicists are exploring the potential of quantum science to transform our view of gravity and its connection to space and time. Quantum science may even reveal how everything in the universe (or in multiple universes) is connected to everything else through higher dimensions that our senses cannot comprehend.

The Origins of Quantum Physics

The field of quantum physics arose in the late 1800s and early 1900s from a series of experimental observations of atoms that didn't make intuitive sense in the context of classical physics. Among the basic discoveries was the realization that matter and energy can be thought of as discrete packets, or quanta, that have a minimum value associated with them. For example, light of a fixed frequency will deliver energy in quanta called "photons." Each photon at this frequency will have the same amount of energy, and this energy can't be broken down into smaller units. In fact, the word "quantum" has Latin roots and means "how much."

Knowledge of quantum principles transformed our conceptualization of the atom, which consists of a nucleus surrounded by electrons. Early models depicted electrons as particles that orbited the nucleus, much like the way satellites orbit Earth. Modern quantum physics instead understands electrons as being distributed within orbitals, mathematical descriptions that represent the probability of the electrons' existence in more than one location within a given range at any given time. Electrons can jump from one orbital to another as they gain or lose energy, but they cannot be found between orbitals.

Other central concepts helped to establish the foundations of quantum physics:

• Wave-particle duality: This principle dates back to the earliest days of quantum science. It describes the outcomes of experiments that showed that light and matter had the properties of particles or waves, depending on how they were measured. Today, we understand that these different forms of energy are actually neither particle nor wave. They are distinct quantum objects that we cannot easily conceptualize.
• Superposition : This is a term used to describe an object as a combination of multiple possible states at the same time. A superposed object is analogous to a ripple on the surface of a pond that is a combination of two waves overlapping. In a mathematical sense, an object in superposition can be represented by an equation that has more than one solution or outcome.
• Uncertainty principle : This is a mathematical concept that represents a trade-off between complementary points of view. In physics, this means that two properties of an object, such as its position and velocity, cannot both be precisely known at the same time. If we precisely measure the position of an electron, for example, we will be limited in how precisely we can know its speed.
• Entanglement : This is a phenomenon that occurs when two or more objects are connected in such a way that they can be thought of as a single system, even if they are very far apart. The state of one object in that system can't be fully described without information on the state of the other object. Likewise, learning information about one object automatically tells you something about the other and vice versa.

Mathematics and the Probabilistic Nature of Quantum Objects

Because many of the concepts of quantum physics are difficult if not impossible for us to visualize, mathematics is essential to the field. Equations are used to describe or help predict quantum objects and phenomena in ways that are more exact than what our imaginations can conjure.

Mathematics is also necessary to represent the probabilistic nature of quantum phenomena. For example, the position of an electron may not be known exactly. Instead, it may be described as being in a range of possible locations (such as within an orbital), with each location associated with a probability of finding the electron there.

Given their probabilistic nature, quantum objects are often described using mathematical "wave functions," which are solutions to what is known as the Schrödinger equation . Waves in water can be characterized by the changing height of the water as the wave moves past a set point. Similarly, sound waves can be characterized by the changing compression or expansion of air molecules as they move past a point. Wave functions don't track with a physical property in this way. The solutions to the wave functions provide the likelihoods of where an observer might find a particular object over a range of potential options. However, just as a ripple in a pond or a note played on a trumpet are spread out and not confined to one location, quantum objects can also be in multiple places—and take on different states, as in the case of superposition—at once.

Observation of Quantum Objects

The act of observation is a topic of considerable discussion in quantum physics. Early in the field, scientists were baffled to find that simply observing an experiment influenced the outcome. For example, an electron acted like a wave when not observed, but the act of observing it caused the wave to collapse (or, more accurately, "decohere") and the electron to behave instead like a particle. Scientists now appreciate that the term "observation" is misleading in this context, suggesting that consciousness is involved. Instead, "measurement" better describes the effect, in which a change in outcome may be caused by the interaction between the quantum phenomenon and the external environment, including the device used to measure the phenomenon. Even this connection has caveats, though, and a full understanding of the relationship between measurement and outcome is still needed.

The Double-Slit Experiment

Perhaps the most definitive experiment in the field of quantum physics is the double-slit experiment . This experiment, which involves shooting particles such as photons or electrons through a barrier with two slits, was originally used in 1801 to show that light is made up of waves. Since then, numerous incarnations of the experiment have been used to demonstrate that matter can also behave like a wave and to demonstrate the principles of superposition, entanglement, and the observer effect.

The field of quantum science may seem mysterious or illogical, but it describes everything around us, whether we realize it or not. Harnessing the power of quantum physics gives rise to new technologies, both for applications we use today and for those that may be available in the future .

Dive Deeper

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• BOOKS AND ARTS
• 07 August 2018

Two slits and one hell of a quantum conundrum

• Philip Ball 0

Philip Ball is a writer based in London.

You can also search for this author in PubMed   Google Scholar

You have full access to this article via your institution.

Bands of light in a double-slit experiment. Credit: Timm Weitkamp/CC BY 3.0

Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality Anil Ananthaswamy Dutton (2018)

According to the eminent physicist Richard Feynman, the quantum double-slit experiment puts us “up against the paradoxes and mysteries and peculiarities of nature”. By Feynman’s logic, if we could understand what is going on in this deceptively simple experiment, we would penetrate to the heart of quantum theory — and perhaps all its puzzles would dissolve.

That’s the premise of Through Two Doors at Once . Science writer Anil Ananthaswamy focuses on this single experiment, which has taken many forms since quantum mechanics debuted in the early twentieth century with the work of Max Planck, Albert Einstein, Niels Bohr and others. In some versions, nature seems magically to discern our intentions before we enact them — or perhaps retroactively to alter the past. In others, the outcome seems dependent on what we know, not what we do. In yet others, we can deduce something about a system without looking at it. All in all, the double-slit experiment seems, to borrow from Feynman again, “screwy”.

The original experiment, as Ananthaswamy notes, was classical, conducted by British polymath Thomas Young in the early 1800s to show that light is a wave. He passed light through two closely spaced parallel slits in a screen, and on the far side saw several bright bands. This, he realized, was an ‘interference’ pattern. Caused by the interaction of waves emanating from the openings, it’s not unlike the pattern that appears when two pebbles are dropped into water and the ripples they create add to or dampen each other’s peaks and troughs. With ordinary particles, the slits would act more like stencils for sprayed paint, creating two defined bands.

We now know that quantum particles create such an interference pattern, too — evidence that they have a wave-like nature. Postulated in 1924 by French physicist Louis de Broglie, this idea was verified for electrons a few years later by US physicists Clinton Davisson and Lester Germer. Even large molecules such as buckminsterfullerene — made of 60 carbon atoms — will behave in this way.

You can get used to that. What’s odd is that the interference pattern remains — accumulating over many particle impacts — even if particles go through the slits one at a time. The particles seem to interfere with themselves. Odder, the pattern vanishes if we use a detector to measure which slit the particle goes through: it’s truly particle-like, with no more waviness. Oddest of all, that remains true if we delay the measurement until after the particle has traversed the slits (but before it hits the screen). And if we make the measurement but then delete the result without looking at it, interference returns.

It’s not the physical act of measurement that seems to make the difference, but the “act of noticing”, as physicist Carl von Weizsäcker (who worked closely with quantum pioneer Werner Heisenberg) put it in 1941. Ananthaswamy explains that this is what is so strange about quantum mechanics: it can seem impossible to eliminate a decisive role for our conscious intervention in the outcome of experiments. That fact drove physicist Eugene Wigner to suppose at one point that the mind itself causes the ‘collapse’ that turns a wave into a particle.

Ananthaswamy offers some of the most lucid explanations I’ve seen of other interpretations. Bohr’s answer was that quantum mechanics doesn’t let us say anything about the particle’s ‘path’ — one slit or two — before it is measured. The role of the theory, said Bohr, is to furnish predictions of measurement outcomes; in that regard, it has never been found to fail. (However, he did not, as is often implied, deny that there is any physical reality beyond measurement.) Yet this does feel rather unsatisfactory. Ananthaswamy seems tempted by the alternative idea offered by David Bohm in the 1950s. Here, quantum objects are both particle and wave, the wave somehow ‘piloting’ the particle through space while being sensitive to influences beyond the particle’s location. But Ananthaswamy concludes that “physics has yet to complete its passage through the double-slit experiment. The case remains unsolved.”

With apologies to researchers convinced that they have the answer, this is true: there is no consensus. At any rate, Bohr was right to advise caution in how we use language. There is nothing in quantum mechanics as it stands, shorn of interpretation, that lets us speak of particles becoming waves or taking two paths at once. And there is no reason to regard the wavefunction as more or less than an abstraction. This mathematical function, which embodies all we can know about a quantum object (and features in the iconic equation devised by Erwin Schrödinger to describe the object’s wave-like behaviour) was characterized rather nicely by physicist Roland Omnès. He called it “the fuel of a machine that manufactures probabilities” — that is, probabilities of measurement outcomes.

Refracting all of quantum mechanics through the double slits is both a strength and a weakness of Through Two Doors at Once . It brings unity to a knotty subject, but downplays some important strands. Those include John Bell’s 1964 thought experiment on the nature of quantum entanglement (conducted for real many times since the 1970s); the role of decoherence in the emergence of classical physics from quantum phenomena (adduced in the 1970s and 1980s); and the emphasis on information and causality in the past two decades. Still, given that popularization of quantum mechanics seems to be the flavour of the month — summoning Adam Becker’s 2018 book What is Real? , Jean Bricmont’s 2017 Quantum Sense and Nonsense , a forthcoming book by physicist Sean Carroll, and my own 2018 Beyond Weird — there’s no lack of a wider perspective.

And we need that. Ananthaswamy’s conclusion — that perhaps all the major interpretations are “touching the truth in their own way” — is not a shrugging capitulation. It’s a well-advised commitment to pluralism, shared with Becker’s book and mine. For now, uncertainty seems the wisest position in the quantum world.

Nature 560 , 165 (2018)

doi: https://doi.org/10.1038/d41586-018-05892-6

Related Articles

• Quantum physics

Entanglement and iSWAP gate between molecular qubits

Article 13 NOV 24

Observation of Hilbert space fragmentation and fractonic excitations in 2D

Physicists tame fundamental muon particles into highly controlled beam for first time

News 24 OCT 24

Growth area: early studies exploring how tissues and cells grow

News & Views 12 NOV 24

First DNA from Pompeii body casts illuminates who victims were

News 07 NOV 24

How fungus-farming ants have nourished biology for 150 years

Correspondence 05 NOV 24

Al Medical Engineering at School of Biomedical Engineering

Tsinghua BME offers faculty positions in the emerging research direction of AI Medical Engineering

Beijing, China

Tsinghua University

Faculty Positions at the Center for Advanced Microbiome Research

Faculty Positions in Microbiome Research at the Center for Advanced Microbiome Research and Innovation, Institute for Genome Sciences, UM SOM

Baltimore, Maryland

Institute for Genome Sciences, University of Maryland School of Medicine

Senior Publisher

The Senior Publisher will support a portfolio of open access journals including journals in the life, biomedical, and health sciences.

London Heidelberg or Milan – Hybrid working model

Springer Nature Ltd

Associate / or Senior News & Views Editor (Physics)

Job Title:  Associate / or Senior News & Views Editor (Physics) (m/w/d) Full Time, Permanent Location(s):    London, Berlin   Closing date: 5th Dec...

London (Central), London (Greater) (GB)

Associate Senior Lecturer in Molecular Medicine: regenerative medicine and disease mechanisms

In this call for proposals (Wallenberg Molecular Medicine Fellow), we are looking for prominent researchers with international research experience.

Lund, Skåne (SE)

Lund University

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• Collections

• APS Journals

Nobel Prize : Quantum Entanglement Unveiled

7 October 2022: We have replaced our initial one-paragraph announcement with a full-length Focus story.

The Nobel Prize in Physics this year recognizes efforts to take quantum weirdness out of philosophy discussions and to place it on experimental display for all to see. The award is shared by Alain Aspect, John Clauser, and Anton Zeilinger, all of whom showed a mastery of entanglement—a quantum relationship between two particles that can exist over long distances. Using entangled photons, Clauser and Aspect performed some of the first “Bell tests,” which confirmed quantum mechanics predictions while putting to bed certain alternative theories based on classical physics. Zeilinger used some of those Bell-test techniques to demonstrate entanglement control methods that can be applied to quantum computing, quantum cryptography, and other quantum information technologies.

Since its inception, quantum mechanics has been wildly successful at predicting the outcomes of experiments. But the theory assumes that some properties of a particle are inherently uncertain—a fact that bothered many physicists, including Albert Einstein. He and his colleagues expressed their concern in a paradox they described in 1935 [ 1 ]: Imagine creating two quantum mechanically entangled particles and distributing them between two separated researchers, characters later named Alice and Bob. If Alice measures her particle, then she learns something about Bob’s particle—as if her measurement instantaneously changed the uncertainty about the state of his particle. To avoid such “spooky action at a distance,” Einstein proposed that lying underneath the quantum framework is a set of classical “hidden variables” that determine precisely how a particle will behave, rather than providing only probabilities.

The hidden variables were unmeasurable—by definition—so most physicists deemed their existence to be a philosophical issue, not an experimental one. That changed in 1964 when John Bell of the University of Wisconsin-Madison, proposed a thought experiment that could directly test the hidden variable hypothesis [ 2 ]. As in Einstein’s paradox, Alice and Bob are each sent one particle of an entangled pair. This time, however, the two researchers measure their respective particles in different ways and compare their results. Bell showed that if hidden variables exist, the experimental results would obey a mathematical inequality. However, if quantum mechanics was correct, the inequality would be violated.

Bell’s work showed how to settle the debate between quantum and classical views, but his proposed experiment assumed detector capabilities that weren’t feasible. A revised version using photons and polarizers was proposed in 1969 by Clauser, then at Columbia University, along with his colleagues [ 3 ]. Three years later, Clauser and Stuart Freedman (both at the University of California, Berkeley) succeeded in performing that experiment [ 4 ].

The Freedman-Clauser experiment used entangled photons obtained by exciting calcium atoms. When a calcium atom de-excites, it can emit two photons whose polarizations are aligned. The researchers installed two detectors (Alice and Bob) on opposite sides of the calcium source and measured the rate of coincidences—two photons hitting the detectors simultaneously. Each detector was equipped with a polarizer that could be rotated to an arbitrary orientation.

Freedman and Clauser showed theoretically that quantum mechanics predictions diverge strongly from hidden variable predictions when Alice and Bob’s polarizers are offset from each other by 22.5° or 67.5°. The researchers collected 200 hours of data and found that the coincidence rates violated a revamped Bell’s inequality, proving that quantum mechanics is right.

The results of the first Bell test were a blow to hidden variables, but there were “loopholes” that hidden-variable supporters could claim to rescue their theory. One of the most significant loopholes was based on the idea that the setting of Alice’s polarizer could have some influence on Bob’s polarizer or on the photons that are created at the source. Such effects could allow the elements of a hidden-variable system to “conspire” together to produce measurement outcomes that mimic quantum mechanics.

To close this so-called locality loophole, Aspect and his colleagues at the Institute of Optics Graduate School in France performed an updated Bell test in 1982, using an innovative method for randomly changing the polarizer orientations [ 5 ]. The system worked like a railroad switch, rapidly diverting photons between two separate “tracks,” each with a different polarizer. The changes were made as the photons were traveling from the source to the detectors, so there was not enough time for coordination between supposed hidden variables.

Zeilinger, who is now at the University of Vienna, has also worked on removing loopholes from Bell tests (see Viewpoint: Closing the Door on Einstein and Bohr’s Quantum Debate , written by Aspect). In 2017, for example, he and his collaborators devised a way to use light from distant stars as a random input for setting polarizer orientations (see Synopsis: Cosmic Test of Quantum Mechanics ).

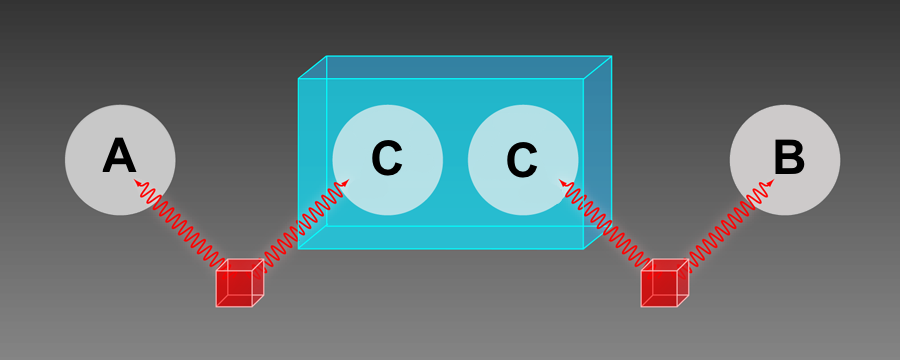
Zeilinger also used the techniques of entanglement control to explore practical applications, such as quantum teleportation and entanglement swapping. For the latter, he and his team showed in 1998 that they could create entanglement between two photons that were never in contact [ 6 ]. In this experiment, two sets of entangled photon pairs are generated at two separate locations. One from each pair is sent to Alice and Bob, while the other two photons are sent to a third person, Cecilia. Cecilia performs a Bell-like test on her two photons, and when she records a particular result, Alice’s photon winds up being entangled with Bob's. This swapping could be used to send entanglement over longer distances than is currently possible with optical fibers (see Research News: The Key Device Needed for a Quantum Internet ).

“Quantum entanglement is not questioned anymore,” says quantum physicist Jean Dalibard from the College of France. “It has become a tool, in particular in the emerging field of quantum information processing, and the three nominated scientists can be considered as the godfathers of this new domain.”

Quantum information specialist Jian-Wei Pan of the University of Science and Technology of China in Hefei says the winners are fully deserving of the prize. He has worked with Zeilinger on several projects, including a quantum-based satellite link (see Focus: Intercontinental, Quantum-Encrypted Messaging and Video ). “Now, in China, we are putting a lot of effort into actually turning these dreams into reality, hoping to make the quantum technologies practically useful for our society.”

–Michael Schirber

Michael Schirber is a Corresponding Editor for  Physics Magazine based in Lyon, France.

• A. Einstein et al. , “Can quantum-mechanical description of physical reality be considered complete?” Phys. Rev. 47 , 777 (1935) .
• J. S. Bell, “On the Einstein Podolsky Rosen paradox,” Physics 1 , 195 (1964) .
• J. F. Clauser et al. , “Proposed experiment to test local hidden-variable theories,” Phys. Rev. Lett. 23 , 880 (1969) .
• S. J. Freedman and J. F. Clauser, “Experimental test of local hidden-variable theories,” Phys. Rev. Lett. 28 , 938 (1972) .
• A. Aspect et al. , “Experimental test of Bell’s inequalities using time-varying analyzers,” Phys. Rev. Lett. 49 , 1804 (1982) .
• J. W. Pan et al. , “Experimental entanglement swapping: Entangling photons that never interacted,” Phys. Rev. Lett. 80 , 3891 (1998) .

More Information

Research News: Hiding Secrets Using Quantum Entanglement

Research News: Diagramming Quantum Weirdness

APS press release

The Nobel Prize in Physics 2022 (Nobel Foundation)

Experimental Test of Bell's Inequalities Using Time-Varying Analyzers

Alain Aspect, Jean Dalibard, and Gérard Roger

Phys. Rev. Lett. 49 , 1804 (1982)

Published December 20, 1982

Experimental Entanglement Swapping: Entangling Photons That Never Interacted

Jian-Wei Pan, Dik Bouwmeester, Harald Weinfurter, and Anton Zeilinger

Phys. Rev. Lett. 80 , 3891 (1998)

Published May 4, 1998

Experimental Test of Local Hidden-Variable Theories

Stuart J. Freedman and John F. Clauser

Phys. Rev. Lett. 28 , 938 (1972)

Published April 3, 1972

Subject Areas

Related articles.

Quantifying the Background Radiation Hitting Superconducting Qubits

Researchers have characterized the naturally occurring background radiation hitting a typical quantum circuit—a result that might help with the engineering of devices that are less vulnerable to radiation-induced decoherence. Read More »

How to Move Multiple Ions in Two Dimensions

A scheme that moves electromagnetically trapped ions around a 2D array of sites could aid development of scaled-up ion-based quantum computing. Read More »

Can Classical Worlds Emerge from Parallel Quantum Universes?

Simulations deliver hints on how the multiverse produced according to the many-worlds interpretation of quantum mechanics might be compatible with our stable, classical Universe. Read More »

Sign up to receive weekly email alerts from Physics Magazine .

IBM's newest 156-qubit quantum chip can run 50 times faster than its predecessor — equipping it for scientific research

When combined with Qiskit software tools, the 156-qubit R2 Heron quantum processor can perform 5,000 two-qubit gate operations — double the previous best — meaning it's ready for complex quantum computations, IBM scientists say.

IBM's latest quantum computer is now powerful enough for useful scientific research , scientists say, after the company made significant hardware and software improvements to its quantum system.

The new system is made of two parts: a new 156-qubit quantum processing unit (QPU) called R2 IBM Heron (the second generation of a chip launched last year) ; and Qiskit — a collection of software tools and algorithms designed to optimize quantum computing performance.

The result is a new system that can perform tasks up to 50 times faster than previous efforts, according to benchmarking data . For reference, in IBM's 2023 quantum utility experiment, published in the journal Nature , its most powerful quantum computer at the time took 122 hours to run workloads in the benchmark. The new system, fitted with the R2 Heron QPU, took just 2.4 hours.

The new quantum computers, based in IBM's data centers based around the world can tackle scientific problems across materials, chemistry, life sciences, high-energy physics and more domains, IBM representatives said in a statement .

Related: New 'gold-plated' superconductor could be the foundation for massively scaled-up quantum computers in the future

"Advances across IBM Quantum hardware and Qiskit are enabling our users to build new algorithms in which advanced quantum and classical supercomputing resources can be knit together to combine their respective strengths," Jay Gambetta , vice president for IBM Quantum, said in the statement.

Next-generation quantum processing

The R2 Heron QPU is fitted with 156 qubits arranged in a heavy-hexagonal lattice — a topological structure that IBM uses for all its quantum processors. This enables the system to reliably execute quantum circuits of up to 5,000 two-qubit gates — which is nearly double the 2,880 two-qubit gates in the 2023 utility experiment, powered by the 127-qubit Eagle QPU.

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

Two-qubit gates are essential to unlocking the exponential power of a quantum computer — in which the more qubits there are fitted into a system, the more calculations can run in parallel. Single qubit gates allow for individual qubits to rotate or flip their states, while two-qubit gates operating in pairs of qubits tap into the laws of quantum mechanics to enable entanglement between them. While single-qubit gates can function on a basic level, utilizing two-qubit gates can enable a quantum computer to perform far more complex calculations.

The new R2 Heron chip also features "two-level system mitigation," which helps to reduce the impact of disturbances to the qubits interacting with the materials surrounding them. The system also benefits from software improvements to error correction — namely, the use of Qiskit's tensor error network mitigation algorithm (TEM).

Further software improvements, including the launch of the latest generation of the runtime engine, optimizing data movement and the introduction of parametric compiling , mean the new system can run at 150,000 circuit layer operations per second (CLOPS). In comparison, base performance was just 950 CLOPS in 2022 and 37,000 CLOPS earlier this year when optimizing data movement was first introduced.

Quantum-centric supercomputing

IBM representatives claim that the latest developments feed into their vision of developing "quantum-centric" supercomputers — which combine quantum and classical computers to achieve viable results sooner than they would by using only quantum computers. .

— Will we ever have quantum laptops?

— Quantum computing breakthrough could happen with just hundreds, not millions, of qubits using new error-correction system

— Scientists build the smallest quantum computer in the world — it works at room temperature and you can fit it on your desk

This is because hybrid systems can address workloads in parallel, breaking down complex algorithms by assigning parts of the task to the half of the system for which they are best suited. Once these chunks are solved, the software layer seamlessly stitches the problems back together.

An example of quantum-centric supercomputing in action is at RIKEN, a scientific research center in Japan. Using a method known as "Quantum-Selected Configuration Interaction," outlined in a paper published to the arXiv preprint database in 2023, scientists are using quantum hardware to model the electronic structure of iron sulfides .

Scientists at RIKEN have also embarked on a project to build a quantum-high-performance-computing hybrid platform by integrating Fugaku, one of the world's fastest supercomputers , with an on-premises IBM System Two quantum computer powered by the Heron QPU.

Keumars is the technology editor at Live Science. He has written for a variety of publications including ITPro, The Week Digital, ComputerActive, The Independent, The Observer, Metro and TechRadar Pro. He has worked as a technology journalist for more than five years, having previously held the role of features editor with ITPro. He is an NCTJ-qualified journalist and has a degree in biomedical sciences from Queen Mary, University of London. He's also registered as a foundational chartered manager with the Chartered Management Institute (CMI), having qualified as a Level 3 Team leader with distinction in 2023.

New 'gold-plated' superconductor could be the foundation for massively scaled-up quantum computers in the future

Will we ever have quantum laptops?

Researchers spot rare 'triple-ring' galaxy that defies explanation

Most Popular

• 2 'Missing link' found in ancient rocks of Colorado show that Snowball Earth really happened
• 3 Diagnostic dilemma: A man's brain started bleeding after a dentist appointment
• 4 Global carbon emissions reach new record high in 2024, with no end in sight, scientists say
• 5 Canada reports 1st local case of H5 bird flu

10 mind-boggling things you should know about quantum physics

From the multiverse to black holes, here’s your cheat sheet to the spooky side of the universe.

1. The quantum world is lumpy

The quantum world has a lot in common with shoes. You can’t just go to a shop and pick out sneakers that are an exact match for your feet. Instead, you’re forced to choose between pairs that come in predetermined sizes.

The subatomic world is similar. Albert Einstein won a Nobel Prize for proving that energy is quantized. Just as you can only buy shoes in multiples of half a size, so energy only comes in multiples of the same "quanta" — hence the name quantum physics.

The quanta here is the Planck constant , named after Max Planck, the godfather of quantum physics. He was trying to solve a problem with our understanding of hot objects like the sun. Our best theories couldn’t match the observations of the energy they kick out. By proposing that energy is quantized, he was able to bring theory neatly into line with experiment.

2. Something can be both wave and particle

J. J. Thomson won the Nobel Prize in 1906 for his discovery that electrons are particles. Yet his son George won the Nobel Prize in 1937 for showing that electrons are waves. Who was right? The answer is both of them. This so-called wave-particle duality is a cornerstone of quantum physics. It applies to light as well as electrons. Sometimes it pays to think about light as an electromagnetic wave, but at other times it’s more useful to picture it in the form of particles called photons. 

• Stephen Hawking: Everything you need to know about the thesis that 'broke the Internet'
• The hunt for wormholes: How scientists look for space-time tunnels

A telescope can focus light waves from distant stars, and also acts as a giant light bucket for collecting photons. It also means that light can exert pressure as photons slam into an object. This is something we already use to propel spacecraft with solar sails, and it may be possible to exploit it in order to maneuver a dangerous asteroid off a collision course with Earth , according to Rusty Schweickart, chairman of the B612 Foundation.

3. Objects can be in two places at once

Wave-particle duality is an example of superposition . That is, a quantum object existing in multiple states at once. An electron, for example, is both ‘here’ and ‘there’ simultaneously. It’s only once we do an experiment to find out where it is that it settles down into one or the other. 

This makes quantum physics all about probabilities. We can only say which state an object is most likely to be in once we look. These odds are encapsulated into a mathematical entity called the wave function. Making an observation is said to ‘collapse’ the wave function, destroying the superposition and forcing the object into just one of its many possible states.

This idea is behind the famous Schrödinger’s cat thought experiment. A cat in a sealed box has its fate linked to a quantum device. As the device exists in both states until a measurement is made, the cat is simultaneously alive and dead until we look.

4. It may lead us towards a multiverse

The idea that observation collapses the wave function and forces a quantum ‘choice’ is known as the Copenhagen interpretation of quantum physics. However, it’s not the only option on the table. Advocates of the ‘many worlds’ interpretation argue that there is no choice involved at all. Instead, at the moment the measurement is made, reality fractures into two copies of itself: one in which we experience outcome A, and another where we see outcome B unfold. It gets around the thorny issue of needing an observer to make stuff happen — does a dog count as an observer, or a robot?

Instead, as far as a quantum particle is concerned, there’s just one very weird reality consisting of many tangled-up layers. As we zoom out towards the larger scales that we experience day to day, those layers untangle into the worlds of the many worlds theory. Physicists call this process decoherence.

5. It helps us characterize stars

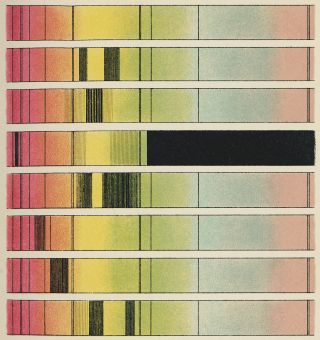
Danish physicist Niels Bohr showed us that the orbits of electrons inside atoms are also quantized. They come in predetermined sizes called energy levels. When an electron drops from a higher energy level to a lower energy level, it spits out a photon with an energy equal to the size of the gap. Equally, an electron can absorb a particle of light and use its energy to leap up to a higher energy level.

Astronomers use this effect all the time. We know what stars are made of because when we break up their light into a rainbow-like spectrum, we see colors that are missing. Different chemical elements have different energy level spacings, so we can work out the constituents of the sun and other stars from the precise colors that are absent.

6. Without it the sun wouldn’t shine

The sun makes its energy through a process called nuclear fusion. It involves two protons — the positively charged particles in an atom — sticking together. However, their identical charges make them repel each other, just like two north poles of a magnet. Physicists call this the Coulomb barrier, and it’s like a wall between the two protons. 

Think of protons as particles and they just collide with the wall and move apart: No fusion, no sunlight. Yet think of them as waves, and it’s a different story. When the wave’s crest reaches the wall, the leading edge has already made it through. The wave’s height represents where the proton is most likely to be. So although it is unlikely to be where the leading edge is, it is there sometimes. It’s as if the proton has burrowed through the barrier, and fusion occurs. Physicists call this effect "quantum tunneling".

7. It stops dead stars collapsing

Eventually fusion in the sun will stop and our star will die. Gravity will win and the sun will collapse, but not indefinitely. The smaller it gets, the more material is crammed together. Eventually a rule of quantum physics called the Pauli exclusion principle comes into play. This says that it is forbidden for certain kinds of particles — such as electrons — to exist in the same quantum state. As gravity tries to do just that, it encounters a resistance that astronomers call degeneracy pressure. The collapse stops, and a new Earth-sized object called a white dwarf forms. 

Degeneracy pressure can only put up so much resistance, however. If a white dwarf grows and approaches a mass equal to 1.4 suns, it triggers a wave of fusion that blasts it to bits. Astronomers call this explosion a Type Ia supernova , and it’s bright enough to outshine an entire galaxy.

8. It causes black holes to evaporate

A quantum rule called the Heisenberg uncertainty principle says that it’s impossible to perfectly know two properties of a system simultaneously. The more accurately you know one, the less precisely you know the other. This applies to momentum and position, and separately to energy and time.

It’s a bit like taking out a loan. You can borrow a lot of money for a short amount of time, or a little cash for longer. This leads us to virtual particles. If enough energy is ‘borrowed’ from nature then a pair of particles can fleetingly pop into existence, before rapidly disappearing so as not to default on the loan.

Stephen Hawking imagined this process occurring at the boundary of a black hole, where one particle escapes (as Hawking radiation), but the other is swallowed. Over time the black hole slowly evaporates, as it’s not paying back the full amount it has borrowed. 

9. It explains the universe’s large-scale structure

Our best theory of the universe’s origin is the Big Bang . Yet it was modified in the 1980s to include another theory called inflation . In the first trillionth of a trillionth of a trillionth of a second, the cosmos ballooned from smaller than an atom to about the size of a grapefruit. That’s a whopping 10^78 times bigger. Inflating a red blood cell by the same amount would make it larger than the entire observable universe today.

As it was initially smaller than an atom, the infant universe would have been dominated by quantum fluctuations linked to the Heisenberg uncertainty principle. Inflation caused the universe to grow rapidly before these fluctuations had a chance to fade away. This concentrated energy into some areas rather than others — something astronomers believe acted as seeds around which material could gather to form the clusters of galaxies we observe now.

10. It is more than a little ‘spooky’

As well as helping to prove that light is quantum, Einstein argued in favor of another effect that he dubbed ‘spooky action at distance’. Today we know that this ‘quantum entanglement’ is real, but we still don’t fully understand what’s going on. Let’s say that we bring two particles together in such a way that their quantum states are inexorably bound, or entangled. One is in state A, and the other in state B.

The Pauli exclusion principle says that they can’t both be in the same state. If we change one, the other instantly changes to compensate. This happens even if we separate the two particles from each other on opposite sides of the universe. It’s as if information about the change we’ve made has traveled between them faster than the speed of light, something Einstein said was impossible.

Join our Space Forums  to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at:  [email protected].

Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: [email protected].

Get the Space.com Newsletter

Breaking space news, the latest updates on rocket launches, skywatching events and more!

Colin Stuart is an award-winning astronomy author, speaker and tutor based in the UK. His popular science books have sold over 400,000 copies worldwide and have been translated into 21 languages. The asteroid (15347) Colinstuart is named after him and he runs an online Astrophysics for Beginners course and a science writing course .

Galaxies get tangled up in 'the queen's hair' in new Hubble Telescope image

Black holes that form in 'reverse Big Bang replays' could account for dark energy

'Snowball Earth:' Entire planet was likely covered in ice more than 600 million years ago

Most Popular

• 2 NASA dealing with aging ISS and spacewalk hardware: 'None of our spacesuits are spring chickens'
• 3 Trump appoints SpaceX's Elon Musk to help head regulation-slashing 'Department of Government Efficiency'
• 4 NASA's Jet Propulsion Lab laying off 5% of its workforce
• 5 'I weigh the same': NASA astronaut Suni Williams refutes tabloid health claims (video)

LOADING PAGE...

Dear Reader,

There are several reasons you might be seeing this page. In order to read the online edition of The Feynman Lectures on Physics , javascript must be supported by your browser and enabled. If you have have visited this website previously it's possible you may have a mixture of incompatible files (.js, .css, and .html) in your browser cache. If you use an ad blocker it may be preventing our pages from downloading necessary resources. So, please try the following: make sure javascript is enabled, clear your browser cache (at least of files from feynmanlectures.caltech.edu), turn off your browser extensions, and open this page:

If it does not open, or only shows you this message again, then please let us know:

• which browser you are using (including version #)
• which operating system you are using (including version #)

This type of problem is rare, and there's a good chance it can be fixed if we have some clues about the cause. So, if you can, after enabling javascript, clearing the cache and disabling extensions, please open your browser's javascript console, load the page above, and if this generates any messages (particularly errors or warnings) on the console, then please make a copy (text or screenshot) of those messages and send them with the above-listed information to the email address given below.

By sending us information you will be helping not only yourself, but others who may be having similar problems accessing the online edition of The Feynman Lectures on Physics . Your time and consideration are greatly appreciated.

Best regards, Mike Gottlieb [email protected] Editor, The Feynman Lectures on Physics New Millennium Edition

1 Quantum Behavior

1–1 Atomic mechanics

“Quantum mechanics” is the description of the behavior of matter and light in all its details and, in particular, of the happenings on an atomic scale. Things on a very small scale behave like nothing that you have any direct experience about. They do not behave like waves, they do not behave like particles, they do not behave like clouds, or billiard balls, or weights on springs, or like anything that you have ever seen.

Newton thought that light was made up of particles, but then it was discovered that it behaves like a wave. Later, however (in the beginning of the twentieth century), it was found that light did indeed sometimes behave like a particle. Historically, the electron, for example, was thought to behave like a particle, and then it was found that in many respects it behaved like a wave. So it really behaves like neither. Now we have given up. We say: “It is like neither .”

There is one lucky break, however—electrons behave just like light. The quantum behavior of atomic objects (electrons, protons, neutrons, photons, and so on) is the same for all, they are all “particle waves,” or whatever you want to call them. So what we learn about the properties of electrons (which we shall use for our examples) will apply also to all “particles,” including photons of light.

The gradual accumulation of information about atomic and small-scale behavior during the first quarter of the 20th century, which gave some indications about how small things do behave, produced an increasing confusion which was finally resolved in 1926 and 1927 by Schrödinger, Heisenberg, and Born. They finally obtained a consistent description of the behavior of matter on a small scale. We take up the main features of that description in this chapter.

Because atomic behavior is so unlike ordinary experience, it is very difficult to get used to, and it appears peculiar and mysterious to everyone—both to the novice and to the experienced physicist. Even the experts do not understand it the way they would like to, and it is perfectly reasonable that they should not, because all of direct, human experience and of human intuition applies to large objects. We know how large objects will act, but things on a small scale just do not act that way. So we have to learn about them in a sort of abstract or imaginative fashion and not by connection with our direct experience.

In this chapter we shall tackle immediately the basic element of the mysterious behavior in its most strange form. We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by “explaining” how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics.

1–2 An experiment with bullets

To try to understand the quantum behavior of electrons, we shall compare and contrast their behavior, in a particular experimental setup, with the more familiar behavior of particles like bullets, and with the behavior of waves like water waves. We consider first the behavior of bullets in the experimental setup shown diagrammatically in Fig.  1–1 . We have a machine gun that shoots a stream of bullets. It is not a very good gun, in that it sprays the bullets (randomly) over a fairly large angular spread, as indicated in the figure. In front of the gun we have a wall (made of armor plate) that has in it two holes just about big enough to let a bullet through. Beyond the wall is a backstop (say a thick wall of wood) which will “absorb” the bullets when they hit it. In front of the backstop we have an object which we shall call a “detector” of bullets. It might be a box containing sand. Any bullet that enters the detector will be stopped and accumulated. When we wish, we can empty the box and count the number of bullets that have been caught. The detector can be moved back and forth (in what we will call the $x$-direction). With this apparatus, we can find out experimentally the answer to the question: “What is the probability that a bullet which passes through the holes in the wall will arrive at the backstop at the distance $x$ from the center?” First, you should realize that we should talk about probability, because we cannot say definitely where any particular bullet will go. A bullet which happens to hit one of the holes may bounce off the edges of the hole, and may end up anywhere at all. By “probability” we mean the chance that the bullet will arrive at the detector, which we can measure by counting the number which arrive at the detector in a certain time and then taking the ratio of this number to the total number that hit the backstop during that time. Or, if we assume that the gun always shoots at the same rate during the measurements, the probability we want is just proportional to the number that reach the detector in some standard time interval.

For our present purposes we would like to imagine a somewhat idealized experiment in which the bullets are not real bullets, but are indestructible bullets—they cannot break in half. In our experiment we find that bullets always arrive in lumps, and when we find something in the detector, it is always one whole bullet. If the rate at which the machine gun fires is made very low, we find that at any given moment either nothing arrives, or one and only one—exactly one—bullet arrives at the backstop. Also, the size of the lump certainly does not depend on the rate of firing of the gun. We shall say: “Bullets always arrive in identical lumps.” What we measure with our detector is the probability of arrival of a lump. And we measure the probability as a function of $x$. The result of such measurements with this apparatus (we have not yet done the experiment, so we are really imagining the result) are plotted in the graph drawn in part (c) of Fig.  1–1 . In the graph we plot the probability to the right and $x$ vertically, so that the $x$-scale fits the diagram of the apparatus. We call the probability $P_{12}$ because the bullets may have come either through hole $1$ or through hole $2$. You will not be surprised that $P_{12}$ is large near the middle of the graph but gets small if $x$ is very large. You may wonder, however, why $P_{12}$ has its maximum value at $x=0$. We can understand this fact if we do our experiment again after covering up hole $2$, and once more while covering up hole $1$. When hole $2$ is covered, bullets can pass only through hole $1$, and we get the curve marked $P_1$ in part (b) of the figure. As you would expect, the maximum of $P_1$ occurs at the value of $x$ which is on a straight line with the gun and hole $1$. When hole $1$ is closed, we get the symmetric curve $P_2$ drawn in the figure. $P_2$ is the probability distribution for bullets that pass through hole $2$. Comparing parts (b) and (c) of Fig.  1–1 , we find the important result that \begin{equation} \label{Eq:III:1:1} P_{12}=P_1+P_2. \end{equation} The probabilities just add together. The effect with both holes open is the sum of the effects with each hole open alone. We shall call this result an observation of “ no interference ,” for a reason that you will see later. So much for bullets. They come in lumps, and their probability of arrival shows no interference.

1–3 An experiment with waves

Now we wish to consider an experiment with water waves. The apparatus is shown diagrammatically in Fig.  1–2 . We have a shallow trough of water. A small object labeled the “wave source” is jiggled up and down by a motor and makes circular waves. To the right of the source we have again a wall with two holes, and beyond that is a second wall, which, to keep things simple, is an “absorber,” so that there is no reflection of the waves that arrive there. This can be done by building a gradual sand “beach.” In front of the beach we place a detector which can be moved back and forth in the $x$-direction, as before. The detector is now a device which measures the “intensity” of the wave motion. You can imagine a gadget which measures the height of the wave motion, but whose scale is calibrated in proportion to the square of the actual height, so that the reading is proportional to the intensity of the wave. Our detector reads, then, in proportion to the energy being carried by the wave—or rather, the rate at which energy is carried to the detector.

With our wave apparatus, the first thing to notice is that the intensity can have any size. If the source just moves a very small amount, then there is just a little bit of wave motion at the detector. When there is more motion at the source, there is more intensity at the detector. The intensity of the wave can have any value at all. We would not say that there was any “lumpiness” in the wave intensity.

Now let us measure the wave intensity for various values of $x$ (keeping the wave source operating always in the same way). We get the interesting-looking curve marked $I_{12}$ in part (c) of the figure.

We have already worked out how such patterns can come about when we studied the interference of electric waves in Volume I. In this case we would observe that the original wave is diffracted at the holes, and new circular waves spread out from each hole. If we cover one hole at a time and measure the intensity distribution at the absorber we find the rather simple intensity curves shown in part (b) of the figure. $I_1$ is the intensity of the wave from hole $1$ (which we find by measuring when hole $2$ is blocked off) and $I_2$ is the intensity of the wave from hole $2$ (seen when hole $1$ is blocked).

The intensity $I_{12}$ observed when both holes are open is certainly not the sum of $I_1$ and $I_2$. We say that there is “interference” of the two waves. At some places (where the curve $I_{12}$ has its maxima) the waves are “in phase” and the wave peaks add together to give a large amplitude and, therefore, a large intensity. We say that the two waves are “interfering constructively” at such places. There will be such constructive interference wherever the distance from the detector to one hole is a whole number of wavelengths larger (or shorter) than the distance from the detector to the other hole.

At those places where the two waves arrive at the detector with a phase difference of $\pi$ (where they are “out of phase”) the resulting wave motion at the detector will be the difference of the two amplitudes. The waves “interfere destructively,” and we get a low value for the wave intensity. We expect such low values wherever the distance between hole $1$ and the detector is different from the distance between hole $2$ and the detector by an odd number of half-wavelengths. The low values of $I_{12}$ in Fig.  1–2 correspond to the places where the two waves interfere destructively.

You will remember that the quantitative relationship between $I_1$, $I_2$, and $I_{12}$ can be expressed in the following way: The instantaneous height of the water wave at the detector for the wave from hole $1$ can be written as (the real part of) $h_1e^{i\omega t}$, where the “amplitude” $h_1$ is, in general, a complex number. The intensity is proportional to the mean squared height or, when we use the complex numbers, to the absolute value squared $\abs{h_1}^2$. Similarly, for hole $2$ the height is $h_2e^{i\omega t}$ and the intensity is proportional to $\abs{h_2}^2$. When both holes are open, the wave heights add to give the height $(h_1+h_2)e^{i\omega t}$ and the intensity $\abs{h_1+h_2}^2$. Omitting the constant of proportionality for our present purposes, the proper relations for interfering waves are \begin{equation} \label{Eq:III:1:2} I_1=\abs{h_1}^2,\quad I_2=\abs{h_2}^2,\quad I_{12}=\abs{h_1+h_2}^2. \end{equation}

You will notice that the result is quite different from that obtained with bullets (Eq.  1.1 ). If we expand $\abs{h_1+h_2}^2$ we see that \begin{equation} \label{Eq:III:1:3} \abs{h_1+h_2}^2=\abs{h_1}^2+\abs{h_2}^2+2\abs{h_1}\abs{h_2}\cos\delta, \end{equation} where $\delta$ is the phase difference between $h_1$ and $h_2$. In terms of the intensities, we could write \begin{equation} \label{Eq:III:1:4} I_{12}=I_1+I_2+2\sqrt{I_1I_2}\cos\delta. \end{equation} The last term in ( 1.4 ) is the “interference term.” So much for water waves. The intensity can have any value, and it shows interference.

1–4 An experiment with electrons

Now we imagine a similar experiment with electrons. It is shown diagrammatically in Fig.  1–3 . We make an electron gun which consists of a tungsten wire heated by an electric current and surrounded by a metal box with a hole in it. If the wire is at a negative voltage with respect to the box, electrons emitted by the wire will be accelerated toward the walls and some will pass through the hole. All the electrons which come out of the gun will have (nearly) the same energy. In front of the gun is again a wall (just a thin metal plate) with two holes in it. Beyond the wall is another plate which will serve as a “backstop.” In front of the backstop we place a movable detector. The detector might be a geiger counter or, perhaps better, an electron multiplier, which is connected to a loudspeaker.

We should say right away that you should not try to set up this experiment (as you could have done with the two we have already described). This experiment has never been done in just this way. The trouble is that the apparatus would have to be made on an impossibly small scale to show the effects we are interested in. We are doing a “thought experiment,” which we have chosen because it is easy to think about. We know the results that would be obtained because there are many experiments that have been done, in which the scale and the proportions have been chosen to show the effects we shall describe.

The first thing we notice with our electron experiment is that we hear sharp “clicks” from the detector (that is, from the loudspeaker). And all “clicks” are the same. There are no “half-clicks.”

We would also notice that the “clicks” come very erratically. Something like: click ….. click-click … click …….. click …. click-click …… click …, etc., just as you have, no doubt, heard a geiger counter operating. If we count the clicks which arrive in a sufficiently long time—say for many minutes—and then count again for another equal period, we find that the two numbers are very nearly the same. So we can speak of the average rate at which the clicks are heard (so-and-so-many clicks per minute on the average).

As we move the detector around, the rate at which the clicks appear is faster or slower, but the size (loudness) of each click is always the same. If we lower the temperature of the wire in the gun, the rate of clicking slows down, but still each click sounds the same. We would notice also that if we put two separate detectors at the backstop, one or the other would click, but never both at once. (Except that once in a while, if there were two clicks very close together in time, our ear might not sense the separation.) We conclude, therefore, that whatever arrives at the backstop arrives in “lumps.” All the “lumps” are the same size: only whole “lumps” arrive, and they arrive one at a time at the backstop. We shall say: “Electrons always arrive in identical lumps.”

Just as for our experiment with bullets, we can now proceed to find experimentally the answer to the question: “What is the relative probability that an electron ‘lump’ will arrive at the backstop at various distances $x$ from the center?” As before, we obtain the relative probability by observing the rate of clicks, holding the operation of the gun constant. The probability that lumps will arrive at a particular $x$ is proportional to the average rate of clicks at that $x$.

The result of our experiment is the interesting curve marked $P_{12}$ in part (c) of Fig.  1–3 . Yes! That is the way electrons go.

1–5 The interference of electron waves

Now let us try to analyze the curve of Fig.  1–3 to see whether we can understand the behavior of the electrons. The first thing we would say is that since they come in lumps, each lump, which we may as well call an electron, has come either through hole $1$ or through hole $2$. Let us write this in the form of a “Proposition”:

Proposition A: Each electron either goes through hole $1$ or it goes through hole $2$.

Assuming Proposition A, all electrons that arrive at the backstop can be divided into two classes: (1) those that come through hole $1$, and (2) those that come through hole $2$. So our observed curve must be the sum of the effects of the electrons which come through hole $1$ and the electrons which come through hole $2$. Let us check this idea by experiment. First, we will make a measurement for those electrons that come through hole $1$. We block off hole $2$ and make our counts of the clicks from the detector. From the clicking rate, we get $P_1$. The result of the measurement is shown by the curve marked $P_1$ in part (b) of Fig.  1–3 . The result seems quite reasonable. In a similar way, we measure $P_2$, the probability distribution for the electrons that come through hole $2$. The result of this measurement is also drawn in the figure.

The result $P_{12}$ obtained with both holes open is clearly not the sum of $P_1$ and $P_2$, the probabilities for each hole alone. In analogy with our water-wave experiment, we say: “There is interference.” \begin{equation} \label{Eq:III:1:5} \text{For electrons:}\quad P_{12}\neq P_1+P_2. \end{equation}

How can such an interference come about? Perhaps we should say: “Well, that means, presumably, that it is not true that the lumps go either through hole $1$ or hole $2$, because if they did, the probabilities should add. Perhaps they go in a more complicated way. They split in half and …” But no! They cannot, they always arrive in lumps … “Well, perhaps some of them go through $1$, and then they go around through $2$, and then around a few more times, or by some other complicated path … then by closing hole $2$, we changed the chance that an electron that started out through hole $1$ would finally get to the backstop …” But notice! There are some points at which very few electrons arrive when both holes are open, but which receive many electrons if we close one hole, so closing one hole increased the number from the other. Notice, however, that at the center of the pattern, $P_{12}$ is more than twice as large as $P_1+P_2$. It is as though closing one hole decreased the number of electrons which come through the other hole. It seems hard to explain both effects by proposing that the electrons travel in complicated paths.

It is all quite mysterious. And the more you look at it the more mysterious it seems. Many ideas have been concocted to try to explain the curve for $P_{12}$ in terms of individual electrons going around in complicated ways through the holes. None of them has succeeded. None of them can get the right curve for $P_{12}$ in terms of $P_1$ and $P_2$.

Yet, surprisingly enough, the mathematics for relating $P_1$ and $P_2$ to $P_{12}$ is extremely simple. For $P_{12}$ is just like the curve $I_{12}$ of Fig.  1–2 , and that was simple. What is going on at the backstop can be described by two complex numbers that we can call $\phi_1$ and $\phi_2$ (they are functions of $x$, of course). The absolute square of $\phi_1$ gives the effect with only hole $1$ open. That is, $P_1=\abs{\phi_1}^2$. The effect with only hole $2$ open is given by $\phi_2$ in the same way. That is, $P_2=\abs{\phi_2}^2$. And the combined effect of the two holes is just $P_{12}=\abs{\phi_1+\phi_2}^2$. The mathematics is the same as that we had for the water waves! (It is hard to see how one could get such a simple result from a complicated game of electrons going back and forth through the plate on some strange trajectory.)

We conclude the following: The electrons arrive in lumps, like particles, and the probability of arrival of these lumps is distributed like the distribution of intensity of a wave. It is in this sense that an electron behaves “sometimes like a particle and sometimes like a wave.”

Incidentally, when we were dealing with classical waves we defined the intensity as the mean over time of the square of the wave amplitude, and we used complex numbers as a mathematical trick to simplify the analysis. But in quantum mechanics it turns out that the amplitudes must be represented by complex numbers. The real parts alone will not do. That is a technical point, for the moment, because the formulas look just the same.

Since the probability of arrival through both holes is given so simply, although it is not equal to $(P_1+P_2)$, that is really all there is to say. But there are a large number of subtleties involved in the fact that nature does work this way. We would like to illustrate some of these subtleties for you now. First, since the number that arrives at a particular point is not equal to the number that arrives through $1$ plus the number that arrives through $2$, as we would have concluded from Proposition A, undoubtedly we should conclude that Proposition A is false . It is not true that the electrons go either through hole $1$ or hole $2$. But that conclusion can be tested by another experiment.

1–6 Watching the electrons

We shall now try the following experiment. To our electron apparatus we add a very strong light source, placed behind the wall and between the two holes, as shown in Fig.  1–4 . We know that electric charges scatter light. So when an electron passes, however it does pass, on its way to the detector, it will scatter some light to our eye, and we can see where the electron goes. If, for instance, an electron were to take the path via hole $2$ that is sketched in Fig.  1–4 , we should see a flash of light coming from the vicinity of the place marked $A$ in the figure. If an electron passes through hole $1$, we would expect to see a flash from the vicinity of the upper hole. If it should happen that we get light from both places at the same time, because the electron divides in half … Let us just do the experiment!

Here is what we see: every time that we hear a “click” from our electron detector (at the backstop), we also see a flash of light either near hole $1$ or near hole $2$, but never both at once! And we observe the same result no matter where we put the detector. From this observation we conclude that when we look at the electrons we find that the electrons go either through one hole or the other. Experimentally, Proposition A is necessarily true.

What, then, is wrong with our argument against Proposition A? Why isn’t  $P_{12}$ just equal to $P_1+P_2$? Back to experiment! Let us keep track of the electrons and find out what they are doing. For each position ($x$-location) of the detector we will count the electrons that arrive and also keep track of which hole they went through, by watching for the flashes. We can keep track of things this way: whenever we hear a “click” we will put a count in Column $1$ if we see the flash near hole $1$, and if we see the flash near hole $2$, we will record a count in Column $2$. Every electron which arrives is recorded in one of two classes: those which come through $1$ and those which come through $2$. From the number recorded in Column $1$ we get the probability $P_1'$ that an electron will arrive at the detector via hole $1$; and from the number recorded in Column $2$ we get $P_2'$, the probability that an electron will arrive at the detector via hole $2$. If we now repeat such a measurement for many values of $x$, we get the curves for $P_1'$ and $P_2'$ shown in part (b) of Fig.  1–4 .

Well, that is not too surprising! We get for $P_1'$ something quite similar to what we got before for $P_1$ by blocking off hole $2$; and $P_2'$ is similar to what we got by blocking hole $1$. So there is not any complicated business like going through both holes. When we watch them, the electrons come through just as we would expect them to come through. Whether the holes are closed or open, those which we see come through hole $1$ are distributed in the same way whether hole $2$ is open or closed.

But wait! What do we have now for the total probability, the probability that an electron will arrive at the detector by any route? We already have that information. We just pretend that we never looked at the light flashes, and we lump together the detector clicks which we have separated into the two columns. We must just add the numbers. For the probability that an electron will arrive at the backstop by passing through either hole, we do find $P_{12}'=P_1'+P_2'$. That is, although we succeeded in watching which hole our electrons come through, we no longer get the old interference curve $P_{12}$, but a new one, $P_{12}'$, showing no interference! If we turn out the light $P_{12}$ is restored.

We must conclude that when we look at the electrons the distribution of them on the screen is different than when we do not look. Perhaps it is turning on our light source that disturbs things? It must be that the electrons are very delicate, and the light, when it scatters off the electrons, gives them a jolt that changes their motion. We know that the electric field of the light acting on a charge will exert a force on it. So perhaps we should expect the motion to be changed. Anyway, the light exerts a big influence on the electrons. By trying to “watch” the electrons we have changed their motions. That is, the jolt given to the electron when the photon is scattered by it is such as to change the electron’s motion enough so that if it might have gone to where $P_{12}$ was at a maximum it will instead land where $P_{12}$ was a minimum; that is why we no longer see the wavy interference effects.

You may be thinking: “Don’t use such a bright source! Turn the brightness down! The light waves will then be weaker and will not disturb the electrons so much. Surely, by making the light dimmer and dimmer, eventually the wave will be weak enough that it will have a negligible effect.” O.K. Let’s try it. The first thing we observe is that the flashes of light scattered from the electrons as they pass by does not get weaker. It is always the same-sized flash . The only thing that happens as the light is made dimmer is that sometimes we hear a “click” from the detector but see no flash at all . The electron has gone by without being “seen.” What we are observing is that light also acts like electrons, we knew that it was “wavy,” but now we find that it is also “lumpy.” It always arrives—or is scattered—in lumps that we call “photons.” As we turn down the intensity of the light source we do not change the size of the photons, only the rate at which they are emitted. That explains why, when our source is dim, some electrons get by without being seen. There did not happen to be a photon around at the time the electron went through.

This is all a little discouraging. If it is true that whenever we “see” the electron we see the same-sized flash, then those electrons we see are always the disturbed ones. Let us try the experiment with a dim light anyway. Now whenever we hear a click in the detector we will keep a count in three columns: in Column (1) those electrons seen by hole $1$, in Column (2) those electrons seen by hole $2$, and in Column (3) those electrons not seen at all. When we work up our data (computing the probabilities) we find these results: Those “seen by hole $1$” have a distribution like $P_1'$; those “seen by hole $2$” have a distribution like $P_2'$ (so that those “seen by either hole $1$ or $2$” have a distribution like $P_{12}'$); and those “not seen at all” have a “wavy” distribution just like $P_{12}$ of Fig.  1–3 ! If the electrons are not seen, we have interference!

That is understandable. When we do not see the electron, no photon disturbs it, and when we do see it, a photon has disturbed it. There is always the same amount of disturbance because the light photons all produce the same-sized effects and the effect of the photons being scattered is enough to smear out any interference effect.

Is there not some way we can see the electrons without disturbing them? We learned in an earlier chapter that the momentum carried by a “photon” is inversely proportional to its wavelength ($p=h/\lambda$). Certainly the jolt given to the electron when the photon is scattered toward our eye depends on the momentum that photon carries. Aha! If we want to disturb the electrons only slightly we should not have lowered the intensity of the light, we should have lowered its frequency (the same as increasing its wavelength). Let us use light of a redder color. We could even use infrared light, or radiowaves (like radar), and “see” where the electron went with the help of some equipment that can “see” light of these longer wavelengths. If we use “gentler” light perhaps we can avoid disturbing the electrons so much.

Let us try the experiment with longer waves. We shall keep repeating our experiment, each time with light of a longer wavelength. At first, nothing seems to change. The results are the same. Then a terrible thing happens. You remember that when we discussed the microscope we pointed out that, due to the wave nature of the light, there is a limitation on how close two spots can be and still be seen as two separate spots. This distance is of the order of the wavelength of light. So now, when we make the wavelength longer than the distance between our holes, we see a big fuzzy flash when the light is scattered by the electrons. We can no longer tell which hole the electron went through! We just know it went somewhere! And it is just with light of this color that we find that the jolts given to the electron are small enough so that $P_{12}'$ begins to look like $P_{12}$—that we begin to get some interference effect. And it is only for wavelengths much longer than the separation of the two holes (when we have no chance at all of telling where the electron went) that the disturbance due to the light gets sufficiently small that we again get the curve $P_{12}$ shown in Fig.  1–3 .

In our experiment we find that it is impossible to arrange the light in such a way that one can tell which hole the electron went through, and at the same time not disturb the pattern. It was suggested by Heisenberg that the then new laws of nature could only be consistent if there were some basic limitation on our experimental capabilities not previously recognized. He proposed, as a general principle, his uncertainty principle , which we can state in terms of our experiment as follows: “It is impossible to design an apparatus to determine which hole the electron passes through, that will not at the same time disturb the electrons enough to destroy the interference pattern.” If an apparatus is capable of determining which hole the electron goes through, it cannot be so delicate that it does not disturb the pattern in an essential way. No one has ever found (or even thought of) a way around the uncertainty principle. So we must assume that it describes a basic characteristic of nature.

The complete theory of quantum mechanics which we now use to describe atoms and, in fact, all matter, depends on the correctness of the uncertainty principle. Since quantum mechanics is such a successful theory, our belief in the uncertainty principle is reinforced. But if a way to “beat” the uncertainty principle were ever discovered, quantum mechanics would give inconsistent results and would have to be discarded as a valid theory of nature.

“Well,” you say, “what about Proposition A? Is it true, or is it not true, that the electron either goes through hole $1$ or it goes through hole $2$?” The only answer that can be given is that we have found from experiment that there is a certain special way that we have to think in order that we do not get into inconsistencies. What we must say (to avoid making wrong predictions) is the following. If one looks at the holes or, more accurately, if one has a piece of apparatus which is capable of determining whether the electrons go through hole $1$ or hole $2$, then one can say that it goes either through hole $1$ or hole $2$. But , when one does not try to tell which way the electron goes, when there is nothing in the experiment to disturb the electrons, then one may not say that an electron goes either through hole $1$ or hole $2$. If one does say that, and starts to make any deductions from the statement, he will make errors in the analysis. This is the logical tightrope on which we must walk if we wish to describe nature successfully.

If the motion of all matter—as well as electrons—must be described in terms of waves, what about the bullets in our first experiment? Why didn’t we see an interference pattern there? It turns out that for the bullets the wavelengths were so tiny that the interference patterns became very fine. So fine, in fact, that with any detector of finite size one could not distinguish the separate maxima and minima. What we saw was only a kind of average, which is the classical curve. In Fig.  1–5 we have tried to indicate schematically what happens with large-scale objects. Part (a) of the figure shows the probability distribution one might predict for bullets, using quantum mechanics. The rapid wiggles are supposed to represent the interference pattern one gets for waves of very short wavelength. Any physical detector, however, straddles several wiggles of the probability curve, so that the measurements show the smooth curve drawn in part (b) of the figure.

1–7 First principles of quantum mechanics

We will now write a summary of the main conclusions of our experiments. We will, however, put the results in a form which makes them true for a general class of such experiments. We can write our summary more simply if we first define an “ideal experiment” as one in which there are no uncertain external influences, i.e., no jiggling or other things going on that we cannot take into account. We would be quite precise if we said: “An ideal experiment is one in which all of the initial and final conditions of the experiment are completely specified.” What we will call “an event” is, in general, just a specific set of initial and final conditions. (For example: “an electron leaves the gun, arrives at the detector, and nothing else happens.”) Now for our summary.

• The probability of an event in an ideal experiment is given by the square of the absolute value of a complex number $\phi$ which is called the probability amplitude: \begin{equation} \begin{aligned} P&=\text{probability},\\ \phi&=\text{probability amplitude},\\ P&=\abs{\phi}^2. \end{aligned} \label{Eq:III:1:6} \end{equation}
• When an event can occur in several alternative ways, the probability amplitude for the event is the sum of the probability amplitudes for each way considered separately. There is interference: \begin{equation} \begin{aligned} \phi&=\phi_1+\phi_2,\\ P&=\abs{\phi_1+\phi_2}^2. \end{aligned} \label{Eq:III:1:7} \end{equation}
• If an experiment is performed which is capable of determining whether one or another alternative is actually taken, the probability of the event is the sum of the probabilities for each alternative. The interference is lost: \begin{equation} \label{Eq:III:1:8} P=P_1+P_2. \end{equation}

One might still like to ask: “How does it work? What is the machinery behind the law?” No one has found any machinery behind the law. No one can “explain” any more than we have just “explained.” No one will give you any deeper representation of the situation. We have no ideas about a more basic mechanism from which these results can be deduced.

We would like to emphasize a very important difference between classical and quantum mechanics . We have been talking about the probability that an electron will arrive in a given circumstance. We have implied that in our experimental arrangement (or even in the best possible one) it would be impossible to predict exactly what would happen. We can only predict the odds! This would mean, if it were true, that physics has given up on the problem of trying to predict exactly what will happen in a definite circumstance. Yes! physics has given up. We do not know how to predict what would happen in a given circumstance , and we believe now that it is impossible—that the only thing that can be predicted is the probability of different events. It must be recognized that this is a retrenchment in our earlier ideal of understanding nature. It may be a backward step, but no one has seen a way to avoid it.

We make now a few remarks on a suggestion that has sometimes been made to try to avoid the description we have given: “Perhaps the electron has some kind of internal works—some inner variables—that we do not yet know about. Perhaps that is why we cannot predict what will happen. If we could look more closely at the electron, we could be able to tell where it would end up.” So far as we know, that is impossible. We would still be in difficulty. Suppose we were to assume that inside the electron there is some kind of machinery that determines where it is going to end up. That machine must also determine which hole it is going to go through on its way. But we must not forget that what is inside the electron should not be dependent on what we do, and in particular upon whether we open or close one of the holes. So if an electron, before it starts, has already made up its mind (a) which hole it is going to use, and (b) where it is going to land, we should find $P_1$ for those electrons that have chosen hole $1$, $P_2$ for those that have chosen hole $2$, and necessarily the sum $P_1+P_2$ for those that arrive through the two holes. There seems to be no way around this. But we have verified experimentally that that is not the case. And no one has figured a way out of this puzzle. So at the present time we must limit ourselves to computing probabilities. We say “at the present time,” but we suspect very strongly that it is something that will be with us forever—that it is impossible to beat that puzzle—that this is the way nature really is .

1–8 The uncertainty principle

This is the way Heisenberg stated the uncertainty principle originally: If you make the measurement on any object, and you can determine the $x$-component of its momentum with an uncertainty $\Delta p$, you cannot, at the same time, know its $x$-position more accurately than $\Delta x\geq\hbar/2\Delta p$, where $\hbar$ is a definite fixed number given by nature. It is called the “reduced Planck constant,” and is approximately $1.05\times10^{-34}$ joule-seconds. The uncertainties in the position and momentum of a particle at any instant must have their product greater than or equal to half the reduced Planck constant. This is a special case of the uncertainty principle that was stated above more generally. The more general statement was that one cannot design equipment in any way to determine which of two alternatives is taken, without, at the same time, destroying the pattern of interference.

Let us show for one particular case that the kind of relation given by Heisenberg must be true in order to keep from getting into trouble. We imagine a modification of the experiment of Fig.  1–3 , in which the wall with the holes consists of a plate mounted on rollers so that it can move freely up and down (in the $x$-direction), as shown in Fig.  1–6 . By watching the motion of the plate carefully we can try to tell which hole an electron goes through. Imagine what happens when the detector is placed at $x=0$. We would expect that an electron which passes through hole $1$ must be deflected downward by the plate to reach the detector. Since the vertical component of the electron momentum is changed, the plate must recoil with an equal momentum in the opposite direction. The plate will get an upward kick. If the electron goes through the lower hole, the plate should feel a downward kick. It is clear that for every position of the detector, the momentum received by the plate will have a different value for a traversal via hole $1$ than for a traversal via hole $2$. So! Without disturbing the electrons at all , but just by watching the plate , we can tell which path the electron used.

Now in order to do this it is necessary to know what the momentum of the screen is, before the electron goes through. So when we measure the momentum after the electron goes by, we can figure out how much the plate’s momentum has changed. But remember, according to the uncertainty principle we cannot at the same time know the position of the plate with an arbitrary accuracy. But if we do not know exactly where the plate is, we cannot say precisely where the two holes are. They will be in a different place for every electron that goes through. This means that the center of our interference pattern will have a different location for each electron. The wiggles of the interference pattern will be smeared out. We shall show quantitatively in the next chapter that if we determine the momentum of the plate sufficiently accurately to determine from the recoil measurement which hole was used, then the uncertainty in the $x$-position of the plate will, according to the uncertainty principle, be enough to shift the pattern observed at the detector up and down in the $x$-direction about the distance from a maximum to its nearest minimum. Such a random shift is just enough to smear out the pattern so that no interference is observed.

The uncertainty principle “protects” quantum mechanics. Heisenberg recognized that if it were possible to measure the momentum and the position simultaneously with a greater accuracy, the quantum mechanics would collapse. So he proposed that it must be impossible. Then people sat down and tried to figure out ways of doing it, and nobody could figure out a way to measure the position and the momentum of anything—a screen, an electron, a billiard ball, anything—with any greater accuracy. Quantum mechanics maintains its perilous but still correct existence.

The Double-Slit Experiment That Blew Open Quantum Mechanics

Is light a wave or a particle? Yes.

The physics equations you learned in school don't work on the atomic scale. We have Newtonian physics to explain the world we can see and feel, and we have Einsteinian physics to explain the behavior of matter and light in the universe, but we observe a bunch of bizarre phenomena on the atomic scale that we can't explain fully yet with equations and mathematical laws.

Perhaps the two most perplexing behaviors of atomic particles are quantum superposition ( particles can exist in two separate places simultaneously ) and quantum entanglement (particles separated by large distances can react to one another instantaneously, suggesting information can travel faster than the speed of light, although there are other explanations for this phenomenon as well).

The experiment that started physicists down the path to discovering the wonderfully spooky behaviors of atomic particles is called the double-slit experiment. We know that light travels in waves, and when those waves pass through two parallel slits, a single wave gets separated into two waves that run into each other. PBS's Space Time series has a great new video explaining the double-slit experiment.

When we shoot two waves of light through a double slit, they form a pattern based on the way their peaks and troughs match up or clash. When we shoot a single photon through, we'd expect it to just go through unchanged. But it won't. When you shoot enough single photons through—one at a time, alternating slits—they form the same interference pattern as the waves of light. Basically, that means that all the possible paths of these particles can interfere with each other, even though only one of the possible paths actually happens. Mind blown?

We can't fully explain these phenomena yet, but we can observe them. (The video above runs through some of the leading theories for these odd quantum behaviors. It's trippy stuff.) It is only a matter of time before someone comes up with the correct mathematical equations to fully predict and model these events, and when they do, the third major set of physical laws will be born.

Jay Bennett is the associate editor of PopularMechanics.com. He has also written for Smithsonian, Popular Science and Outside Magazine. 

Scientists Think Gravity Might Be a Quantum Field

Cloned Black-Footed Ferret Births Two Healthy Kits

Plastered Pompeii Victims’ DNA Corrects Record

A Missing World War II Destroyer Has Been Found

The Head Transplant Doctor Will See You Now

A Secret Climate Weapon Met Scientist’s Wild Goal

Scientists Made Animal Cells Do Photosynthesis

One of These Materials Could Make Fusion Possible

Piecing Together the Building Blocks of Life

Spotting Quantum Tornadoes Inside a Supersolid

King Tut’s Mask Wasn’t Meant for Him

Swiss Alps Ice Reveals Mysterious Bamboo Cart

Open Yale Courses

You are here, phys 201: fundamentals of physics ii,  - quantum mechanics i: key experiments and wave-particle duality.

The double slit experiment, which implies the end of Newtonian Mechanics, is described. The de Broglie relation between wavelength and momentum is deduced from experiment for photons and electrons. The photoelectric effect and Compton scattering, which provided experimental support for Einstein’s photon theory of light, are reviewed. The wave function is introduced along with the probability interpretation. The uncertainty principle is shown to arise from the fact that the particle’s location is determined by a wave and that waves diffract when passing a narrow opening.

Lecture Chapters

• Recap of Young's Double Slit Experiment
• The Particulate Nature of Light
• The Photoelectric Effect
• Compton's Scattering
• Particle-Wave Duality of Matter
• The Uncertainty Principle

share this!

November 13, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

peer-reviewed publication

trusted source

How 'clean' does a quantum computing test facility need to be?

by Karyn Hede, Pacific Northwest National Laboratory

Now is the time to banish low-level radioactive energy sources from facilities that house and conduct experiments with superconducting qubits, according to a pair of recently published studies. Significantly improving quantum device coherence times is a key step toward an era of practical quantum computing.

Two complementary articles, published in the journal PRX Quantum and the Journal of Instrumentation , outline which sources of interfering ionizing radiation are most problematic for superconducting quantum computers and how to address them. The findings set the stage for quantitative study of errors caused by radiation effects in shielded underground facilities.

A research team led by physicists at the Department of Energy's Pacific Northwest National Laboratory, in collaboration with colleagues at MIT's Lincoln Laboratory, the National Institute of Standards and Technology, along with multiple academic partners, published their findings to assist the quantum computing community to prepare for the next generation of qubit development.

Electronic 'noise' undermines efforts to extend qubit life

"The time is coming soon when advances in design and materials will result in qubits stable enough that environmental effects from stray radiation become the rate-limiting step to quantum coherence," said physicist Brent VanDevender, one of the research team leads. VanDevender was one of the first scientists to identify natural ionizing radiation as a source of instability for the functioning of qubits, the basic unit of a quantum computer.

Even the slightest interference can cause errors that lead superconducting qubits to lose their quantum state, a process known as decoherence. The research team found that cosmic radiation and naturally occurring isotopes, which emit low levels of ionizing radiation and are found in common materials, are about equally responsible for causing decoherence.

"Once we established the effect of ionizing radiation on superconducting qubits, we knew we needed to systematically and quantitatively identify sources of radiation in the environment," said lead experimental physicist Ben Loer.

"Our experience with measuring ultra-low levels of radiation in the laboratory led us to include radiation sources within the very experimental units, cryostats, where these experimental qubits are studied."

"We found that a lot of the electrical connectors are just filthy dirty from the standpoint of acting as a radiation source," VanDevender added.

Cleaning up underground

Combined, the two studies point to effective measures for shielding sensitive experimental equipment from the effects of radiation exposure.

In the article in the Journal of Instrumentation , the research team describes the precautions taken to greatly reduce the potential for atmospheric and isotope radiation exposure in a shielded underground qubit testbed facility on the Richland, Washington campus of PNNL called the Low Background Cryogenic Facility.

Constructed within an existing ultra-clean underground laboratory, the test bed includes a cryostat, also known as a dilution refrigerator, capable of cooling superconducting qubit devices to near absolute zero, a key to stabilizing quantum computing devices of this design. The research team reports that this lead-shielded cryostat could reduce the error rate by 20 times compared with the error rate seen in a typical above-ground, unshielded facility.

In addition, the team reports that certain relatively simple precautions, such as eliminating natural sources of radiation within materials inside the dilution refrigerator, go a long way toward making quantum computing devices viable. These sources include metal isotopes—naturally occurring variants of elements that spontaneously eject radiation in the form of alpha, beta, and gamma rays—which can interfere with quantum devices.

In their exploration of these radiation sources within the lab, they used specialized ultrasensitive detection methods to identify contaminants in silicon, copper and ceramic electronic components such as circuit boards and cables used to collect data from instruments, and even the qubits themselves.

To reduce the impact from these devices, the team advises using materials like brass instead of beryllium-copper alloys typically found in cables. Future goals of this research include testing the effectiveness of "radiation-hardened" qubits that are less sensitive to the impact of radiation and studying low-background materials.

Transferring knowledge from sensitive detection technology

In the companion study , published in PRX Quantum , the research team directly measured ionizing radiation interactions on a superconducting sensor inside a cryocooler, a refrigerator that can reach ultra-cold cryogenic temperatures. They used simple radiation detection circuits printed on a piece of silicon similar to that used for qubits.

Here they showed that stray radiation that interacts with a silicon circuit board and that could possibly cause decoherence in a qubit or other "unwelcome effects on circuit performance" matches well with the predicted rate and energy spectrum.

The research team relied on expertise developed during design and building of double beta decay detectors, neutrino detectors and dark matter detectors, which are similarly sensitive to low levels of radiation. They identified two complementary approaches to reducing the sensitivity of superconducting elements to stray radiation as first steps toward "radiation hardening:" isolating the superconducting elements on crystal "islands" and simply making the crystal substrate thinner.

"We've demonstrated which sources of radiation are important, and we're eager to see how new devices will perform in our low-background facility," said Loer.

B. Loer et al, Abatement of ionizing radiation for superconducting quantum devices, Journal of Instrumentation (2024). DOI: 10.1088/1748-0221/19/09/P09001

Journal information: PRX Quantum

Provided by Pacific Northwest National Laboratory

Explore further

Feedback to editors

Meteorite contains evidence of liquid water on Mars 742 million years ago

3 hours ago

Ocean warming and acidification threaten key ocean plankton groups, study warns

4 hours ago

Metagenomic profiling method with enhanced precision uses fewer computing resources

Scientists identify flaw in astrophysics models of massive stars and supernovae

Colorado River basins could face tipping point, drought study warns

5 hours ago

CMS develops new AI algorithm to detect anomalies at the Large Hadron Collider

Swift Observatory studies a pair of gas-churning monster black holes

Fossil teeth suggest a long childhood is the prelude to the evolution of a large brain

Discovery of three galactic 'red monsters' in early universe challenges current models of galaxy formation

Barley pangenome study reveals diversity can arise after domestication

Relevant physicsforums posts, the pauli-lubanski vector and angular momentum.

Nov 12, 2024

Entropy increase in proton/proton collision?

Two-electrons lagrangian in qed.

Nov 11, 2024

Is space-time curvature a curvature of the Higgs field?

Nov 8, 2024

Relativity Considerations for Measurements on a Free Particle

How to derive momentum operator in position basis via its definition.

Nov 7, 2024

More from Quantum Physics

Related Stories

Developing the next generation of quantum algorithms and materials

Jun 6, 2022

A world first: Qubit coherence decay traced to thermal dissipation

Aug 22, 2024

Cosmic rays may soon stymie quantum computing

Aug 26, 2020

Quantum challenge to be solved one mile underground

Apr 29, 2024

New superconducting qubit testbed benefits quantum information science development

Sep 29, 2022

Novel superconducting flux qubit can operate without being surrounded by a magnetic field

Oct 17, 2024

Recommended for you

Researchers demonstrate universal control of a quantum dot-based system with four singlet-triplet qubits

13 hours ago

Unique magnetic properties of 2D triangular lattice materials have potential applications for quantum computing

8 hours ago

Lattice QCD method suggests a simpler spectrum of exotic XYZ hadrons

Scientists demonstrate controlled transfer of atoms using coherent tunneling between optical tweezers

Compact error correction: Toward a more efficient 'quantum hard drive'

Implementing topologically ordered time crystals on quantum processors

Nov 9, 2024

Let us know if there is a problem with our content

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter

International Conference on Atomic Physics (ICAP) Summer School 2022

The International Conference on Atomic Physics (ICAP) Summer School is a satellite meeting to the  ICAP 2022 Conference  being held in Toronto, July 17 – 22, 2022.

The topics covered include:

• Atomic quantum gases
• Cold molecules and quantum chemistry
• AMO Physics and topology
• Quantum sensing and metrology
• Quantum computing and quantum simulation
• Quantum nanophotonics
• Strongly correlated quantum systems: Theoretical approaches

Kyung Soo Choi, Department of Physics and Astronomy (Co-Chair)

Crystal Senko, Department of Physics and Astronomy (Co-Chair)

Michal Bajcsy, Department of Electrical Engineering

Rajibul Islam,  Department of Physics and Astronomy

Alan Jamison, Department of Physics and Astronomy

Christine Muschik, Department of Physics and Astronomy

• Wolfgang Ketterle - John D. MacArthur Professor of Physics Director, MIT-Harvard Center for Ultracold Atoms - Massachusetts Institute of Technology
• Michael Kohl - Alexander-von-Humboldt Professor, University of Bonn
• Mikhail Lukin - George Vasmer Leverett Professor of Physics, Harvard University
• Baptiste Royer - Faculty, Institut quantique, Université de Sherbrooke
• Giulia Semeghini - MPHQ Postdoctoral Fellow, Harvard University
• Masahito Ueda - Professor, The University of Tokyo
• Tanya Zelevinsky - Associate Professor, Columbia University

Michael Kohl, University of Bonn

In these lectures we are going to review the physics of ultracold fermionic atoms in optical lattices. We start from the basic principles of non-interacting Fermions in a band structure. Subsequently, we will move on to interacting systems and discuss the Mott insulator and anti-ferromagnetic order. The discussion of preparation and detection techniques of complex quantum states and current experiments completes the lectures.

Mikhail Lukin and Giulia Semeghini, Harvard University

Programmable quantum simulations and quantum information processing based on Rydberg atom arrays

We will discuss the recent advances involving programmable, coherent manipulation of quantum many-body systems using neutral atom arrays excited into Rydberg states, allowing the control over 200 qubits in two dimensions. These systems can be used for realization and probing of exotic quantum phases of matter and exploration of their non-equilibrium dynamics. Recent advances involving the realization and probing of quantum spin liquid states - the exotic topological states of matter have thus far evaded direct experimental detection and the observation of quantum speedup for solving optimization problems will be described. In addition, the realization of novel quantum processing architecture based on dynamically reconfigurable entanglement and the steps towards quantum error correction will be discussed. Finally, we will discuss prospects for using these techniques for realization of large-scale quantum simulators and processors.

Masahito Ueda, The University of Tokyo

Non-Hermitian Physics

Beyond-hermitian physics has recently attracted a great deal of attention due to remarkable advances in experimental techniques and theoretical methods in AMO, condensed matter and nonequilibrium statistical physics. Complete knowledge about quantum jumps allows a description of quantum dynamics at the single-trajectory level. A subclass thereof without quantum jumps can be described by a non-hermitian Hamiltonian. Here, symmetry, topology and many-body effects are fundamentally altered. Importantly, transposition and complex conjugation, which are equivalent in hermitian physics, become inequivalent, leading to proliferation of new topological phases and symmetry classes. In random matrix theory, transposition symmetry leads to two new universality classes of level-spacing statistics other than the Ginibre ensemble. In many-body physics, non-hermiticity leads to the dynamical sign reversal of magnetism in dissipative Hubbard models, violation of the g-theorem in the Kondo problem, and quantum phase transitions without gap closing. In the lecture, I will provide an overview on the fundamentals and new frontiers about beyond-Hermitian quantum physics.

Ref.  Y. Ashida, Z. Gong, and M. Ueda, Adv. Phys.  69 , 249 (2021)

Baptiste Boyer, Université de Sherbrooke

Encoding quantum information in states of light: bosonic codes in circuit QED

The main approach to quantum computing is to encode logical information in ensembles of physical two-level systems such as superconducting qubits or trapped ions. Another promising strategy is rather to encode the information in a harmonic oscillator using a bosonic code. Because of the simplicity of these physical systems, harmonic oscillators are often longer-lived than physical qubits, and have simpler error models. Moreover, their large Hilbert space (formally infinite) allows to redundantly encode the information using a small amount of hardware.In these lectures, I will introduce these bosonic codes and some related topics. I will discuss the main codes that are studied today, how to prepare the code words, how to perform logical operations and how to visualize them.

Quantum Thermalization

Ultracold atomic physics has offered a fresh view about why isolated quantum systems thermalize without thermal reservoirs. This question dates back to von Neumann’s original attempt to derive the second law of thermodynamics from quantum mechanics. Quantum thermalization also has a close link with quantum information because thermalization proceeds in Hilbert space rather than phase space via quantum entanglement. Moreover, recent advances in quantum gas microscopy has enabled one to observe single-shot measurement of a quantum many-body wavefunction at the level of single atoms. In this regime, measurement backaction cannot be ignored and we are led to reconsider the foundation of statistical mechanics to incorporate measurement backaction and ponder whether thermalization occurs at the level of single quantum trajectories. This question is relevant to quantum computation. In the lecture, I will give a brief introduction of quantum thermalization and review some of the recent experiments in ultracold atoms.

Wolfgang Ketterle, Massachusetts Institute of Technology

Wednesday, july 13.

Superfluidity, Bogoliubov excitations and the superfluid-to-Mott-insulator transition in optical lattices In this lecture, we start out with the weakly interacting Bose gas and its excitation spectrum.  We discuss the limiting cases of bosons in weak and strong lattices, and then describe the quantum phase transition between those two limits.

Friday, July 15

Spin physics of ultracold atoms in optical lattices Starting from the Bose-Hubbard model, we derive spin Hamiltonians where spin-spin interactions arise due to superexchange.  Heisenberg spin models, where only neighboring spins interact, are the paradigmatic model for many interesting phenomena.  Using lithium-7 atoms and Feshbach resonances to tune the interactions, one can create spin ½ Heisenberg models with adjustable anisotropy, including the special XX-model which can be exactly solved by mapping it to non-interacting fermions.  Spin transport changes from ballistic to diffusive depending on the anisotropy.  For transverse spin patterns, a superexchange induced effective magnetic field causes dephasing.  Spin helices can be  exact eigenstates for special values of their winding angle and are called phantom helix states since they contribute momentum, but no energy.

Tanya Zelevinsky, Columbia University

Cold molecules for fundamental physics and chemistry

Techniques for controlling quantum states of atoms have led to extremely precise metrology, studies of degenerate gases, and new quantum information technologies. Extending such techniques to molecules further enriches the understanding of fundamental physics, basic chemical processes, and many-body science. Samples of ultracold molecules can be created by binding laser-cooled atoms, or by direct cooling. We cover very basic properties of molecules and discuss applications of cold molecules in fundamental physics and chemistry.

Tuesday Industry Panel

Philippe Bouyer, MuQuans

Jim Shaffer, QVIL

Will Lunden, Vector Atomic

Georg Raithel and David Anderson, Rydberg Technologies

Moderator: John Donohue, Institute for Quantum Computing

Wednesday Industry Panel

Tom Noel, ColdQuanta

Justin Ging and Krish Kotru, Atom Computing

Tony Ransford, Quantinuum

Harry Levine, Amazon AWS Quantum

Perimeter Institute for Theoretical Physics

Transformative Quantum Technologies

Quantum Nanophotonic Initiative Program

MIT-Harvard Center for Ultracold Atoms

Institute for Quantum Computing

Help | Advanced Search

Quantum Physics

Title: experimental secure multiparty computation from quantum oblivious transfer with bit commitment.

Abstract: Secure multiparty computation enables collaborative computations across multiple users while preserving individual privacy, which has a wide range of applications in finance, machine learning and healthcare. Secure multiparty computation can be realized using oblivious transfer as a primitive function. In this paper, we present an experimental implementation of a quantum-secure quantum oblivious transfer (QOT) protocol using an adapted quantum key distribution system combined with a bit commitment scheme, surpassing previous approaches only secure in the noisy storage model. We demonstrate the first practical application of the QOT protocol by solving the private set intersection, a prime example of secure multiparty computation, where two parties aim to find common elements in their datasets without revealing any other information. In our experiments, two banks can identify common suspicious accounts without disclosing any other data. This not only proves the experimental functionality of QOT, but also showcases its real-world commercial applications.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• INSPIRE HEP
• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .