what does hypothesis mean in geometry

A statement that could be true, which might then be tested.

Example: Sam has a hypothesis that "large dogs are better at catching tennis balls than small dogs". We can test that hypothesis by having hundreds of different sized dogs try to catch tennis balls.

Sometimes the hypothesis won't be tested, it is simply a good explanation (which could be wrong). Conjecture is a better word for this.

Example: you notice the temperature drops just as the sun rises. Your hypothesis is that the sun warms the air high above you, which rises up and then cooler air comes from the sides.

Note: when someone says "I have a theory" they should say "I have a hypothesis", because in mathematics a theory is actually well proven.

Definition Of Hypothesis

Hypothesis is the part of a conditional statement just after the word if.

Examples of Hypothesis

In the conditional, "If all fours sides of a quadrilateral measure the same, then the quadrilateral is a square" the hypothesis is "all fours sides of a quadrilateral measure the same".

Video Examples: Hypothesis  

Solved Example on Hypothesis

Ques:  in the example above, is the hypothesis "all fours sides of a quadrilateral measure the same" always, never, or sometimes true.

A. always B. never C. sometimes Correct Answer: C

Step 1: The hypothesis is sometimes true. Because, its true only for a square and a rhombus, not for the other quadrilaterals rectangle, parallelogram, or trapezoid.

Related Worksheet

• Identifying-and-Describing-Right-Triangles-Gr-4
• Points,-Lines,-Line-Segments,-Rays-and-Angles-Gr-4
• Two-dimensional-Geometric-Figures-Gr-4
• Interpreting-Multiplication-as-Scaling-or-Resizing-Gr-5
• Parallel-Lines-and-Transversals-Gr-8

HighSchool Math

• MathDictionary
• PhysicsDictionary
• ChemistryDictionary
• BiologyDictionary
• MathArticles
• HealthInformation

A free service from Mattecentrum

If-then statement

• Logical correct I
• Logical correct II

When we previously discussed inductive reasoning we based our reasoning on examples and on data from earlier events. If we instead use facts, rules and definitions then it's called deductive reasoning.

We will explain this by using an example.

If you get good grades then you will get into a good college.

The part after the "if": you get good grades - is called a hypotheses and the part after the "then" - you will get into a good college - is called a conclusion.

Hypotheses followed by a conclusion is called an If-then statement or a conditional statement.

This is noted as

$$p \to q$$

This is read - if p then q.

A conditional statement is false if hypothesis is true and the conclusion is false. The example above would be false if it said "if you get good grades then you will not get into a good college".

If we re-arrange a conditional statement or change parts of it then we have what is called a related conditional.

Our conditional statement is: if a population consists of 50% men then 50% of the population must be women.

If we exchange the position of the hypothesis and the conclusion we get a converse statemen t: if a population consists of 50% women then 50% of the population must be men.

$$q\rightarrow p$$

If both statements are true or if both statements are false then the converse is true. A conditional and its converse do not mean the same thing

If we negate both the hypothesis and the conclusion we get a inverse statemen t: if a population do not consist of 50% men then the population do not consist of 50% women.

$$\sim p\rightarrow \: \sim q$$

The inverse is not true juest because the conditional is true. The inverse always has the same truth value as the converse.

We could also negate a converse statement, this is called a contrapositive statemen t:  if a population do not consist of 50% women then the population do not consist of 50% men.

$$\sim q\rightarrow \: \sim p$$

The contrapositive does always have the same truth value as the conditional. If the conditional is true then the contrapositive is true.

A pattern of reaoning is a true assumption if it always lead to a true conclusion. The most common patterns of reasoning are detachment and syllogism.

If we turn of the water in the shower, then the water will stop pouring.

If we call the first part p and the second part q then we know that p results in q. This means that if p is true then q will also be true. This is called the law of detachment and is noted:

$$\left [ (p \to q)\wedge p \right ] \to q$$

The law of syllogism tells us that if p → q and q → r then p → r is also true.

This is noted:

$$\left [ (p \to q)\wedge (q \to r ) \right ] \to (p \to r)$$

If the following statements are true:

If we turn of the water (p), then the water will stop pouring (q). If the water stops pouring (q) then we don't get wet any more (r).

Then the law of syllogism tells us that if we turn of the water (p) then we don't get wet (r) must be true.

Video lesson

Write a converse, inverse and contrapositive to the conditional

"If you eat a whole pint of ice cream, then you won't be hungry"

• Angles, parallel lines and transversals
• Congruent triangles
• More about triangles
• Inequalities
• Mean and geometry
• The converse of the Pythagorean theorem and special triangles
• Properties of parallelograms
• Common types of transformation
• Transformation using matrices
• Basic information about circles
• Inscribed angles and polygons
• Advanced information about circles
• Parallelogram, triangles etc
• The surface area and the volume of pyramids, prisms, cylinders and cones
• SAT Overview
• ACT Overview

Understanding the Role of Hypotheses and Conclusions in Mathematical Reasoning

Hypothesis and conclusion.

In the context of mathematics and logic, a hypothesis is a statement or proposition that is assumed to be true for the purpose of a logical argument or investigation. It is usually denoted by “H” or “P” and is the starting point for many mathematical proofs.

For example, let’s consider the hypothesis: “If it is raining outside, then the ground is wet.” This statement assumes that whenever it rains, the ground will be wet.

The conclusion, on the other hand, is the statement or proposition that is inferred or reached by logical reasoning, based on the hypothesis or given information. It is typically denoted by “C” or “Q”.

Using the same example, the conclusion derived from the hypothesis could be: “It is currently raining outside, so the ground is wet.” This conclusion is based on the assumption that the given condition of rain implies a wet ground.

In mathematics, hypotheses and conclusions are commonly used in proofs and logical arguments. By stating a hypothesis and then deducing a conclusion from it, mathematicians can demonstrate the validity of certain mathematical concepts, theorems, or formulas.

It’s important to note that in mathematics, a hypothesis is not the same as a guess or a prediction. It is a statement that is assumed to be true and serves as the basis for logical reasoning, while the conclusion is the logical consequence or outcome that is drawn from the hypothesis.

More Answers:

Recent posts, mathematics in cancer treatment.

How Mathematics is Transforming Cancer Treatment Mathematics plays an increasingly vital role in the fight against cancer mesothelioma. From optimizing drug delivery systems to personalizing

Ramses II A Prominent Pharaoh and Legacy of Ancient Egypt

Ramses II (c. 1279–1213 BCE) Ramses II, also known as Ramses the Great, was one of the most prominent and powerful pharaohs of ancient Egypt.

Formula for cyclic adenosine monophosphate & Its Significance

Is the formula of cyclic adenosine monophosphate (cAMP) $ce{C_{10}H_{11}N_{5}O_{6}P}$ or $ce{C_{10}H_{12}N_{5}O_{6}P}$? Does it matter? The correct formula for cyclic adenosine monophosphate (cAMP) is $ce{C_{10}H_{11}N_{5}O_{6}P}$. The

Development of a Turtle Inside its Egg

How does a turtle develop inside its egg? The development of a turtle inside its egg is a fascinating process that involves several stages and

The Essential Molecule in Photosynthesis for Energy and Biomass

Why does photosynthesis specifically produce glucose? Photosynthesis is the biological process by which plants, algae, and some bacteria convert sunlight, carbon dioxide (CO2), and water

• Number System and Arithmetic
• Probability
• Mensuration
• Trigonometry
• Mathematics

Hypothesis | Definition, Meaning and Examples

Hypothesis is a hypothesis is fundamental concept in the world of research and statistics. It is a testable statement that explains what is happening or observed. It proposes the relation between the various participating variables.

Hypothesis is also called Theory, Thesis, Guess, Assumption, or Suggestion . Hypothesis creates a structure that guides the search for knowledge.

In this article, we will learn what hypothesis is, its characteristics, types, and examples. We will also learn how hypothesis helps in scientific research.

Table of Content

What is Hypothesis?

Characteristics of hypothesis, sources of hypothesis, types of hypothesis, functions of hypothesis, how hypothesis help in scientific research.

Hypothesis is a suggested idea or an educated guess or a proposed explanation made based on limited evidence, serving as a starting point for further study. They are meant to lead to more investigation.

It's mainly a smart guess or suggested answer to a problem that can be checked through study and trial. In science work, we make guesses called hypotheses to try and figure out what will happen in tests or watching. These are not sure things but rather ideas that can be proved or disproved based on real-life proofs. A good theory is clear and can be tested and found wrong if the proof doesn't support it.

Hypothesis Meaning

A hypothesis is a proposed statement that is testable and is given for something that happens or observed.

• It is made using what we already know and have seen, and it's the basis for scientific research.
• A clear guess tells us what we think will happen in an experiment or study.
• It's a testable clue that can be proven true or wrong with real-life facts and checking it out carefully.
• It usually looks like a "if-then" rule, showing the expected cause and effect relationship between what's being studied.

Here are some key characteristics of a hypothesis:

• Testable: An idea (hypothesis) should be made so it can be tested and proven true through doing experiments or watching. It should show a clear connection between things.
• Specific: It needs to be easy and on target, talking about a certain part or connection between things in a study.
• Falsifiable: A good guess should be able to show it's wrong. This means there must be a chance for proof or seeing something that goes against the guess.
• Logical and Rational: It should be based on things we know now or have seen, giving a reasonable reason that fits with what we already know.
• Predictive: A guess often tells what to expect from an experiment or observation. It gives a guide for what someone might see if the guess is right.
• Concise: It should be short and clear, showing the suggested link or explanation simply without extra confusion.
• Grounded in Research: A guess is usually made from before studies, ideas or watching things. It comes from a deep understanding of what is already known in that area.
• Flexible: A guess helps in the research but it needs to change or fix when new information comes up.
• Relevant: It should be related to the question or problem being studied, helping to direct what the research is about.
• Empirical: Hypotheses come from observations and can be tested using methods based on real-world experiences.

Hypotheses can come from different places based on what you're studying and the kind of research. Here are some common sources from which hypotheses may originate:

• Existing Theories: Often, guesses come from well-known science ideas. These ideas may show connections between things or occurrences that scientists can look into more.
• Observation and Experience: Watching something happen or having personal experiences can lead to guesses. We notice odd things or repeat events in everyday life and experiments. This can make us think of guesses called hypotheses.
• Previous Research: Using old studies or discoveries can help come up with new ideas. Scientists might try to expand or question current findings, making guesses that further study old results.
• Literature Review: Looking at books and research in a subject can help make guesses. Noticing missing parts or mismatches in previous studies might make researchers think up guesses to deal with these spots.
• Problem Statement or Research Question: Often, ideas come from questions or problems in the study. Making clear what needs to be looked into can help create ideas that tackle certain parts of the issue.
• Analogies or Comparisons: Making comparisons between similar things or finding connections from related areas can lead to theories. Understanding from other fields could create new guesses in a different situation.
• Hunches and Speculation: Sometimes, scientists might get a gut feeling or make guesses that help create ideas to test. Though these may not have proof at first, they can be a beginning for looking deeper.
• Technology and Innovations: New technology or tools might make guesses by letting us look at things that were hard to study before.
• Personal Interest and Curiosity: People's curiosity and personal interests in a topic can help create guesses. Scientists could make guesses based on their own likes or love for a subject.

Here are some common types of hypotheses:

Simple Hypothesis

Complex hypothesis, directional hypothesis.

• Non-directional Hypothesis

Null Hypothesis (H0)

Alternative hypothesis (h1 or ha), statistical hypothesis, research hypothesis, associative hypothesis, causal hypothesis.

Simple Hypothesis guesses a connection between two things. It says that there is a connection or difference between variables, but it doesn't tell us which way the relationship goes. Example: Studying more can help you do better on tests. Getting more sun makes people have higher amounts of vitamin D.

Complex Hypothesis tells us what will happen when more than two things are connected. It looks at how different things interact and may be linked together. Example: How rich you are, how easy it is to get education and healthcare greatly affects the number of years people live. A new medicine's success relies on the amount used, how old a person is who takes it and their genes.

Directional Hypothesis says how one thing is related to another. For example, it guesses that one thing will help or hurt another thing. Example: Drinking more sweet drinks is linked to a higher body weight score. Too much stress makes people less productive at work.

Non-Directional Hypothesis

Non-Directional Hypothesis are the one that don't say how the relationship between things will be. They just say that there is a connection, without telling which way it goes. Example: Drinking caffeine can affect how well you sleep. People often like different kinds of music based on their gender.

Null hypothesis is a statement that says there's no connection or difference between different things. It implies that any seen impacts are because of luck or random changes in the information. Example: The average test scores of Group A and Group B are not much different. There is no connection between using a certain fertilizer and how much it helps crops grow.

Alternative Hypothesis is different from the null hypothesis and shows that there's a big connection or gap between variables. Scientists want to say no to the null hypothesis and choose the alternative one. Example: Patients on Diet A have much different cholesterol levels than those following Diet B. Exposure to a certain type of light can change how plants grow compared to normal sunlight.

Statistical Hypothesis are used in math testing and include making ideas about what groups or bits of them look like. You aim to get information or test certain things using these top-level, common words only. Example: The average smarts score of kids in a certain school area is 100. The usual time it takes to finish a job using Method A is the same as with Method B.

Research Hypothesis comes from the research question and tells what link is expected between things or factors. It leads the study and chooses where to look more closely. Example: Having more kids go to early learning classes helps them do better in school when they get older. Using specific ways of talking affects how much customers get involved in marketing activities.

Associative Hypothesis guesses that there is a link or connection between things without really saying it caused them. It means that when one thing changes, it is connected to another thing changing. Example: Regular exercise helps to lower the chances of heart disease. Going to school more can help people make more money.

Causal Hypothesis are different from other ideas because they say that one thing causes another. This means there's a cause and effect relationship between variables involved in the situation. They say that when one thing changes, it directly makes another thing change. Example: Playing violent video games makes teens more likely to act aggressively. Less clean air directly impacts breathing health in city populations.

Hypotheses have many important jobs in the process of scientific research. Here are the key functions of hypotheses:

• Guiding Research: Hypotheses give a clear and exact way for research. They act like guides, showing the predicted connections or results that scientists want to study.
• Formulating Research Questions: Research questions often create guesses. They assist in changing big questions into particular, checkable things. They guide what the study should be focused on.
• Setting Clear Objectives: Hypotheses set the goals of a study by saying what connections between variables should be found. They set the targets that scientists try to reach with their studies.
• Testing Predictions: Theories guess what will happen in experiments or observations. By doing tests in a planned way, scientists can check if what they see matches the guesses made by their ideas.
• Providing Structure: Theories give structure to the study process by arranging thoughts and ideas. They aid scientists in thinking about connections between things and plan experiments to match.
• Focusing Investigations: Hypotheses help scientists focus on certain parts of their study question by clearly saying what they expect links or results to be. This focus makes the study work better.
• Facilitating Communication: Theories help scientists talk to each other effectively. Clearly made guesses help scientists to tell others what they plan, how they will do it and the results expected. This explains things well with colleagues in a wide range of audiences.
• Generating Testable Statements: A good guess can be checked, which means it can be looked at carefully or tested by doing experiments. This feature makes sure that guesses add to the real information used in science knowledge.
• Promoting Objectivity: Guesses give a clear reason for study that helps guide the process while reducing personal bias. They motivate scientists to use facts and data as proofs or disprovals for their proposed answers.
• Driving Scientific Progress: Making, trying out and adjusting ideas is a cycle. Even if a guess is proven right or wrong, the information learned helps to grow knowledge in one specific area.

Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:

• Initiating Investigations: Hypotheses are the beginning of science research. They come from watching, knowing what's already known or asking questions. This makes scientists make certain explanations that need to be checked with tests.
• Formulating Research Questions: Ideas usually come from bigger questions in study. They help scientists make these questions more exact and testable, guiding the study's main point.
• Setting Clear Objectives: Hypotheses set the goals of a study by stating what we think will happen between different things. They set the goals that scientists want to reach by doing their studies.
• Designing Experiments and Studies: Assumptions help plan experiments and watchful studies. They assist scientists in knowing what factors to measure, the techniques they will use and gather data for a proposed reason.
• Testing Predictions: Ideas guess what will happen in experiments or observations. By checking these guesses carefully, scientists can see if the seen results match up with what was predicted in each hypothesis.
• Analysis and Interpretation of Data: Hypotheses give us a way to study and make sense of information. Researchers look at what they found and see if it matches the guesses made in their theories. They decide if the proof backs up or disagrees with these suggested reasons why things are happening as expected.
• Encouraging Objectivity: Hypotheses help make things fair by making sure scientists use facts and information to either agree or disagree with their suggested reasons. They lessen personal preferences by needing proof from experience.
• Iterative Process: People either agree or disagree with guesses, but they still help the ongoing process of science. Findings from testing ideas make us ask new questions, improve those ideas and do more tests. It keeps going on in the work of science to keep learning things.

People Also View:

Mathematics Maths Formulas Branches of Mathematics

Hypothesis is a testable statement serving as an initial explanation for phenomena, based on observations, theories, or existing knowledge . It acts as a guiding light for scientific research, proposing potential relationships between variables that can be empirically tested through experiments and observations.

The hypothesis must be specific, testable, falsifiable, and grounded in prior research or observation, laying out a predictive, if-then scenario that details a cause-and-effect relationship. It originates from various sources including existing theories, observations, previous research, and even personal curiosity, leading to different types, such as simple, complex, directional, non-directional, null, and alternative hypotheses, each serving distinct roles in research methodology .

The hypothesis not only guides the research process by shaping objectives and designing experiments but also facilitates objective analysis and interpretation of data , ultimately driving scientific progress through a cycle of testing, validation, and refinement.

Hypothesis - FAQs

What is a hypothesis.

A guess is a possible explanation or forecast that can be checked by doing research and experiments.

What are Components of a Hypothesis?

The components of a Hypothesis are Independent Variable, Dependent Variable, Relationship between Variables, Directionality etc.

What makes a Good Hypothesis?

Testability, Falsifiability, Clarity and Precision, Relevance are some parameters that makes a Good Hypothesis

Can a Hypothesis be Proven True?

You cannot prove conclusively that most hypotheses are true because it's generally impossible to examine all possible cases for exceptions that would disprove them.

How are Hypotheses Tested?

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data

Can Hypotheses change during Research?

Yes, you can change or improve your ideas based on new information discovered during the research process.

What is the Role of a Hypothesis in Scientific Research?

Hypotheses are used to support scientific research and bring about advancements in knowledge.

Similar Reads

• Hypothesis | Definition, Meaning and Examples Hypothesis is a hypothesis is fundamental concept in the world of research and statistics. It is a testable statement that explains what is happening or observed. It proposes the relation between the various participating variables. Hypothesis is also called Theory, Thesis, Guess, Assumption, or Sug 12 min read
• Alternative Hypothesis: Definition, Types and Examples In statistical hypothesis testing, the alternative hypothesis is an important proposition in the hypothesis test. The goal of the hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting the credibility of the alternative hypothesis instead of the defaul 7 min read
• Level of Significance-Definition, Steps and Examples Level of significance or Statistical significance is an important terminology used in Statistics. Level of significance is the measurement of the statistical significance. The level of significance explains whether the null hypothesis is accepted or rejected. In this article, we are going to discuss 7 min read
• Cell Theory Notes - Definition, Parts, History, & Examples Cell Theory is a foundational biological principle stating that all living organisms are composed of cells, the cell is the basic unit of life, and all cells arise from pre-existing cells. Developed by scientists Schleiden, Schwann, and Virchow in the 19th century, this theory underscores the role o 8 min read
• First Derivative: Definition, Formulas, and Examples First Derivative Test is the test in calculus to find whether a function has a maximum or minimum value in the given interval. As the name suggests, the first derivative is used in this test to find the critical point and then further conditions are used to check each critical point for extrema. Man 14 min read
• Hypothesis Testing Formula Statistics is a discipline of applied mathematics that deals with gathering, describing, analyzing, and inferring conclusions from numerical data. Differential and integral calculus, linear algebra, and probability theory are all used substantially in statistics' mathematical theories. Statisticians 8 min read
• Difference Between Hypothesis And Theory Understanding the difference between a hypothesis and a theory is important in scientific research. A hypothesis is an educated guess or proposed explanation for a phenomenon, based on limited evidence and requiring further investigation. While, a theory is a well-substantiated explanation of an asp 5 min read
• Real-life Applications of Hypothesis Testing Hypothesis testing is a fundamental statistical concept that helps us to conclude larger groups based on smaller samples. It offers a systematic approach to conclude population characteristics from observed sample data. It's like making educated guesses and then collecting data to see if our guesses 6 min read
• Econometrics : Meaning, Examples, Theory and Methods What is Econometrics?Econometrics is a branch of economics that applies statistical methods and mathematical models to analyze economic data. It combines economic theory, mathematics, and statistical techniques to quantify and test hypotheses about economic relationships. Econometric analysis is use 10 min read
• Real Life Examples and Applications of Power Set The concept of power sets is a fundamental topic in set theory with a wide range of real-life applications. A power set is essentially a set of all possible subsets of a given set, including the empty set and the set itself. This means if you have a set with three elements, its power set will contai 6 min read
• How do you define and measure your product hypothesis? Hypothesis in product management is like making an educated guess or assumption about something related to a product, such as what users need or how a new feature might work. It's a statement that you can test to see if it's true or not, usually by trying out different ideas and seeing what happens. 11 min read
• What are Descriptive Analytics? Working and Examples Descriptive analytics helps to identify important patterns and trends in large datasets. In comparison to all other methods of data analysis, descriptive is the most used one. The main task of descriptive analytics is to create metrics and key performance indicators for use in dashboards and busines 10 min read
• Equal Sets: Definition, Cardinality, and Venn Diagram Equal Set is the relation between two sets that tells us about the equality of two sets i.e., all the elements of both sets are the same and both sets have the same number of elements as well. As we know, a set is a well-defined collection of objects where no two objects can be the same, and sets ca 9 min read
• What is Binomial Probability Distribution with Example? In a binomial distribution, the probability of achieving success must stay consistent across the trials being examined. For instance, when tossing a coin, the probability of landing heads is always ½ for each trial, as there are only two possible outcomes.Explanation: Probability is the likelihood o 6 min read
• What is Spontaneity? - Definition, Types, Gibbs Energy Thermodynamics is a discipline of physics that studies heat, work, and temperature, as well as their relationships with energy, radiation, and matter's physical characteristics. The four principles of thermodynamics regulate the behaviour of these quantities, which provide a quantitative description 7 min read
• Set Theory - Definition, Types, Operations Set Theory is a branch of logical mathematics that studies the collection of objects and operations based on it. A set is simply a collection of objects or a group of objects. For example, a group of players in a football team is a set and the players in the team are its objects. The words collectio 10 min read
• Probability Theorems | Theorems and Examples What is Probability?Probability can be defined as the possibility of occurrence of an event. Probability is the likelihood or the chances that an uncertain event will occur. The probability of an event always lies between 0 and 1. [Tex]Probability(P)=\frac{Favourable~Outcomes}{Total~Outcomes} [/Tex] 10 min read
• Introduction of Statistics and its Types Statistics and its Types: Statistics is a branch of math focused on collecting, organizing, and understanding numerical data. It involves analyzing and interpreting data to solve real-life problems, using various quantitative models. Some view statistics as a separate scientific discipline rather th 15+ min read
• Collection and Presentation of Data We come across a lot of information every day from different sources. Our newspapers, TV, Phone and the Internet, etc are the sources of information in our life. This information can be related to anything, from bowling averages in cricket to profits of the company over the years. These facts and fi 10 min read
• Geeks Premier League
• School Learning
• Geeks Premier League 2023
• Maths-Class-12

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Hypothesis | Definition & Meaning

JUMP TO TOPIC

Explanation of Hypothesis

Contradiction, simple hypothesis, complex hypothesis, null hypothesis, alternative hypothesis, empirical hypothesis, statistical hypothesis, special example of hypothesis, solution part (a), solution part (b), hypothesis|definition & meaning.

A hypothesis is a claim or statement  that makes sense in the context of some information or data at hand but hasn’t been established as true or false through experimentation or proof.

In mathematics, any statement or equation that describes some relationship between certain variables can be termed as hypothesis if it is consistent with some initial supporting data or information, however, its yet   to be proven true or false by some definite and trustworthy experiment or mathematical law. 

Following example illustrates one such hypothesis to shed some light on this very fundamental concept which is often used in different areas of mathematics.

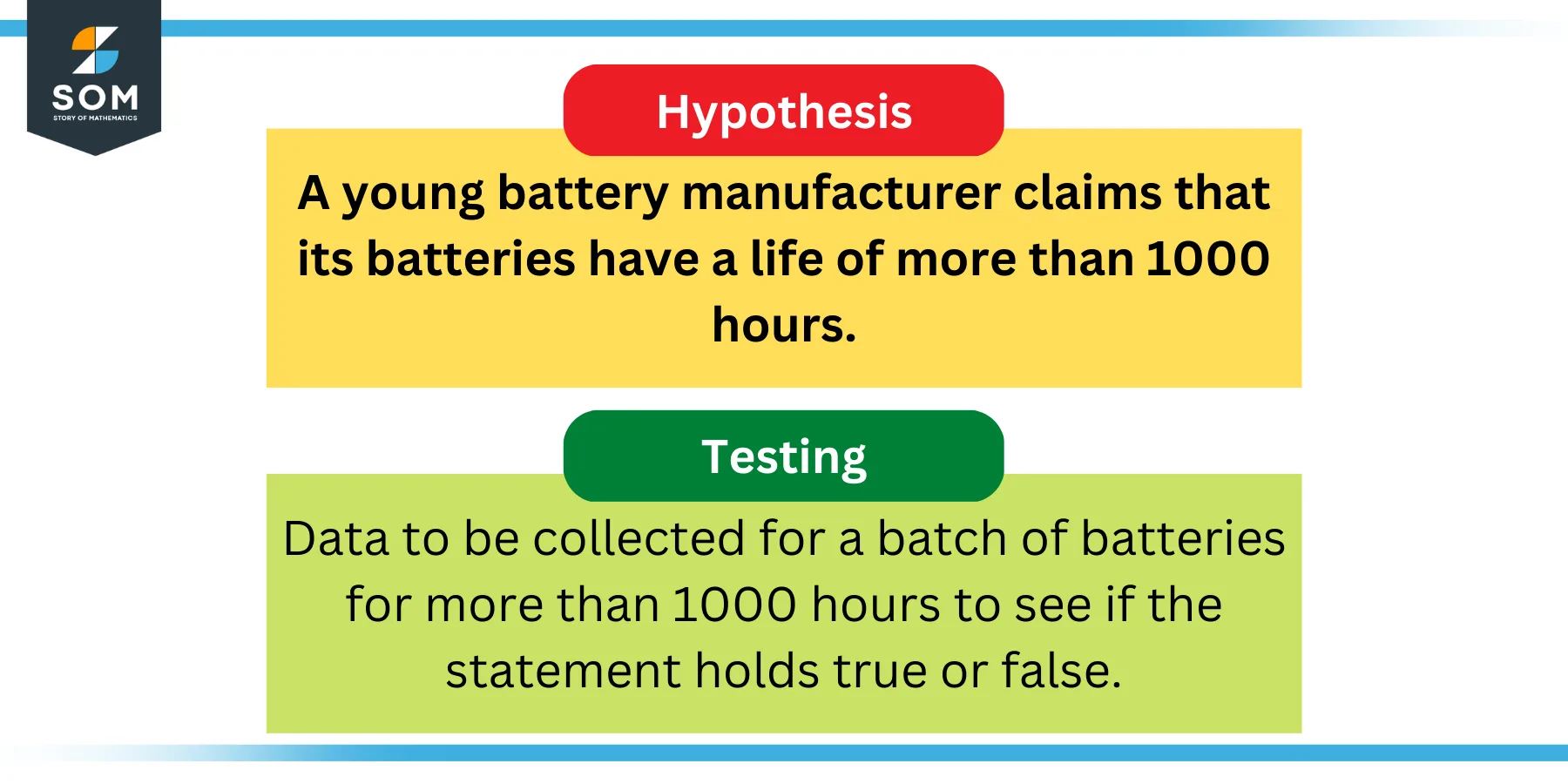
Figure 1: Example of Hypothesis

Here we have considered an example of a young startup company that manufactures state of the art batteries. The hypothesis or the claim of the company is that their batteries have a mean life of more than 1000 hours. Now its very easy to understand that they can prove their claim on some testing experiment in their lab.

However, the statement can only be proven if and only if at least one batch of their production batteries have actually been deployed in the real world for more than 1000 hours . After 1000 hours, data needs to be collected and it needs to be seen what is the probability of this statement being true .

The following paragraphs further explain this concept.

As explained with the help of an example earlier, a hypothesis in mathematics is an untested claim that is backed up by all the known data or some other discoveries or some weak experiments.

In any mathematical discovery, we first start by assuming something or some relationship . This supposed statement is called a supposition. A supposition, however, becomes a hypothesis when it is supported by all available data and a large number of contradictory findings.

The hypothesis is an important part of the scientific method that is widely known today for making new discoveries. The field of mathematics inherited this process. Following figure shows this cycle as a graphic:

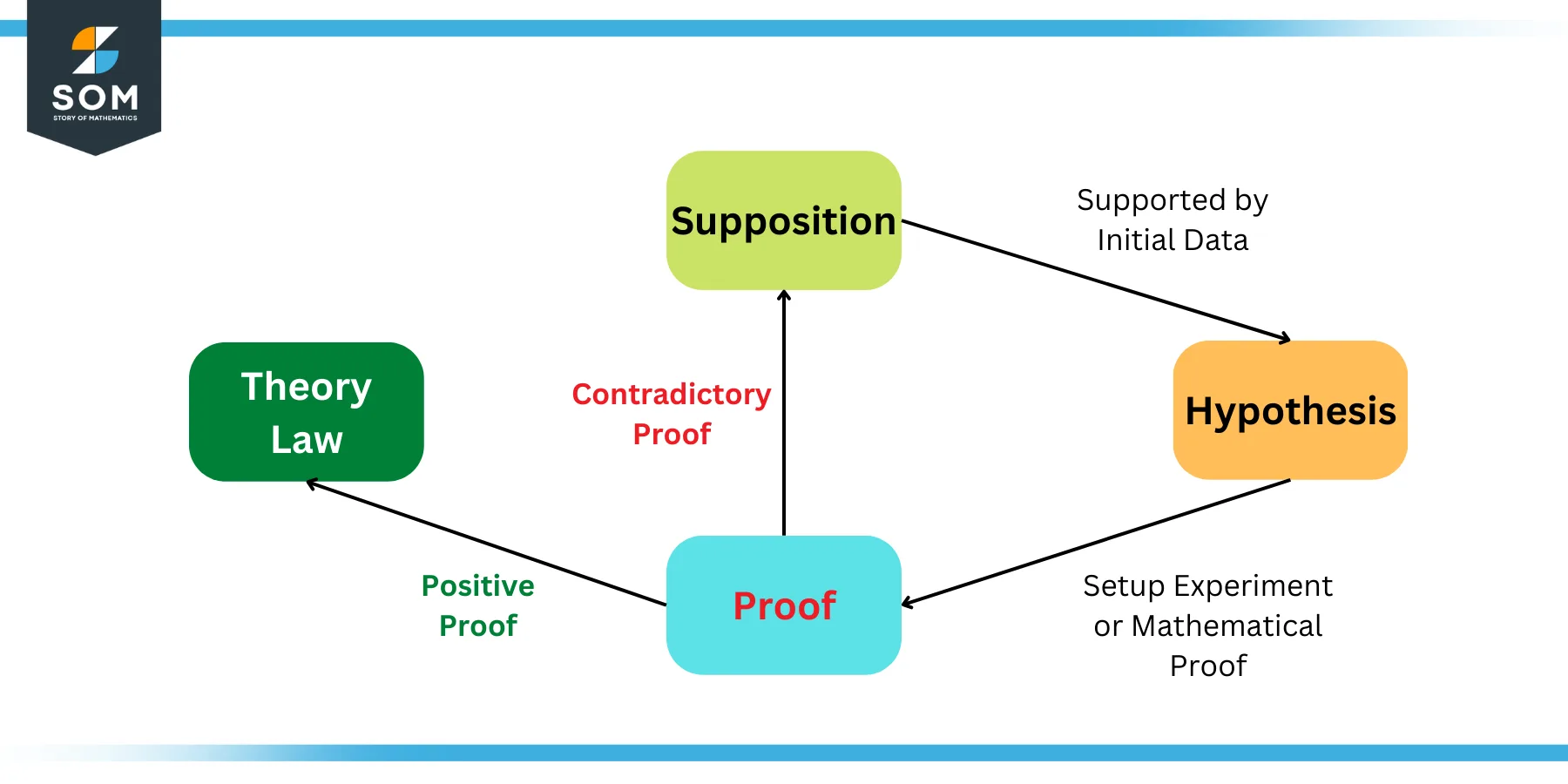
Figure 2: Role of Hypothesis in the Scientific Method 

The above figure shows a simplified version of the scientific method. It shows that whenever a supposition is supported by some data, its termed as hypothesis. Once a hypothesis is proven by some well known and widely acceptable experiment or proof, its becomes a law. If the hypothesis is rejected by some contradictory results then the supposition is changed and the cycle continues.

Lets try to understand the scientific method and the hypothesis concept with the help of an example. Lets say that a teacher wanted to analyze the relationship between the students performance in a certain subject, lets call it A, based on whether or not they studied a minor course, lets call it B.

Now the teacher puts forth a supposition that the students taking the course B prior to course A must perform better in the latter due to the obvious linkages in the key concepts. Due to this linkage, this supposition can be termed as a hypothesis.

However to test the hypothesis, the teacher has to collect data from all of his/her students such that he/she knows which students have taken course B and which ones haven’t. Then at the end of the semester, the performance of the students must be measured and compared with their course B enrollments.

If the students that took course B prior to course A perform better, then the hypothesis concludes successful . Otherwise, the supposition may need revision.

The following figure explains this problem graphically.

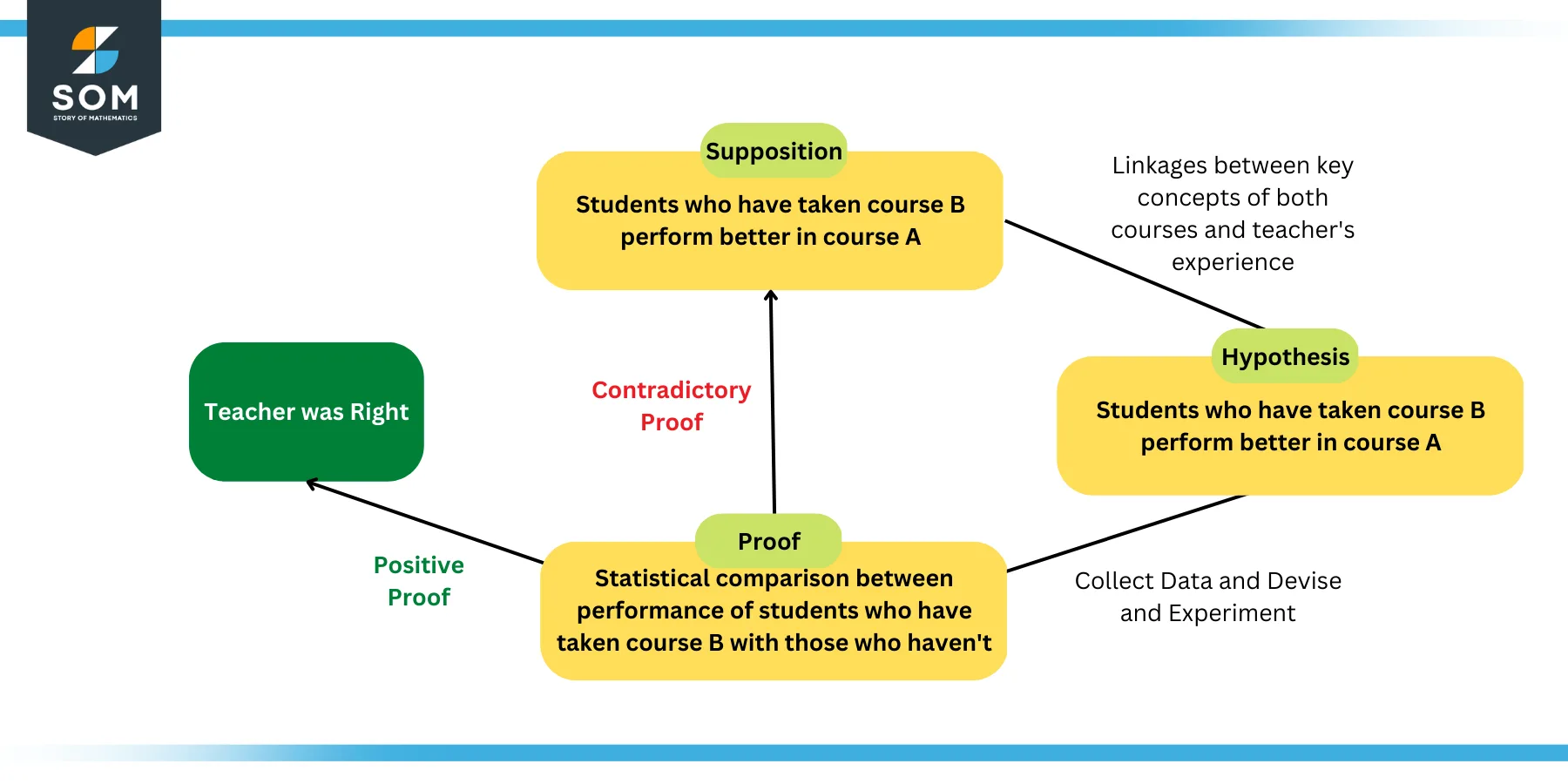
Figure 3: Teacher and Course Example of Hypothesis

Important Terms Related to Hypothesis

To further elaborate the concept of hypothesis, we first need to understand a few key terms that are widely used in this area such as conjecture, contradiction and some special types of hypothesis (simple, complex, null, alternative, empirical, statistical). These terms are briefly explained below:

A conjecture is a term used to describe a mathematical assertion that has notbeenproved. While testing   may occasionally turn up millions of examples in favour of a conjecture, most experts in the area will typically only accept a proof . In mathematics, this term is synonymous to the term hypothesis.

In mathematics, a contradiction occurs if the results of an experiment or proof are against some hypothesis.  In other words, a contradiction discredits a hypothesis.

A simple hypothesis is such a type of hypothesis that claims there is a correlation between two variables. The first is known as a dependent variable while the second is known as an independent variable.

A complex hypothesis is such a type of hypothesis that claims there is a correlation between more than two variables.  Both the dependent and independent variables in this hypothesis may be more than one in numbers.

A null hypothesis, usually denoted by H0, is such a type of hypothesis that claims there is no statistical relationship and significance between two sets of observed data and measured occurrences for each set of defined, single observable variables. In short the variables are independent.

An alternative hypothesis, usually denoted by H1 or Ha, is such a type of hypothesis where the variables may be statistically influenced by some unknown factors or variables. In short the variables are dependent on some unknown phenomena .

An Empirical hypothesis is such a type of hypothesis that is built on top of some empirical data or experiment or formulation.

A statistical hypothesis is such a type of hypothesis that is built on top of some statistical data or experiment or formulation. It may be logical or illogical in nature.

According to the Riemann hypothesis, only negative even integers and complex numbers with real part 1/2 have zeros in the Riemann zeta function . It is regarded by many as the most significant open issue in pure mathematics.

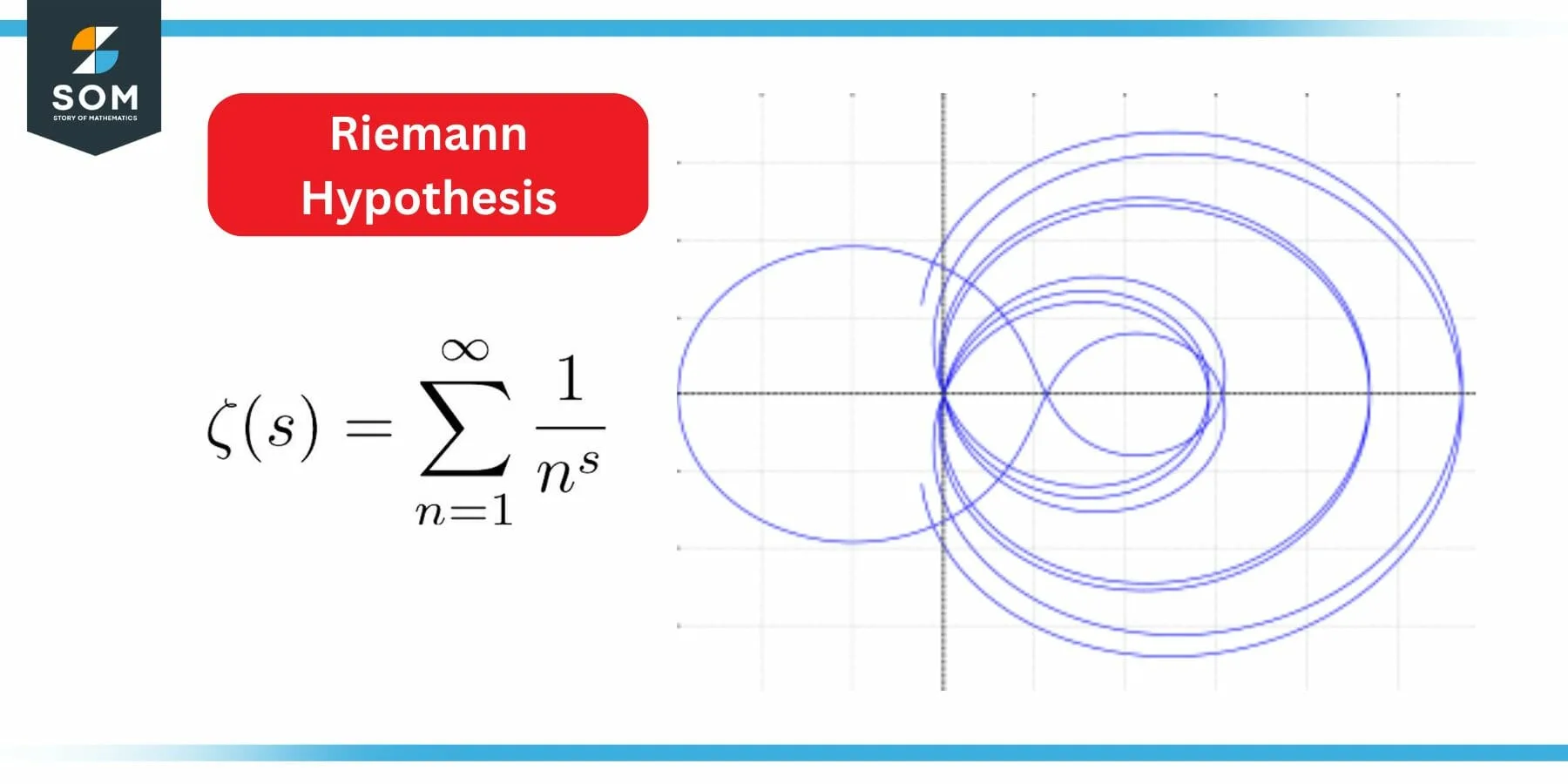
Figure 4: Riemann Hypothesis

The Riemann hypothesis is the most well-known mathematical conjecture, and it has been the subject of innumerable proof efforts.

Numerical Examples

Identify the conclusions and hypothesis in the following given statements. Also state if the conclusion supports the hypothesis or not.

Part (a): If 30x = 30, then x = 1

Part (b): if 10x + 2 = 50, then x = 24

Hypothesis: 30x = 30

Conclusion: x = 10

Supports Hypothesis: Yes

Hypothesis: 10x + 2 = 50

Conclusion: x = 24

All images/mathematical drawings were created with GeoGebra.

Hour Hand Definition < Glossary Index > Identity Definition

Rise and Sine

Conditional Statements in Geometry

Conditional statements in geometry can be confusing for even the best geometry students. The logic and proof portion of your geometry curriculum is bursting with new terminology! There are conditional statements, and the inverse, converse, contrapositive, etc. And wait, we represent them with p’s and q’s?! Ok, let’s break it down. 

What is a Conditional Statement?

A conditional statement in geometry is an “if-then” statement.

The part of the statement that follows “if” is called the hypothesis , and the part of the statement that follows “then” is called the conclusion .

We also represent conditional statements symbolically. For a conditional statement, p represents the hypothesis and q represents the conclusion. Symbolically we write p → q, which reads “if p then q.”

Statements Related to the Conditional Statement

  Inverse . To write the inverse of the conditional statement, you negate the hypothesis AND conclusion. Symbolically, it’s written as ~p → ~q and read as “If not p, then not q”.

Converse . To write the converse of the conditional statement, you switch the hypothesis and conclusion. Symbolically, it’s written as q → p and read “if q then p”.

Contrapositive . To write the contrapositive of the conditional statement, you both negate AND switch the hypothesis and conclusion. Symbolically, it’s written as ~q → ~p and read “if not q, then not p”. 

Resources for Teaching Conditional Statements

Looking for a graphic organizer to summarize conditional statements in geometry? Leave me your e-mail and I’ll send you one for FREE!  

Students can practice writing statements and determining their truth value with this self-checking assignment ! 

Stay tuned for a Logic and Proof Unit Bundle coming soon! 

Happy teaching!

Related posts

Self-Checking Math Resources: Why I Love Them and You Should Too!

Fill In The Unit Circle With This Giant Poster

10 Geometry Theorem Proofs You Need to Teach Your Students

No comments, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.