Gurumuda Networks

The first law of thermodynamics – problems and solutions
30 The first law of thermodynamics – problems and solutions
1. 3000 J of heat is added to a system and 2500 J of work is done by the system. What is the change in internal energy of the system?
Heat (Q) = +3000 Joule
Work (W) = +2500 Joule
Wanted: the change in internal energy of the system
The equation of the first law of thermodynamics
The sign conventions :
Q is positive if the heat added to the system
W is positive if work is done by the system
Q is negative if heat leaves the system
W is negative if work is done on the system
The change in internal energy of the system :
ΔU = 3000-2500
ΔU = 500 Joule
Internal energy increases by 500 Joule.
2. 2000 J of heat is added to a system and 2500 J of work is done on the system. What is the change in internal energy of the system?
Heat (Q) = +2000 Joule
Work (W) = -2500 Joule
Wanted: The change in internal energy of the system
ΔU = 2000-(-2500)
ΔU = 2000+2500
ΔU = 4500 Joule
Internal energy increases by 4500 Joule.
3. 2000 J of heat leaves the system and 2500 J of work is done on the system. What is the change in internal energy of the system?
Heat (Q) = -2000 Joule
Work (W) = -3000 Joule
ΔU = -2000-(-3000)
ΔU = -2000+3000
ΔU = 1000 Joule
Conclusion :
– If heat is added to the system, then the internal energy of the system increases
– If heat leaves the system, then the internal energy of the system decreases
– If the work is done by the system, then the internal energy of the system decreases
– If the work is done on the system, then the internal energy of the system increases
4. Calculate the change in internal energy of 2 moles of an ideal gas when 400 J of heat is added, and the gas expands, doing 300 J of work on its surroundings. Solution: Using the first law of thermodynamics: \( \Delta U = Q – W \): \[ \Delta U = 400 – 300 = 100\, \text{J} \]
5. Determine the heat transfer for a system that performs 200 J of work on its surroundings and has a change in internal energy of 50 J. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = 50 + 200 = 250\, \text{J} \]
6. Calculate the work done by a system when it absorbs 600 J of heat and its internal energy increases by 150 J. Solution: Using the first law of thermodynamics: \[ W = Q – \Delta U = 600 – 150 = 450\, \text{J} \]
7. Determine the heat transfer for a system that performs 500 J of work and its internal energy decreases by 100 J. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = (-100) + 500 = 400\, \text{J} \]
8. Calculate the change in internal energy when 300 J of heat is lost and 200 J of work is done on the system. Solution: Using the first law of thermodynamics: \[ \Delta U = -300 + 200 = -100\, \text{J} \]
9. Determine the work done on a system when it loses 400 J of heat and its internal energy decreases by 200 J. Solution: Using the first law of thermodynamics: \[ W = \Delta U – Q = (-200) – (-400) = 200\, \text{J} \]
10. Calculate the heat transfer when a system’s internal energy increases by 100 J and 50 J of work is done on the system. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = 100 + 50 = 150\, \text{J} \]
11. Determine the change in internal energy when a system absorbs 250 J of heat and performs 150 J of work on its surroundings. Solution: Using the first law of thermodynamics: \[ \Delta U = Q – W = 250 – 150 = 100\, \text{J} \]
12. Calculate the work done by the system when it loses 300 J of heat, and its internal energy decreases by 100 J. Solution: Using the first law of thermodynamics: \[ W = Q – \Delta U = -300 – (-100) = -200\, \text{J} \]
13. Determine the heat transfer for a system that does 400 J of work on its surroundings and its internal energy increases by 150 J. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = 150 + 400 = 550\, \text{J} \]
14. Calculate the change in internal energy when 500 J of heat is added, and the system does 300 J of work on its surroundings. Solution: Using the first law of thermodynamics: \[ \Delta U = Q – W = 500 – 300 = 200\, \text{J} \]
15. Determine the work done by the system when it absorbs 600 J of heat, and its internal energy increases by 200 J. Solution: Using the first law of thermodynamics: \[ W = Q – \Delta U = 600 – 200 = 400\, \text{J} \]
16. Calculate the heat transfer when a system performs 700 J of work and its internal energy decreases by 300 J. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = (-300) + 700 = 400\, \text{J} \]
17. Determine the change in internal energy when 800 J of heat is lost and 400 J of work is done on the system. Solution: Using the first law of thermodynamics: \[ \Delta U = -800 + 400 = -400\, \text{J} \]
18. Calculate the work done on the system when it loses 900 J of heat, and its internal energy decreases by 500 J. Solution: Using the first law of thermodynamics: \[ W = \Delta U – Q = (-500) – (-900) = 400\, \text{J} \]
19. Determine the heat transfer when a system’s internal energy increases by 600 J, and 300 J of work is done on the system. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = 600 + 300 = 900\, \text{J} \]
20. Calculate the change in internal energy when a system absorbs 700 J of heat and performs 350 J of work on its surroundings. Solution: Using the first law of thermodynamics: \[ \Delta U = Q – W = 700 – 350 = 350\, \text{J} \]
21. Determine the work done by the system when it loses 800 J of heat, and its internal energy decreases by 400 J. Solution: Using the first law of thermodynamics: \[ W = Q – \Delta U = -800 – (-400) = -400\, \text{J} \]
22. Calculate the heat transfer when a system does 900 J of work on its surroundings, and its internal energy increases by 450 J. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = 450 + 900 = 1350\, \text{J} \]
23. Determine the change in internal energy when 1000 J of heat is added, and the system does 500 J of work on its surroundings. Solution: Using the first law of thermodynamics: \[ \Delta U = Q – W = 1000 – 500 = 500\, \text{J} \]
24. Calculate the work done by the system when it absorbs 1100 J of heat, and its internal energy increases by 550 J. Solution: Using the first law of thermodynamics: \[ W = Q – \Delta U = 1100 – 550 = 550\, \text{J} \]
25. Determine the heat transfer when a system performs 1200 J of work, and its internal energy decreases by 600 J. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = (-600) + 1200 = 600\, \text{J} \]
26. Calculate the change in internal energy when 1300 J of heat is lost, and 650 J of work is done on the system. Solution: Using the first law of thermodynamics: \[ \Delta U = -1300 + 650 = -650\, \text{J} \]
27. Determine the work done on the system when it loses 1400 J of heat, and its internal energy decreases by 700 J. Solution: Using the first law of thermodynamics: \[ W = \Delta U – Q = (-700) – (-1400) = 700\, \text{J} \]
28. Calculate the heat transfer when a system’s internal energy increases by 800 J, and 400 J of work is done on the system. Solution: Using the first law of thermodynamics: \[ Q = \Delta U + W = 800 + 400 = 1200\, \text{J} \]
29. Determine the change in internal energy when a system absorbs 1500 J of heat and performs 750 J of work on its surroundings. Solution: Using the first law of thermodynamics: \[ \Delta U = Q – W = 1500 – 750 = 750\, \text{J} \]
30. Calculate the work done by the system when it loses 1600 J of heat, and its internal energy decreases by 800 J. Solution: Using the first law of thermodynamics: \[ W = Q – \Delta U = -1600 – (-800) = -800\, \text{J} \]
These problems and solutions are designed to provide a comprehensive understanding of the first law of thermodynamics, which states that the change in internal energy of a closed system is equal to the heat added to the system minus the work done by the system.

Share this:
About me and why I created this physics website.
Thermodynamics Problems
- Search Website
Real World Applications — for high school level and above
- Amusement Parks
- Battle & Weapons
- Engineering
- Miscellaneous
Education & Theory — for high school level and above
- Useful Formulas
- Physics Questions
- Example Mechanics Problems
- Learn Physics Compendium
Kids Section
- Physics For Kids
- Science Experiments
- Science Fair Ideas
- Science Quiz
- Science Toys
- Teacher Resources
- Commercial Disclosure
- Privacy Policy
© Copyright 2009-2024 real-world-physics-problems.com
Subjects Home
- Privacy Policy
Read Chemistry
The first law of thermodynamics + solved problems.
Read Chemistry May 21, 2019 Physical Chemistry
– The first law of Thermodynamics states that The total energy of an isolated system remains constant though it may change from one form to another.
Internal Energy
– A thermodynamic system containing some quantity of matter has within itself a definite quantity of energy.
– This energy includes not only the translation kinetic energy of the molecules but also other molecular energies such as rotational, and vibrational energies.
– The kinetic and potential energy of the nuclei and electrons within the individual molecules also contribute to the energy of the system.
– Internal Energy is The total of all the possible kinds of energy of a system.
– The word (internal) is often omitted and the energy of a system always implies internal energy.
– The internal energy of a system, like temperature, pressure, volume, etc., is determined by the state of a system and is independent of the path by which it is obtained.
– Hence internal energy of a system is a state function.
– For example, we consider the heating of one mole of liquid water from 0 º to 100 º C.
– The change in energy is 1.8 kcal and is the same regardless of the form in which this energy is transferred to the water by heating, by performing work, by electrical means, or in any other way.
– Since the value of the internal energy of a system depends on the mass of the matter contained in a system, it is classed as an extensive property.
Symbol Representation of Internal Energy and Sign Conventions
– The internal energy of a system is represented by the symbol (E) (Some books use the symbol U).
– It is neither possible nor necessary to calculate the absolute value of the internal energy of a system.
– In thermodynamics, we are concerned only with the energy changes when a system changes from one state to another.
– If ΔE is the difference in energy of the initial state (E in ) and the final state (E f ), we can write
ΔE = E f – E in
ΔE is +ve if E f is greater than E in
and ΔE is –ve if E f is less than E in .
– A system may transfer energy to or from the surroundings as heat or as work, or both.
Units of Internal Energy
– The SI unit for the internal energy of a system is the joule (J).
– Another unit of energy that is not an SI unit is the calorie, 1 cal = 4.184 J.
The first law of Thermodynamics statement
– The first law of thermodynamics is, in fact, an application of the broad principle known as the Law of Conservation of Energy to the thermodynamic system.
– First law of Thermodynamics states that: The total energy of an isolated system remains constant though it may change from one form to another.
– When a system is changed from state A to state B, it undergoes a change in the internal energy from E A to E B .
– Thus, we can write:
ΔE = E B – E A
– This energy change is brought about by the evolution or absorption of heat and/or by work being done by the system.
– Because the total energy of the system must remain constant, we can write the mathematical statement of the First Law as:
ΔE = q – w …(1)
– where q = the amount of heat supplied to the system, w = work done by the system
– Thus the First Law may also be stated as the net energy change of a closed system is equal to the heat transferred to the system minus the work done by the system.
– To illustrate the mathematical statement of the First Law, let us consider the system ‘expanding hot gas’.
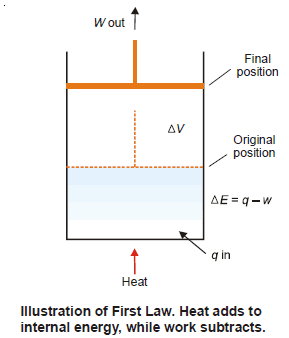
– The gas expands against an applied constant pressure by volume ΔV.
– The total mechanical work done is given by the relation:
w = P × ΔV …(2)
– From (1) and (2), we can restate:
ΔE = q – P × ΔV

Other Definitions of the First Law of Thermodynamics
(1) Whenever energy of a particular type disappears equivalent amount of another type must be produced.
(2) Total energy of a system and surroundings remains constant (or conserved)
(3) It is impossible to construct a perpetual motion machine that can produce work without spending energy on it.
Some Special Forms of the First Law of Thermodynamics
– The mathematical statement of the First Law of Thermodynamics is:
Case (1): For a cyclic process involving isothermal expansion of an ideal gas
Case (2): For an isochoric process (no change in volume) there is no work of expansion i.e. w = 0.
Case (3): For an adiabatic process there is no change in heat gained or lost i.e. q = 0.
– In other words, the decrease in internal energy is exactly equal to the work done on the system by surroundings.
Case (4): For an isobaric process there is no change in pressure, i.e. P remains constant.
or ΔE = q – PΔV
Solved Problem
Problem (1): Find ΔE, q, and w if 2 moles of hydrogen at 3 atm pressure expand isothermally at 50ºC and reversibly to a pressure of 1 atm.
– Since the operation is isothermal and the gas is ideal

Problem (2): 1g of water at 373 K is converted into steam at the same temperature. The volume of water becomes 1671 ml on boiling. Calculate the change in the internal energy of the system if the heat of vaporization is 540 cal/g.
– As the vaporization takes place against a constant pressure of 1 atmosphere, work done for an irreversible process, w, is:
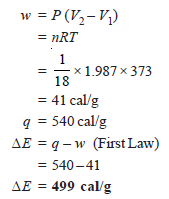
Problem (3): A gas contained in a cylinder fitted with a frictionless piston expands against a constant external pressure of 1 atm from a volume of 5 liters to a volume of 10 liters. In doing so it absorbs 400 J thermal energy from its surroundings. Determine ΔE for the process.
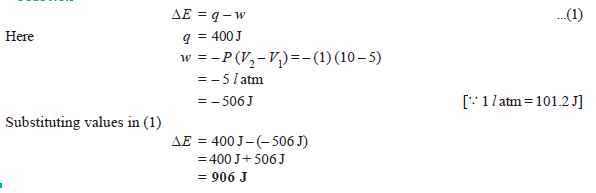
Problem (4): Calculate the maximum work done when pressure on 10 g of hydrogen is reduced from 20 to one atmosphere at a constant temperature of 273 K. The gas behaves ideally. Will there be any change in internal energy? Also, calculate ‘q’.
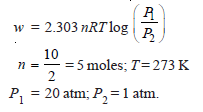
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.
Related posts:
- Heat of Formation (Definition, Applications, Solved Problems)
- Types of Radiations and its properties
- Difference between Isotopes, Isobar, and Isotones
- Ways of Expressing Concentration
- Laws of Osmotic Pressure
- What is meant by A phase and components?
- Sulphur system – Phase diagram of Sulphur
- How to determine the order of reaction?
- Gels : Defination, Types, Properties
Macromolecules : Definition and Molecular Weight
Related articles.

Gibbs Helmholtz Equations
October 20, 2024
Carnot Cycle – Definition, Theorem, Efficiency, Derivation
May 22, 2024
Entropy : Definition, Units, Solved Problems
May 21, 2024
May 20, 2024

Second Law of Thermodynamics: MCQ Quiz with answers
May 18, 2024
Applications of Colloids
Leave a reply cancel reply.
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.

- Exam Center
- Ticket Center
- Flash Cards
- Heat and Thermal Physics
Heat Practice Problems With Detailed Answers
Struggling with heat problems in your physics class?
Our article is here to help! Packed with solved examples specifically designed for high school students, this guide will make mastering heat problems easy.
Get ready to boost your grades and deepen your understanding with these easy-to-follow solutions!
When heat energy $Q$ causes a change in temperature $\Delta T=T_f-T_i$ in a sample with specific heat capacity $c$ and mass $m$, then we can relate all these physical quantities as following formula \[Q=mc\Delta T=mc(T_f-T_i)\] where $T_f$ and $T_i$ are the initial and final temperatures.
Heat Practice Problems
Problem (1): 5.0 g of copper was heated from 20°C to 80°C. How much energy was used to heat Cu? (Specific heat capacity of Cu is 0.092 cal/g. °C)
Solution : The energy required to change the temperature of a substance of mass $m$ from initial temperature $T_i$ to final temperature $T_f$ is obtained by the formula $Q=mc(T_f-T_i)$, where $c$ is the specific heat of the substance. Thus, we have \begin{align*} Q&=mc\Delta T\\ &= 5\times 0.092\times (80^\circ-20^\circ)\\&= 27.6 \quad {\rm cal} \end{align*} So, it would require 27.6 calories of heat energy to increase the temperature of this substance from 20°C to 80°C.
If this page helped you with homework or anything else, please support me here .
Problem (2): How much heat is absorbed by a 20 g granite boulder as energy from the sun causes its temperature to change from 10°C to 29°C? (Specific heat capacity of granite is 0.1 cal/g.°C)
Solution : to raise the temperature of the granite boulder from 10°C to 29°C, we must add $Q=mc\Delta T$ energy to the granite as below \begin{align*} Q&=mc\Delta T\\ &=20 \times 0.1\times (29^\circ-10^\circ)\\&=38\quad {\rm cal}\end{align*} So, it would require 38 calories of heat energy to increase the temperature of this granite boulder from 10°C to 29°C. This is the amount of energy we must add to the boulder.
In all these example problems, there is no change in the state of the substance. If there were a change in the phase of matter (solid $\Leftrightarrow$ liquid or to liquid$\Leftrightarrow$ gas) read the following page to learn more:
Solved problems on latent heat of fusion
Solved Problems on latent heat of vaporization
Problem (3): How much heat is released when 30 g of water at 96°C cools to 25°C? The specific heat of water is 1 cal/g.°C.
Solution : the amount of energy released is obtained by formula $Q=mc\Delta T$ as below \begin{align*} Q&=mc\Delta T\\&=30\times 1\times (25^\circ-96^\circ)\\&= -2130\quad {\rm cal}\end{align*} The negative sign in the result indicates that the energy is being released from the water. This is because the temperature of the water is decreasing, which means it is losing heat energy.
Therefore, $2130$ calories of heat energy are released from the water when its temperature decreases from 96°C to 25°C. This energy could be transferred to the surrounding environment or used to do work, depending on the specific circumstances.
Were these not helpful? My income comes from your generous donations. Please support me.
Problem (4): If a 3.1 g ring is heated using 10.0 calories, its temperature rises 17.9°C. Calculate the specific heat capacity of the ring.
Solution : Since the given heat causes a change in the temperature of the ring, the amount of heat is obtained by the formula $Q=mc(T_f-T_i)$. By putting known values into it and solving for the unknown value, the specific heat of the ring is calculated as below, \begin{align*} c&=\frac{Q}{m(T_f-T_i)}\\ \\ &=\frac{10}{3.1\times 17.9^\circ}\\ \\&=0.18\quad {\rm cal/g\cdot ^\circ C}\end{align*} So, the specific heat of the ring is calculated to be $0.18\,{\rm cal/g\cdot ^\circ C}$. This value tells us how much heat is required to raise the temperature of $1$ gram of the ring by $1$ degree Celsius. Note that in this problem, the difference between temperatures is not the initial or final temperatures.
Problem (5): The temperature of a sample of water increases from 20°C to 46.6°C as it absorbs 5650 calories of heat. What is the mass of the sample? (Specific heat of water is 1.0 cal/g.°C)
Solution : As before, using heat formula and solving for mass $m$, we get \begin{align*} m&=\frac{Q}{c\Delta T}\\\\ &=\frac{5650}{1\times (46.6^\circ-20^\circ)}\\ \\&=212.4\quad {\rm g}\end{align*}
Problem (6): The temperature of a sample of iron with a mass of 10.0 g changed from 50.4°C to 25.0°C with the release of 47 calories of heat. What is the specific heat of iron?
Solution : In the specific heat problems , we learned that the specific heat is defined as the amount of heat energy required to change the temperature of a sample with mass $m$ by $\Delta T$.
Here, energy is released by as much as 47 calories, so we must put it with a negative sign into the equation. Thus, we have \begin{align*} c&=\frac{Q}{m\Delta T}\\ \\&=\frac{-47}{10\times (25^\circ-50.4^\circ)}\\ \\&= 0.185\quad {\rm cal/g\cdot ^\circ \! C}\end{align*}
Problem (7): A 4.50 g coin of copper absorbed 54 calories of heat. What was the final temperature of the copper if the initial temperature was 25°C? The specific heat of copper is 0.092 cal/g.°C.
Solution : Let $T_i$ and $T_f$ be the initial and final temperatures of the copper coin. Again using formula $Q=mc(T_f-T_i)$ and solving for final temperature $T_f$, we have \begin{align*} T_f&=\frac{Q}{mc}+T_i \\ \\ &=\frac{54}{0.092\times 4.5}+25^\circ\\ \\ &=155.43\,{\rm ^\circ C}\end{align*}
Problem (8): A 155 g sample of an unknown substance was heated from 25°C to 40°C. In the process, the substance absorbed 569 calories of energy. What is the specific heat of the substance?
Solution : In the heat formula $Q=mc\Delta T$, the specific heat of any substance is denoted by $c$. Putting known values into this formula and solving for unknown specific heat, we get \begin{align*} c&=\frac{Q}{m\Delta T}\\ \\ &=\frac{569}{155\times (40^\circ-25^\circ)}\\ \\&=0.244\quad {\rm cal/g\cdot^\circ\! C} \end{align*}
Problem (9): What is the specific heat of an unknown substance if a 2.50 g sample releases 12 calories as its temperature changes from 25°C to 20°C?
Solution : same as above, we have \begin{align*} c&=\frac{Q}{m(T_f-T_i)}\\ \\&=\frac{12}{2.5\times (20^\circ-25^\circ)}\\\\&=0.96\quad {\rm cal/g\cdot ^\circ \! C}\end{align*}
Problem (10): When 3 kg of water is cooled from 80°C to 10°C, how much heat energy is lost? (specific heat of water is $c_W=4.179\,{\rm J/g\cdot ^\circ C}$)
Solution : the heat has led to a change in temperature, so we must use the formula $Q=mc\Delta T$ to find the lost heat as shown below: \begin{align*} Q&=mc(T_f-T_i)\\&=3000\times 4.179\times (10^\circ-80^\circ)\\&=-877590\quad {\rm J} \\ or &=-877.590\quad {\rm kJ}\end{align*} Note that in the above calculation, the value of specific heat is given in grams, and the weight of water is in kilograms. Therefore, first convert them into grams or kilograms and then continue to solve the problem. Here, we converted 3 kg to 3000 g.
The negative sign indicates that the heat is released from the water.
Problem (11): How much heat is needed to raise a 0.30 kg piece of aluminum from 30°C to 150°C? ($c_{Al}=0.9\,{\rm J/g\cdot ^\circ C}$)
Solution: Let $T_f$ and $T_i$ be the initial and final temperatures of the aluminum so the required heat is computed as below \begin{align*} Q&=mc(T_f-T_i)\\&=0.3\times 900\times (150^\circ-30^\circ)\\&=-32400\quad {\rm J}\\ or &=-32.4\quad {\rm kJ}\end{align*} Here, we converted specific heat in SI units.
Problem (12): Calculate the temperature change when: (a) 10.0 kg of water loses 232 kJ of heat. ($c_W=4.179\,{\rm J/g\cdot ^\circ C}$) (b) 1.96 kJ of heat is added to 500 g of copper.($c_{Cu}=0.385\,{\rm J/g\cdot ^\circ C}$)
Solution : In both parts, we use the heat formula when temperature changes, $Q=mc(T_f-T_i)$. (a) Substituting known values $m=10\,{\rm kg}$ and $Q=232\,{\rm kJ}$ into the above equation and solving for the change in temperature $\Delta T=T_f-T_i$, we get: \begin{align*} \Delta T&= \frac{Q}{mc}\\ \\&=\frac{-232000}{10\times 4179}\\ \\&=-5.55\,{\rm ^\circ C}\end{align*} Since water loses heat energy (which justifies why we inserted a minus sign for Q), its temperature must be decreasing. In the above, kJ means 1000 J of energy.
(b) Heat is added to the water, so $Q>0$ must be inserted into the formula, \begin{align*}\Delta T&=\frac{Q}{mc}\\ \\&=\frac{1960}{0.5\times 385}\\ \\&=10.18\,{\rm ^\circ C}\end{align*}
Problem (13): When heated, the temperature of a water sample increased from 15°C to 39°C. It absorbed 4300 joules of heat. What is the mass of the sample?
Solution : putting known values into the equation $Q=mc(T_f-T_i)$ and solving for unknown mass, we get \begin{align*} m&=\frac{Q}{c(T_f-T_i)}\\ \\ &=\frac{4300}{4179\times (15^\circ-39^\circ)}\\ \\&=0.0428\quad {\rm kg}\\ \\ or &=42.8\quad {\rm g} \end{align*}
Problem (14): 5.0 g of copper was heated from 20°C to 80°C. How much energy was used to heat Cu?
Solution : the necessary energy is calculated as below: \begin{align*} Q&=mc(T_f-T_i)\\&=5\times 0.385\times (20^\circ-80^\circ)\\&=115.5\quad {\rm J}\end{align*} So, the necessary energy or heat absorbed by the object is calculated to be $\rm 115.5\, J$. This value tells us how much heat energy is required to change the temperature of the $\rm 5\, g$ object by $60$ degrees Celsius.
Problem (15): The temperature of a sample of water increases from 20°C to 46.6°C as it absorbs 5650 Joules of heat. What is the mass of the sample?
Solution : known values are $T_i={\rm 20^\circ C}$, $T_f={\rm 46.6^\circ C}$ and $Q=5650\,{\rm J}$. We can rearrange the formula to solve for ($m$): \begin{align*} m&=\frac{Q}{c(T_f-T_i)}\\ \\&=\frac{5650}{4179\times (46.6^\circ-20^\circ)}\\ \\ &=0.0508\quad {\rm kg} \\ \\ or &=50.8\quad {\rm g} \end{align*} So, the mass of the water sample is approximately ($50.7$) grams.
Author : Dr. Ali Nemati Page Created: 3/9/2021
© 2015 All rights reserved. by Physexams.com

IMAGES
VIDEO
COMMENTS
Title: Topic VIII - Page 6 Author: Gregg Wagener Created Date: 6/4/2001 12:10:18 PM
Question 1. What is true of Isothermal Process (a) ΔT >0 (b) ΔU=0 (c) ΔQ=ΔW (d) PV=constants Solution In an Isothermal Process Temperature remains constant ΔT =0 Since Internal energy depends on the temperature ΔU=0 From first law of Thermodynamics ΔU=ΔQ-ΔW Since ΔU=0 ΔQ=ΔW Also PV=nRT As T is constant PV= constant Question 2 Two absolute scales A and B have triple points of water ...
Thermodynamics - problems and solutions. The first law of thermodynamics. 1. Based on graph P-V below, what is the ratio of the work done by the gas in the process I, to the work done by the gas in the process II? Known : Process 1 : Pressure (P) = 20 N/m 2. Initial volume (V 1) = 10 liter = 10 dm 3 = 10 x 10-3 m 3.
14. Calculate the change in internal energy when 500 J of heat is added, and the system does 300 J of work on its surroundings. Solution: Using the first law of thermodynamics: \[\Delta U = Q - W = 500 - 300 = 200\, \text{J} \] 15. Determine the work done by the system when it absorbs 600 J of heat, and its internal energy increases by 200 J. Solution: Using the first law of thermodynamics ...
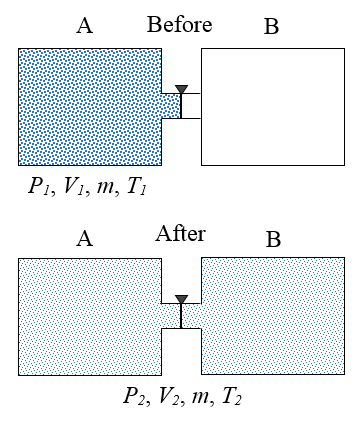
See answer Answers For Thermodynamics Problems Answer for Problem # 1 Since the containers are insulated, no heat transfer occurs between the gas and the external environment, and since the gas expands freely into container B there is no resistance "pushing" against it, which means no work is done on the gas as it expands. As a result, the ...
subjects home. contents chapter previous next prep find. contents: thermodynamics chapter 01: thermodynamic properties and state of pure. substances. chapter 02: work and heat. chapter 03: energy and the first law of thermodynamics. chapter 04: entropy and the second law of thermodynamics. chapter 05: irreversibility and availability
Some Special Forms of the First Law of Thermodynamics - The mathematical statement of the First Law of Thermodynamics is: ΔE = q - w. Case (1): For a cyclic process involving isothermal expansion of an ideal gas. ΔE = o. ∴ q = w. Case (2): For an isochoric process (no change in volume) there is no work of expansion i.e. w = 0. Hence ...
When solving a Physics problem in general and one of Thermodynamics in particular, it is important to follow a certain order. Get used to being organized when you solve problems, and you will see how it gives good results. It is worth spending a little time on the previous analysis of a problem before you tackle it.
The process of solving thermodynamics problems was outlined, emphasizing the identification of the problem, application of appropriate thermodynamic laws and equations, and the importance of checking the solutions for consistency. Two practical examples were provided to illustrate the concepts. Finally, common mistakes and challenges were ...
This value tells us how much heat is required to raise the temperature of $1$ gram of the ring by $1$ degree Celsius. Note that in this problem, the difference between temperatures is not the initial or final temperatures. Problem (5): The temperature of a sample of water increases from 20°C to 46.6°C as it absorbs 5650 calories of heat.