what is variable presentation

Home Blog Design Understanding Data Presentations (Guide + Examples)

Understanding Data Presentations (Guide + Examples)

In this age of overwhelming information, the skill to effectively convey data has become extremely valuable. Initiating a discussion on data presentation types involves thoughtful consideration of the nature of your data and the message you aim to convey. Different types of visualizations serve distinct purposes. Whether you’re dealing with how to develop a report or simply trying to communicate complex information, how you present data influences how well your audience understands and engages with it. This extensive guide leads you through the different ways of data presentation.

Table of Contents

What is a Data Presentation?

What should a data presentation include, line graphs, treemap chart, scatter plot, how to choose a data presentation type, recommended data presentation templates, common mistakes done in data presentation.

A data presentation is a slide deck that aims to disclose quantitative information to an audience through the use of visual formats and narrative techniques derived from data analysis, making complex data understandable and actionable. This process requires a series of tools, such as charts, graphs, tables, infographics, dashboards, and so on, supported by concise textual explanations to improve understanding and boost retention rate.

Data presentations require us to cull data in a format that allows the presenter to highlight trends, patterns, and insights so that the audience can act upon the shared information. In a few words, the goal of data presentations is to enable viewers to grasp complicated concepts or trends quickly, facilitating informed decision-making or deeper analysis.

Data presentations go beyond the mere usage of graphical elements. Seasoned presenters encompass visuals with the art of data storytelling , so the speech skillfully connects the points through a narrative that resonates with the audience. Depending on the purpose – inspire, persuade, inform, support decision-making processes, etc. – is the data presentation format that is better suited to help us in this journey.

To nail your upcoming data presentation, ensure to count with the following elements:

• Clear Objectives: Understand the intent of your presentation before selecting the graphical layout and metaphors to make content easier to grasp.
• Engaging introduction: Use a powerful hook from the get-go. For instance, you can ask a big question or present a problem that your data will answer. Take a look at our guide on how to start a presentation for tips & insights.
• Structured Narrative: Your data presentation must tell a coherent story. This means a beginning where you present the context, a middle section in which you present the data, and an ending that uses a call-to-action. Check our guide on presentation structure for further information.
• Visual Elements: These are the charts, graphs, and other elements of visual communication we ought to use to present data. This article will cover one by one the different types of data representation methods we can use, and provide further guidance on choosing between them.
• Insights and Analysis: This is not just showcasing a graph and letting people get an idea about it. A proper data presentation includes the interpretation of that data, the reason why it’s included, and why it matters to your research.
• Conclusion & CTA: Ending your presentation with a call to action is necessary. Whether you intend to wow your audience into acquiring your services, inspire them to change the world, or whatever the purpose of your presentation, there must be a stage in which you convey all that you shared and show the path to staying in touch. Plan ahead whether you want to use a thank-you slide, a video presentation, or which method is apt and tailored to the kind of presentation you deliver.
• Q&A Session: After your speech is concluded, allocate 3-5 minutes for the audience to raise any questions about the information you disclosed. This is an extra chance to establish your authority on the topic. Check our guide on questions and answer sessions in presentations here.

Bar charts are a graphical representation of data using rectangular bars to show quantities or frequencies in an established category. They make it easy for readers to spot patterns or trends. Bar charts can be horizontal or vertical, although the vertical format is commonly known as a column chart. They display categorical, discrete, or continuous variables grouped in class intervals [1] . They include an axis and a set of labeled bars horizontally or vertically. These bars represent the frequencies of variable values or the values themselves. Numbers on the y-axis of a vertical bar chart or the x-axis of a horizontal bar chart are called the scale.

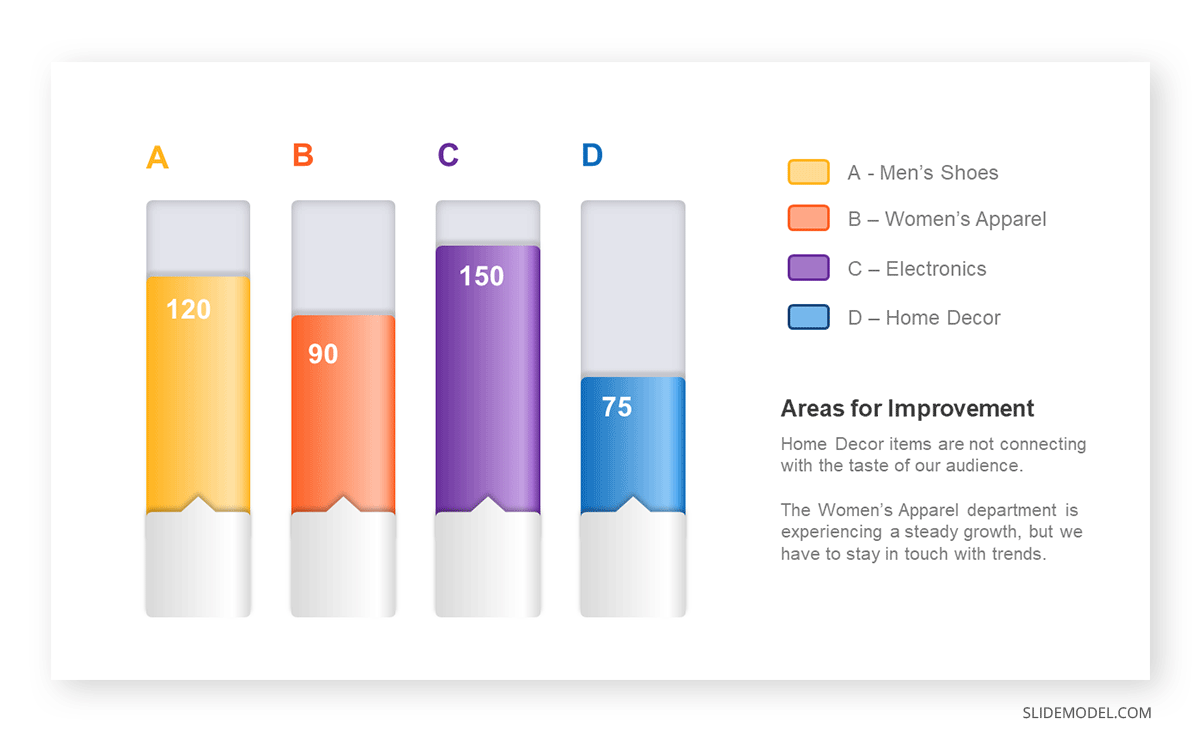
Real-Life Application of Bar Charts

Let’s say a sales manager is presenting sales to their audience. Using a bar chart, he follows these steps.

Step 1: Selecting Data

The first step is to identify the specific data you will present to your audience.

The sales manager has highlighted these products for the presentation.

• Product A: Men’s Shoes
• Product B: Women’s Apparel
• Product C: Electronics
• Product D: Home Decor

Step 2: Choosing Orientation

Opt for a vertical layout for simplicity. Vertical bar charts help compare different categories in case there are not too many categories [1] . They can also help show different trends. A vertical bar chart is used where each bar represents one of the four chosen products. After plotting the data, it is seen that the height of each bar directly represents the sales performance of the respective product.

It is visible that the tallest bar (Electronics – Product C) is showing the highest sales. However, the shorter bars (Women’s Apparel – Product B and Home Decor – Product D) need attention. It indicates areas that require further analysis or strategies for improvement.

Step 3: Colorful Insights

Different colors are used to differentiate each product. It is essential to show a color-coded chart where the audience can distinguish between products.

• Men’s Shoes (Product A): Yellow
• Women’s Apparel (Product B): Orange
• Electronics (Product C): Violet
• Home Decor (Product D): Blue

Bar charts are straightforward and easily understandable for presenting data. They are versatile when comparing products or any categorical data [2] . Bar charts adapt seamlessly to retail scenarios. Despite that, bar charts have a few shortcomings. They cannot illustrate data trends over time. Besides, overloading the chart with numerous products can lead to visual clutter, diminishing its effectiveness.

For more information, check our collection of bar chart templates for PowerPoint .

Line graphs help illustrate data trends, progressions, or fluctuations by connecting a series of data points called ‘markers’ with straight line segments. This provides a straightforward representation of how values change [5] . Their versatility makes them invaluable for scenarios requiring a visual understanding of continuous data. In addition, line graphs are also useful for comparing multiple datasets over the same timeline. Using multiple line graphs allows us to compare more than one data set. They simplify complex information so the audience can quickly grasp the ups and downs of values. From tracking stock prices to analyzing experimental results, you can use line graphs to show how data changes over a continuous timeline. They show trends with simplicity and clarity.

Real-life Application of Line Graphs

To understand line graphs thoroughly, we will use a real case. Imagine you’re a financial analyst presenting a tech company’s monthly sales for a licensed product over the past year. Investors want insights into sales behavior by month, how market trends may have influenced sales performance and reception to the new pricing strategy. To present data via a line graph, you will complete these steps.

First, you need to gather the data. In this case, your data will be the sales numbers. For example:

• January: $45,000
• February: $55,000
• March: $45,000
• April: $60,000
• May: $ 70,000
• June: $65,000
• July: $62,000
• August: $68,000
• September: $81,000
• October: $76,000
• November: $87,000
• December: $91,000

After choosing the data, the next step is to select the orientation. Like bar charts, you can use vertical or horizontal line graphs. However, we want to keep this simple, so we will keep the timeline (x-axis) horizontal while the sales numbers (y-axis) vertical.

Step 3: Connecting Trends

After adding the data to your preferred software, you will plot a line graph. In the graph, each month’s sales are represented by data points connected by a line.

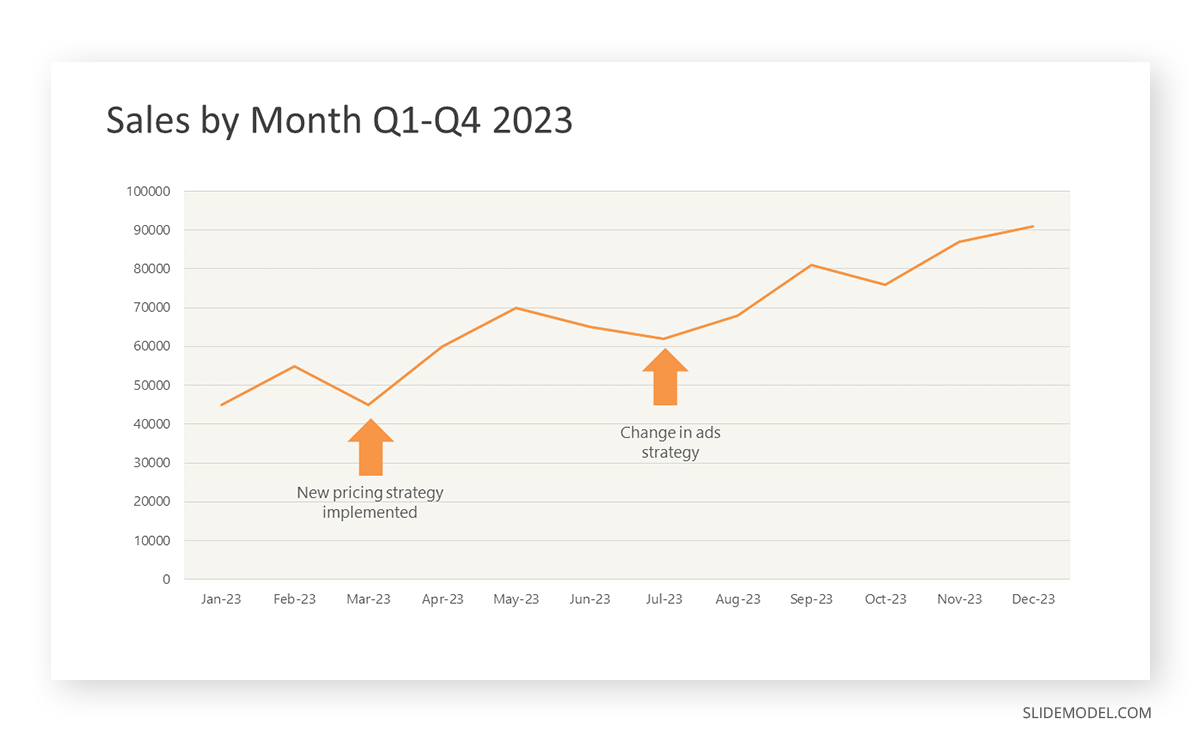
Step 4: Adding Clarity with Color

If there are multiple lines, you can also add colors to highlight each one, making it easier to follow.

Line graphs excel at visually presenting trends over time. These presentation aids identify patterns, like upward or downward trends. However, too many data points can clutter the graph, making it harder to interpret. Line graphs work best with continuous data but are not suitable for categories.

For more information, check our collection of line chart templates for PowerPoint and our article about how to make a presentation graph .

A data dashboard is a visual tool for analyzing information. Different graphs, charts, and tables are consolidated in a layout to showcase the information required to achieve one or more objectives. Dashboards help quickly see Key Performance Indicators (KPIs). You don’t make new visuals in the dashboard; instead, you use it to display visuals you’ve already made in worksheets [3] .

Keeping the number of visuals on a dashboard to three or four is recommended. Adding too many can make it hard to see the main points [4]. Dashboards can be used for business analytics to analyze sales, revenue, and marketing metrics at a time. They are also used in the manufacturing industry, as they allow users to grasp the entire production scenario at the moment while tracking the core KPIs for each line.

Real-Life Application of a Dashboard

Consider a project manager presenting a software development project’s progress to a tech company’s leadership team. He follows the following steps.

Step 1: Defining Key Metrics

To effectively communicate the project’s status, identify key metrics such as completion status, budget, and bug resolution rates. Then, choose measurable metrics aligned with project objectives.

Step 2: Choosing Visualization Widgets

After finalizing the data, presentation aids that align with each metric are selected. For this project, the project manager chooses a progress bar for the completion status and uses bar charts for budget allocation. Likewise, he implements line charts for bug resolution rates.

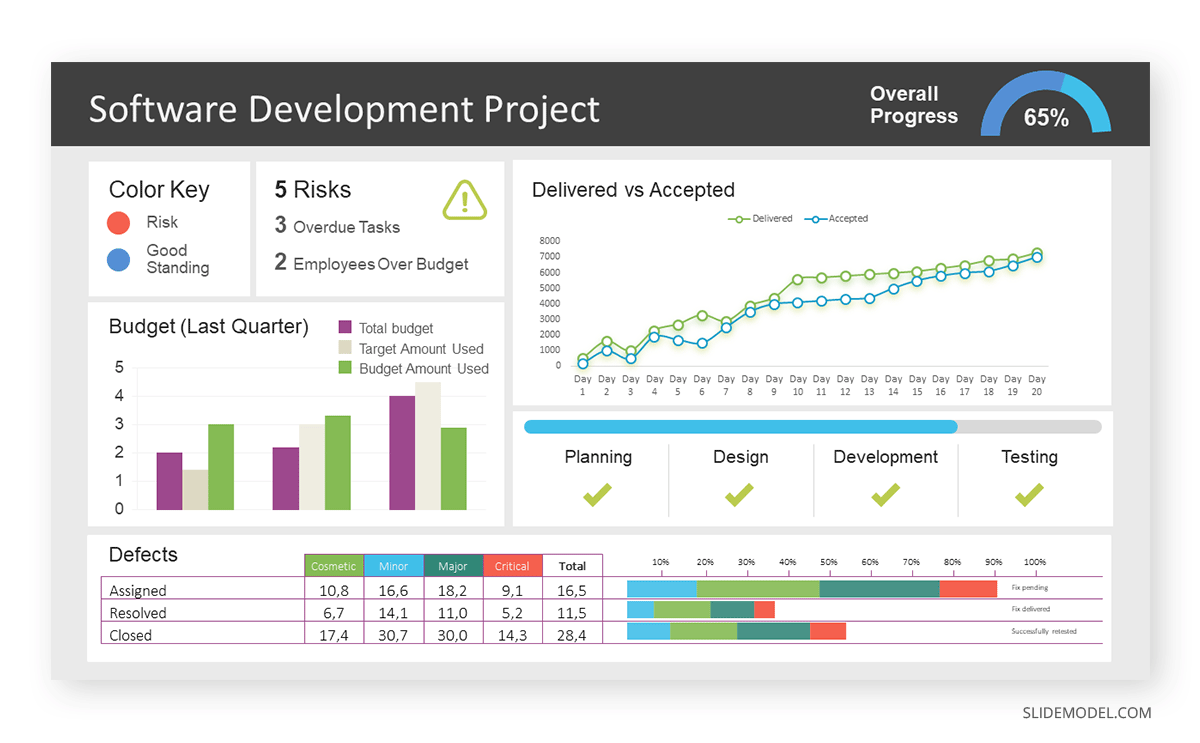
Step 3: Dashboard Layout

Key metrics are prominently placed in the dashboard for easy visibility, and the manager ensures that it appears clean and organized.

Dashboards provide a comprehensive view of key project metrics. Users can interact with data, customize views, and drill down for detailed analysis. However, creating an effective dashboard requires careful planning to avoid clutter. Besides, dashboards rely on the availability and accuracy of underlying data sources.

For more information, check our article on how to design a dashboard presentation , and discover our collection of dashboard PowerPoint templates .

Treemap charts represent hierarchical data structured in a series of nested rectangles [6] . As each branch of the ‘tree’ is given a rectangle, smaller tiles can be seen representing sub-branches, meaning elements on a lower hierarchical level than the parent rectangle. Each one of those rectangular nodes is built by representing an area proportional to the specified data dimension.

Treemaps are useful for visualizing large datasets in compact space. It is easy to identify patterns, such as which categories are dominant. Common applications of the treemap chart are seen in the IT industry, such as resource allocation, disk space management, website analytics, etc. Also, they can be used in multiple industries like healthcare data analysis, market share across different product categories, or even in finance to visualize portfolios.

Real-Life Application of a Treemap Chart

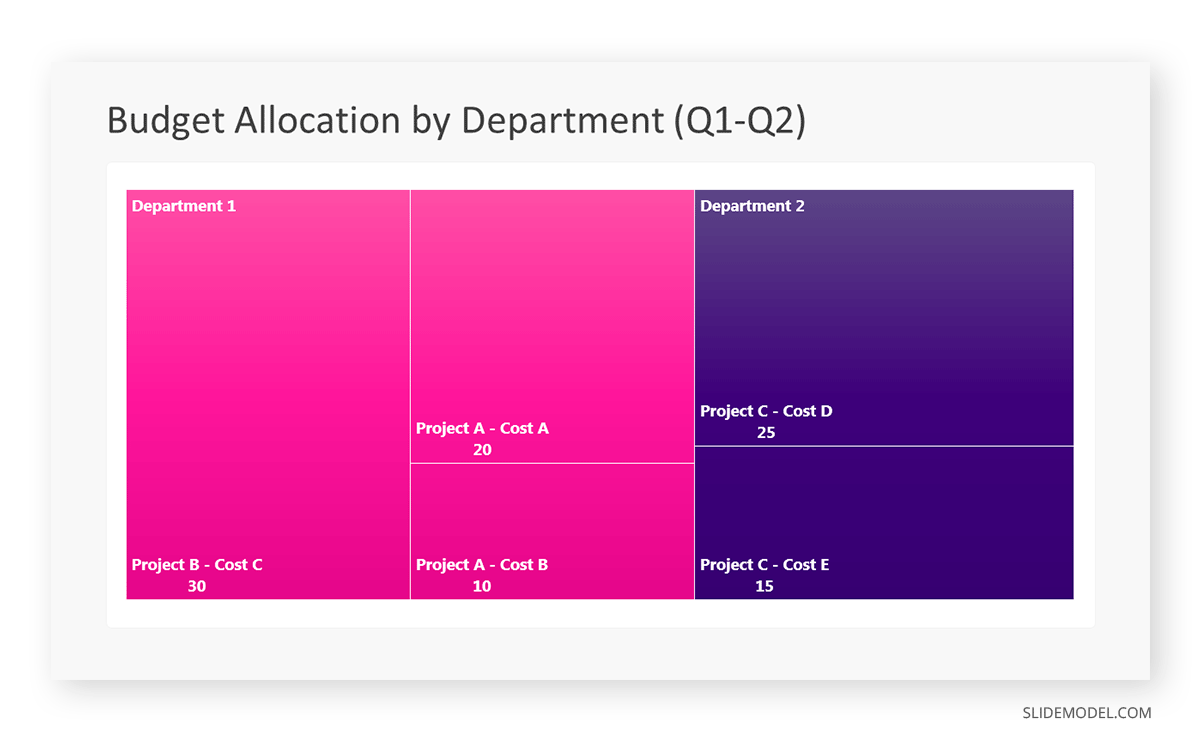
Let’s consider a financial scenario where a financial team wants to represent the budget allocation of a company. There is a hierarchy in the process, so it is helpful to use a treemap chart. In the chart, the top-level rectangle could represent the total budget, and it would be subdivided into smaller rectangles, each denoting a specific department. Further subdivisions within these smaller rectangles might represent individual projects or cost categories.

Step 1: Define Your Data Hierarchy

While presenting data on the budget allocation, start by outlining the hierarchical structure. The sequence will be like the overall budget at the top, followed by departments, projects within each department, and finally, individual cost categories for each project.

• Top-level rectangle: Total Budget
• Second-level rectangles: Departments (Engineering, Marketing, Sales)
• Third-level rectangles: Projects within each department
• Fourth-level rectangles: Cost categories for each project (Personnel, Marketing Expenses, Equipment)

Step 2: Choose a Suitable Tool

It’s time to select a data visualization tool supporting Treemaps. Popular choices include Tableau, Microsoft Power BI, PowerPoint, or even coding with libraries like D3.js. It is vital to ensure that the chosen tool provides customization options for colors, labels, and hierarchical structures.

Here, the team uses PowerPoint for this guide because of its user-friendly interface and robust Treemap capabilities.

Step 3: Make a Treemap Chart with PowerPoint

After opening the PowerPoint presentation, they chose “SmartArt” to form the chart. The SmartArt Graphic window has a “Hierarchy” category on the left.  Here, you will see multiple options. You can choose any layout that resembles a Treemap. The “Table Hierarchy” or “Organization Chart” options can be adapted. The team selects the Table Hierarchy as it looks close to a Treemap.

Step 5: Input Your Data

After that, a new window will open with a basic structure. They add the data one by one by clicking on the text boxes. They start with the top-level rectangle, representing the total budget.  

Step 6: Customize the Treemap

By clicking on each shape, they customize its color, size, and label. At the same time, they can adjust the font size, style, and color of labels by using the options in the “Format” tab in PowerPoint. Using different colors for each level enhances the visual difference.

Treemaps excel at illustrating hierarchical structures. These charts make it easy to understand relationships and dependencies. They efficiently use space, compactly displaying a large amount of data, reducing the need for excessive scrolling or navigation. Additionally, using colors enhances the understanding of data by representing different variables or categories.

In some cases, treemaps might become complex, especially with deep hierarchies.  It becomes challenging for some users to interpret the chart. At the same time, displaying detailed information within each rectangle might be constrained by space. It potentially limits the amount of data that can be shown clearly. Without proper labeling and color coding, there’s a risk of misinterpretation.

A heatmap is a data visualization tool that uses color coding to represent values across a two-dimensional surface. In these, colors replace numbers to indicate the magnitude of each cell. This color-shaded matrix display is valuable for summarizing and understanding data sets with a glance [7] . The intensity of the color corresponds to the value it represents, making it easy to identify patterns, trends, and variations in the data.

As a tool, heatmaps help businesses analyze website interactions, revealing user behavior patterns and preferences to enhance overall user experience. In addition, companies use heatmaps to assess content engagement, identifying popular sections and areas of improvement for more effective communication. They excel at highlighting patterns and trends in large datasets, making it easy to identify areas of interest.

We can implement heatmaps to express multiple data types, such as numerical values, percentages, or even categorical data. Heatmaps help us easily spot areas with lots of activity, making them helpful in figuring out clusters [8] . When making these maps, it is important to pick colors carefully. The colors need to show the differences between groups or levels of something. And it is good to use colors that people with colorblindness can easily see.

Check our detailed guide on how to create a heatmap here. Also discover our collection of heatmap PowerPoint templates .

Pie charts are circular statistical graphics divided into slices to illustrate numerical proportions. Each slice represents a proportionate part of the whole, making it easy to visualize the contribution of each component to the total.

The size of the pie charts is influenced by the value of data points within each pie. The total of all data points in a pie determines its size. The pie with the highest data points appears as the largest, whereas the others are proportionally smaller. However, you can present all pies of the same size if proportional representation is not required [9] . Sometimes, pie charts are difficult to read, or additional information is required. A variation of this tool can be used instead, known as the donut chart , which has the same structure but a blank center, creating a ring shape. Presenters can add extra information, and the ring shape helps to declutter the graph.

Pie charts are used in business to show percentage distribution, compare relative sizes of categories, or present straightforward data sets where visualizing ratios is essential.

Real-Life Application of Pie Charts

Consider a scenario where you want to represent the distribution of the data. Each slice of the pie chart would represent a different category, and the size of each slice would indicate the percentage of the total portion allocated to that category.

Step 1: Define Your Data Structure

Imagine you are presenting the distribution of a project budget among different expense categories.

• Column A: Expense Categories (Personnel, Equipment, Marketing, Miscellaneous)
• Column B: Budget Amounts ($40,000, $30,000, $20,000, $10,000) Column B represents the values of your categories in Column A.

Step 2: Insert a Pie Chart

Using any of the accessible tools, you can create a pie chart. The most convenient tools for forming a pie chart in a presentation are presentation tools such as PowerPoint or Google Slides.  You will notice that the pie chart assigns each expense category a percentage of the total budget by dividing it by the total budget.

For instance:

• Personnel: $40,000 / ($40,000 + $30,000 + $20,000 + $10,000) = 40%
• Equipment: $30,000 / ($40,000 + $30,000 + $20,000 + $10,000) = 30%
• Marketing: $20,000 / ($40,000 + $30,000 + $20,000 + $10,000) = 20%
• Miscellaneous: $10,000 / ($40,000 + $30,000 + $20,000 + $10,000) = 10%

You can make a chart out of this or just pull out the pie chart from the data.

3D pie charts and 3D donut charts are quite popular among the audience. They stand out as visual elements in any presentation slide, so let’s take a look at how our pie chart example would look in 3D pie chart format.

Step 03: Results Interpretation

The pie chart visually illustrates the distribution of the project budget among different expense categories. Personnel constitutes the largest portion at 40%, followed by equipment at 30%, marketing at 20%, and miscellaneous at 10%. This breakdown provides a clear overview of where the project funds are allocated, which helps in informed decision-making and resource management. It is evident that personnel are a significant investment, emphasizing their importance in the overall project budget.

Pie charts provide a straightforward way to represent proportions and percentages. They are easy to understand, even for individuals with limited data analysis experience. These charts work well for small datasets with a limited number of categories.

However, a pie chart can become cluttered and less effective in situations with many categories. Accurate interpretation may be challenging, especially when dealing with slight differences in slice sizes. In addition, these charts are static and do not effectively convey trends over time.

For more information, check our collection of pie chart templates for PowerPoint .

Histograms present the distribution of numerical variables. Unlike a bar chart that records each unique response separately, histograms organize numeric responses into bins and show the frequency of reactions within each bin [10] . The x-axis of a histogram shows the range of values for a numeric variable. At the same time, the y-axis indicates the relative frequencies (percentage of the total counts) for that range of values.

Whenever you want to understand the distribution of your data, check which values are more common, or identify outliers, histograms are your go-to. Think of them as a spotlight on the story your data is telling. A histogram can provide a quick and insightful overview if you’re curious about exam scores, sales figures, or any numerical data distribution.

Real-Life Application of a Histogram

In the histogram data analysis presentation example, imagine an instructor analyzing a class’s grades to identify the most common score range. A histogram could effectively display the distribution. It will show whether most students scored in the average range or if there are significant outliers.

Step 1: Gather Data

He begins by gathering the data. The scores of each student in class are gathered to analyze exam scores.

After arranging the scores in ascending order, bin ranges are set.

Step 2: Define Bins

Bins are like categories that group similar values. Think of them as buckets that organize your data. The presenter decides how wide each bin should be based on the range of the values. For instance, the instructor sets the bin ranges based on score intervals: 60-69, 70-79, 80-89, and 90-100.

Step 3: Count Frequency

Now, he counts how many data points fall into each bin. This step is crucial because it tells you how often specific ranges of values occur. The result is the frequency distribution, showing the occurrences of each group.

Here, the instructor counts the number of students in each category.

• 60-69: 1 student (Kate)
• 70-79: 4 students (David, Emma, Grace, Jack)
• 80-89: 7 students (Alice, Bob, Frank, Isabel, Liam, Mia, Noah)
• 90-100: 3 students (Clara, Henry, Olivia)

Step 4: Create the Histogram

It’s time to turn the data into a visual representation. Draw a bar for each bin on a graph. The width of the bar should correspond to the range of the bin, and the height should correspond to the frequency.  To make your histogram understandable, label the X and Y axes.

In this case, the X-axis should represent the bins (e.g., test score ranges), and the Y-axis represents the frequency.

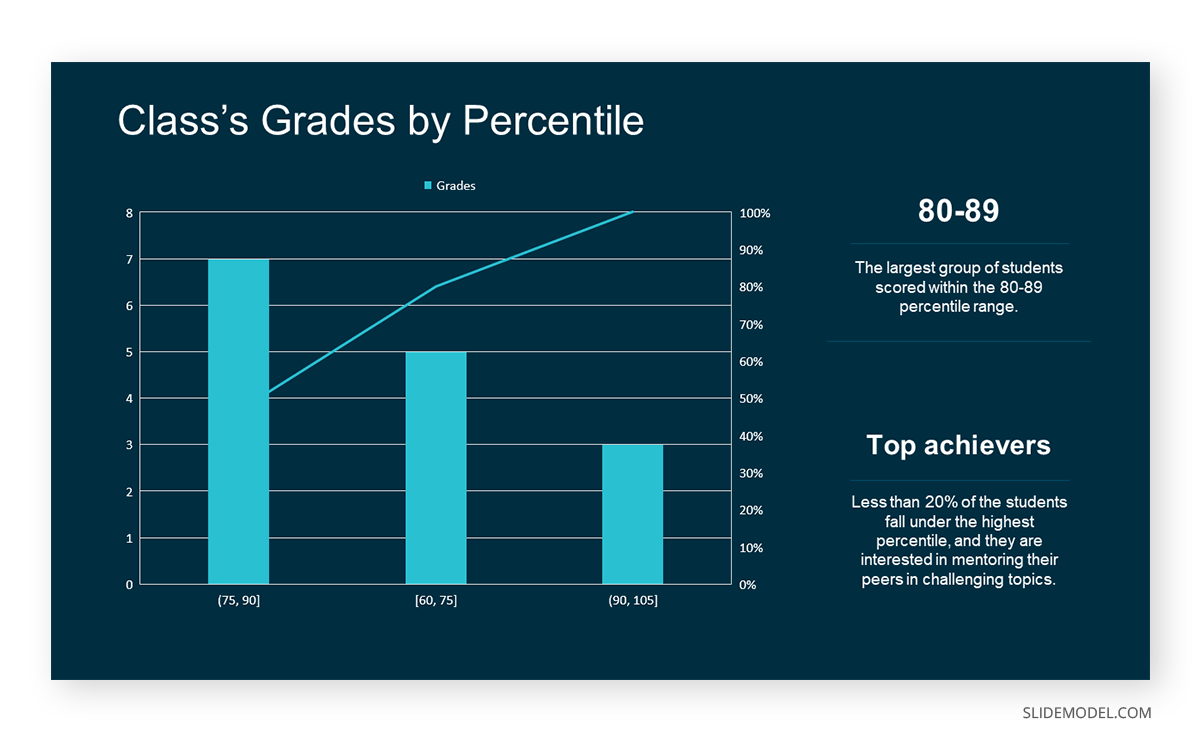
The histogram of the class grades reveals insightful patterns in the distribution. Most students, with seven students, fall within the 80-89 score range. The histogram provides a clear visualization of the class’s performance. It showcases a concentration of grades in the upper-middle range with few outliers at both ends. This analysis helps in understanding the overall academic standing of the class. It also identifies the areas for potential improvement or recognition.

Thus, histograms provide a clear visual representation of data distribution. They are easy to interpret, even for those without a statistical background. They apply to various types of data, including continuous and discrete variables. One weak point is that histograms do not capture detailed patterns in students’ data, with seven compared to other visualization methods.

A scatter plot is a graphical representation of the relationship between two variables. It consists of individual data points on a two-dimensional plane. This plane plots one variable on the x-axis and the other on the y-axis. Each point represents a unique observation. It visualizes patterns, trends, or correlations between the two variables.

Scatter plots are also effective in revealing the strength and direction of relationships. They identify outliers and assess the overall distribution of data points. The points’ dispersion and clustering reflect the relationship’s nature, whether it is positive, negative, or lacks a discernible pattern. In business, scatter plots assess relationships between variables such as marketing cost and sales revenue. They help present data correlations and decision-making.

Real-Life Application of Scatter Plot

A group of scientists is conducting a study on the relationship between daily hours of screen time and sleep quality. After reviewing the data, they managed to create this table to help them build a scatter plot graph:

In the provided example, the x-axis represents Daily Hours of Screen Time, and the y-axis represents the Sleep Quality Rating.

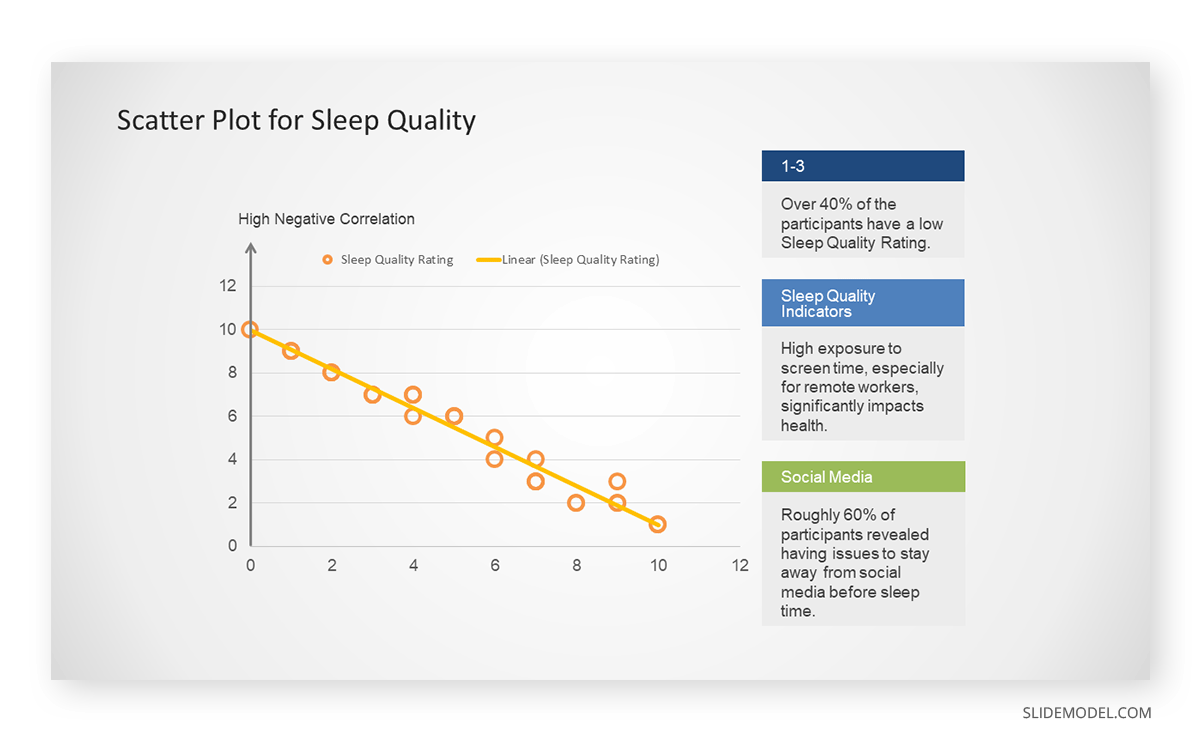
The scientists observe a negative correlation between the amount of screen time and the quality of sleep. This is consistent with their hypothesis that blue light, especially before bedtime, has a significant impact on sleep quality and metabolic processes.

There are a few things to remember when using a scatter plot. Even when a scatter diagram indicates a relationship, it doesn’t mean one variable affects the other. A third factor can influence both variables. The more the plot resembles a straight line, the stronger the relationship is perceived [11] . If it suggests no ties, the observed pattern might be due to random fluctuations in data. When the scatter diagram depicts no correlation, whether the data might be stratified is worth considering.

Choosing the appropriate data presentation type is crucial when making a presentation . Understanding the nature of your data and the message you intend to convey will guide this selection process. For instance, when showcasing quantitative relationships, scatter plots become instrumental in revealing correlations between variables. If the focus is on emphasizing parts of a whole, pie charts offer a concise display of proportions. Histograms, on the other hand, prove valuable for illustrating distributions and frequency patterns. 

Bar charts provide a clear visual comparison of different categories. Likewise, line charts excel in showcasing trends over time, while tables are ideal for detailed data examination. Starting a presentation on data presentation types involves evaluating the specific information you want to communicate and selecting the format that aligns with your message. This ensures clarity and resonance with your audience from the beginning of your presentation.

1. Fact Sheet Dashboard for Data Presentation

Convey all the data you need to present in this one-pager format, an ideal solution tailored for users looking for presentation aids. Global maps, donut chats, column graphs, and text neatly arranged in a clean layout presented in light and dark themes.

Use This Template

2. 3D Column Chart Infographic PPT Template

Represent column charts in a highly visual 3D format with this PPT template. A creative way to present data, this template is entirely editable, and we can craft either a one-page infographic or a series of slides explaining what we intend to disclose point by point.

3. Data Circles Infographic PowerPoint Template

An alternative to the pie chart and donut chart diagrams, this template features a series of curved shapes with bubble callouts as ways of presenting data. Expand the information for each arch in the text placeholder areas.

4. Colorful Metrics Dashboard for Data Presentation

This versatile dashboard template helps us in the presentation of the data by offering several graphs and methods to convert numbers into graphics. Implement it for e-commerce projects, financial projections, project development, and more.

5. Animated Data Presentation Tools for PowerPoint & Google Slides

A slide deck filled with most of the tools mentioned in this article, from bar charts, column charts, treemap graphs, pie charts, histogram, etc. Animated effects make each slide look dynamic when sharing data with stakeholders.

6. Statistics Waffle Charts PPT Template for Data Presentations

This PPT template helps us how to present data beyond the typical pie chart representation. It is widely used for demographics, so it’s a great fit for marketing teams, data science professionals, HR personnel, and more.

7. Data Presentation Dashboard Template for Google Slides

A compendium of tools in dashboard format featuring line graphs, bar charts, column charts, and neatly arranged placeholder text areas. 

8. Weather Dashboard for Data Presentation

Share weather data for agricultural presentation topics, environmental studies, or any kind of presentation that requires a highly visual layout for weather forecasting on a single day. Two color themes are available.

9. Social Media Marketing Dashboard Data Presentation Template

Intended for marketing professionals, this dashboard template for data presentation is a tool for presenting data analytics from social media channels. Two slide layouts featuring line graphs and column charts.

10. Project Management Summary Dashboard Template

A tool crafted for project managers to deliver highly visual reports on a project’s completion, the profits it delivered for the company, and expenses/time required to execute it. 4 different color layouts are available.

11. Profit & Loss Dashboard for PowerPoint and Google Slides

A must-have for finance professionals. This typical profit & loss dashboard includes progress bars, donut charts, column charts, line graphs, and everything that’s required to deliver a comprehensive report about a company’s financial situation.

Overwhelming visuals

One of the mistakes related to using data-presenting methods is including too much data or using overly complex visualizations. They can confuse the audience and dilute the key message.

Inappropriate chart types

Choosing the wrong type of chart for the data at hand can lead to misinterpretation. For example, using a pie chart for data that doesn’t represent parts of a whole is not right.

Lack of context

Failing to provide context or sufficient labeling can make it challenging for the audience to understand the significance of the presented data.

Inconsistency in design

Using inconsistent design elements and color schemes across different visualizations can create confusion and visual disarray.

Failure to provide details

Simply presenting raw data without offering clear insights or takeaways can leave the audience without a meaningful conclusion.

Lack of focus

Not having a clear focus on the key message or main takeaway can result in a presentation that lacks a central theme.

Visual accessibility issues

Overlooking the visual accessibility of charts and graphs can exclude certain audience members who may have difficulty interpreting visual information.

In order to avoid these mistakes in data presentation, presenters can benefit from using presentation templates . These templates provide a structured framework. They ensure consistency, clarity, and an aesthetically pleasing design, enhancing data communication’s overall impact.

Understanding and choosing data presentation types are pivotal in effective communication. Each method serves a unique purpose, so selecting the appropriate one depends on the nature of the data and the message to be conveyed. The diverse array of presentation types offers versatility in visually representing information, from bar charts showing values to pie charts illustrating proportions. 

Using the proper method enhances clarity, engages the audience, and ensures that data sets are not just presented but comprehensively understood. By appreciating the strengths and limitations of different presentation types, communicators can tailor their approach to convey information accurately, developing a deeper connection between data and audience understanding.

If you need a quick method to create a data presentation, check out our  AI presentation maker . A tool in which you add the topic, curate the outline, select a design, and let AI do the work for you.

[1] Government of Canada, S.C. (2021) 5 Data Visualization 5.2 Bar Chart , 5.2 Bar chart .  https://www150.statcan.gc.ca/n1/edu/power-pouvoir/ch9/bargraph-diagrammeabarres/5214818-eng.htm

[2] Kosslyn, S.M., 1989. Understanding charts and graphs. Applied cognitive psychology, 3(3), pp.185-225. https://apps.dtic.mil/sti/pdfs/ADA183409.pdf

[3] Creating a Dashboard . https://it.tufts.edu/book/export/html/1870

[4] https://www.goldenwestcollege.edu/research/data-and-more/data-dashboards/index.html

[5] https://www.mit.edu/course/21/21.guide/grf-line.htm

[6] Jadeja, M. and Shah, K., 2015, January. Tree-Map: A Visualization Tool for Large Data. In GSB@ SIGIR (pp. 9-13). https://ceur-ws.org/Vol-1393/gsb15proceedings.pdf#page=15

[7] Heat Maps and Quilt Plots. https://www.publichealth.columbia.edu/research/population-health-methods/heat-maps-and-quilt-plots

[8] EIU QGIS WORKSHOP. https://www.eiu.edu/qgisworkshop/heatmaps.php

[9] About Pie Charts.  https://www.mit.edu/~mbarker/formula1/f1help/11-ch-c8.htm

[10] Histograms. https://sites.utexas.edu/sos/guided/descriptive/numericaldd/descriptiven2/histogram/ [11] https://asq.org/quality-resources/scatter-diagram

Like this article? Please share

Data Analysis, Data Science, Data Visualization Filed under Design

Related Articles

Filed under Business • October 8th, 2024

Data-Driven Decision Making: Presenting the Process Behind Informed Choices

Discover how to harness data for informed decision-making and create impactful presentations. A detailed guide + templates on DDDM presentation slides.

Filed under Google Slides Tutorials • June 3rd, 2024

How To Make a Graph on Google Slides

Creating quality graphics is an essential aspect of designing data presentations. Learn how to make a graph in Google Slides with this guide.

Filed under Design • March 27th, 2024

How to Make a Presentation Graph

Detailed step-by-step instructions to master the art of how to make a presentation graph in PowerPoint and Google Slides. Check it out!

Leave a Reply

• Translation

Statistics and data presentation: Understanding Variables

By charlesworth author services.

• Charlesworth Author Services
• 21 January, 2021
• Academic Writing Skills

All science is about understanding variability in different characteristics, and most characteristics vary, hence we call the characteristics that we are studying ‘variables. When we work in a quantitative area, we make measurements. The scale of measurement is very important because one criterion for selecting the appropriate statistical technique is the scale of measurement used to measure whatever it is, we are studying.

There are different statistical techniques to use with each kind of measurement.

✓       Nominal Scale is the lowest level of measurement. Sometimes this is referred to as qualitative data – not to be confused with qualitative research. This scale uses numbers to describe names of discrete categories. One determines for each case whether they have or do not have the attribute in question.

✓       Ordinal Scale is used to rank people in order (e.g. least politically active to most politically active). This is the lowest level of quantitative data and involves the process of assignment of numbers to cases in terms of how much of the attribute is possessed by each subject.

✓       Continuous data can assume different values within a range. Interval Scale is where a number assigned is the amount of attribute possessed. Most statistics procedures can be used with interval data. Ratio Scale is considered the highest level of measurement, because all statistics tools can be used on ratio data.

When you read an article, you need to figure out what all the variables are in a study. Then you need to identify three things for each variable one at a time: the scale of measurement; the possible score range; and the meaning of high score and low score. Variables take on different functions in a study. We have to be able to tease these functions out. When you are conducting research, you have to recognize the different variables that are at play in your study so you can account for them during your analyses. Variables can take on different functions within the same study, so don’t classify them at the start. Researchers decide on a classification of variables in each analysis. Let’s take a look at the different classifications of variables.

Classification of variables

•          Dependent Variable : The outcome variable of interest is observed to see whether it is influenced by a manipulated variable. This is called a dependent variable. In other words, a characteristic that is dependent on, or thought to be influenced by, an independent variable. This is sometimes called outcome or response variable.

•         Independent Variable :  In experimental research, the researcher can manipulate one variable and measure the effect of that manipulation on another variable. The variable that is manipulated is called an independent variable. In other words, a characteristic that affects, or is thought to influence an outcome or dependent variable, or an antecedent condition. Independent variables are sometimes called factors, treatments, predictors, or manipulated variables.

In a better scenario, the only consistent feature that varies between an intervention and control group would be the outcome variable of interest. However, this is not generally the case, and we often have confounding or extraneous variables that play a part. When we design our research studies, we need to pay attention to and account for these variables also.

•       Control Variable : any variable that is held constant in a research study by observing only one of the instances or levels. Control variables are not necessarily of central interest, but things that a researcher cannot change or remove from participants. They might be known to exert some influence on the dependent variable. We can ’ t study everything, so a researcher may be interested, for example, in how parental education (and some other variable) is related to reading ability in younger children. He/she happens to know through previous research that gender is related to reading. So, for the purposes of the study, they chose to study only girls. Thus, gender is the control variable and is “ held constant ”.

•         Mediator (Intervening) Variable : a hypothetical variable that explains the relationship but is not observed directly in the research study. Rather, it is inferred from the relationship between the independent and dependent variable. This is an important concept to understand because most theory is based on notions of intervening variables and understanding how or why such effects occur. These variables might be clearly identified before doing a study, i.e. measured and analyzed within a study. Often, mediating variables surface as researchers interpret findings and emerge as suggestions for future research.

•         Moderator Variable : a variable/characteristic that moderates or changes the direction and/or strength of the relationship between two other variables. When, under what conditions, a relationship holds; influences on the strength of the relationship. For example, if a researcher were looking at the relationship between Socio economic status and AIDs prevention, age might be a moderator variable such that the relationship is stronger for older kids than younger kids.

Understanding the distinction between mediators and moderators is not always easy. Basically, in a mediation model the independent variable cannot influence the dependent variable directly and does so by means of another variable – the mediator. As a simple example, older people tend to be better drivers than young people. So, age is a predictor of good driving. However, when we think about why this is the case, we see that older people typically make wiser decisions and so wisdom could be seen as the mediating variable.

There are a number of tests that can be used within your statistical software program to test for mediating and moderating effects. Moderated regression is an example. A moderator analysis is used to determine whether the relationship between two variables depends on (is moderated by) the value of a third variable. You can find online tutorials to explore how this is conducted for the statistical package you are using. Regression can also be used to test for a mediating effect.

Maximise your publication success with Charlesworth Author Services.

Charlesworth Author Services offers statistical analysis for researchers in the field of medical and life sciences articles. This service will help the researcher improve the accuracy and reporting of their data prior to submitting their article to a publisher

To find out more about this service please visit:  How does the Statistical Review Service Work?

Join us on our FREE series of webinars designed to help you understand statistics and data presentation for publication.  

Share with your colleagues

Scientific Editing Services

Sign up – stay updated.

We use cookies to offer you a personalized experience. By continuing to use this website, you consent to the use of cookies in accordance with our Cookie Policy.

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Types of variables and commonly used statistical designs.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 6, 2023 .

• Definition/Introduction

Suitable statistical design represents a critical factor in permitting inferences from any research or scientific study. [1]  Numerous statistical designs are implementable due to the advancement of software available for extensive data analysis. [1]  Healthcare providers must possess some statistical knowledge to interpret new studies and provide up-to-date patient care. We present an overview of the types of variables and commonly used designs to facilitate this understanding. [2]

• Issues of Concern

Individuals who attempt to conduct research and choose an inappropriate design could select a faulty test and make flawed conclusions. This decision could lead to work being rejected for publication or (worse) lead to erroneous clinical decision-making, resulting in unsafe practice. [1]  By understanding the types of variables and choosing tests that are appropriate to the data, individuals can draw appropriate conclusions and promote their work for an application. [3]

To determine which statistical design is appropriate for the data and research plan, one must first examine the scales of each measurement. [4]  Multiple types of variables determine the appropriate design.

Ordinal data (also sometimes referred to as discrete) provide ranks and thus levels of degree between the measurement. [5]  Likert items can serve as ordinal variables, but the Likert scale, the result of adding all the times, can be treated as a continuous variable. [6]  For example, on a 20-item scale with each item ranging from 1 to 5, the item itself can be an ordinal variable, whereas if you add up all items, it could result in a range from 20 to 100. A general guideline for determining if a variable is ordinal vs. continuous: if the variable has more than ten options, it can be treated as a continuous variable. [7]  The following examples are ordinal variables:

• Likert items
• Cancer stages
• Residency Year

Nominal, Categorical, Dichotomous, Binary

Other types of variables have interchangeable terms. Nominal and categorical variables describe samples in groups based on counts that fall within each category, have no quantitative relationships, and cannot be ranked. [8]  Examples of these variables include:

• Service (i.e., emergency, internal medicine, psychiatry, etc.)
• Mode of Arrival (ambulance, helicopter, car)

A dichotomous or a binary variable is in the same family as nominal/categorical, but this type has only two options. Binary logistic regression, which will be discussed below, has two options for the outcome of interest/analysis. Often used as (yes/no), examples of dichotomous or binary variables would be:

• Alive (yes vs. no)
• Insurance (yes vs. no)
• Readmitted (yes vs. no)

With this overview of the types of variables provided, we will present commonly used statistical designs for different scales of measurement. Importantly, before deciding on a statistical test, individuals should perform exploratory data analysis to ensure there are no issues with the data and consider type I, type II errors, and power analysis. Furthermore, investigators should ensure appropriate statistical assumptions. [9] [10]  For example, parametric tests, including some discussed below (t-tests, analysis of variance (ANOVA), correlation, and regression), require the data to have a normal distribution and that the variances within each group are similar. [6] [11]  After eliminating any issues based on exploratory data analysis and reducing the likelihood of committing type I and type II errors, a statistical test can be chosen. Below is a brief introduction to each of the commonly used statistical designs with examples of each type. An example of one research focus, with each type of statistical design discussed, can be found in Table 1 to provide more examples of commonly used statistical designs. 

Commonly Used Statistical Designs

Independent Samples T-test

An independent samples t-test allows a comparison of two groups of subjects on one (continuous) variable. Examples in biomedical research include comparing results of treatment vs. control group and comparing differences based on gender (male vs. female).

Example: Does adherence to the ketogenic diet (yes/no; two groups) have a differential effect on total sleep time (minutes; continuous)?

Paired T-test

A paired t-test analyzes one sample population, measuring the same variable on two different occasions; this is often useful for intervention and educational research.

Example :  Does participating in a research curriculum (one group with intervention) improve resident performance on a test to measure research competence (continuous)?

One-Way Analysis of Variance (ANOVA)

Analysis of variance (ANOVA), as an extension of the t-test, determines differences amongst more than two groups, or independent variables based on a dependent variable. [11]  ANOVA is preferable to conducting multiple t-tests as it reduces the likelihood of committing a type I error.

Example: Are there differences in length of stay in the hospital (continuous) based on the mode of arrival (car, ambulance, helicopter, three groups)?

Repeated Measures ANOVA

Another procedure commonly used if the data for individuals are recurrent (repeatedly measured) is a repeated-measures ANOVA. [1]  In these studies, multiple measurements of the dependent variable are collected from the study participants. [11]  A within-subjects repeated measures ANOVA determines effects based on the treatment variable alone, whereas mixed ANOVAs allow both between-group effects and within-subjects to be considered.

Within-Subjects Example: How does ketamine effect mean arterial pressure (continuous variable) over time (repeated measurement)?

Mixed Example: Does mean arterial pressure (continuous) differ between males and females (two groups; mixed) on ketamine throughout a surgical procedure (over time; repeated measurement)?  

Nonparametric Tests

Nonparametric tests, such as the Mann-Whitney U test (two groups; nonparametric t-test), Kruskal Wallis test (multiple groups; nonparametric ANOVA), Spearman’s rho (nonparametric correlation coefficient) can be used when data are ordinal or lack normality. [3] [5]  Not requiring normality means that these tests allow skewed data to be analyzed; they require the meeting of fewer assumptions. [11]

Example: Is there a relationship between insurance status (two groups) and cancer stage (ordinal)?  

A Chi-square test determines the effect of relationships between categorical variables, which determines frequencies and proportions into which these variables fall. [11]  Similar to other tests discussed, variants and extensions of the chi-square test (e.g., Fisher’s exact test, McNemar’s test) may be suitable depending on the variables. [8]

Example: Is there a relationship between individuals with methamphetamine in their system (yes vs. no; dichotomous) and gender (male or female; dichotomous)?

Correlation

Correlations (used interchangeably with ‘associations’) signal patterns in data between variables. [1]  A positive association occurs if values in one variable increase as values in another also increase. A negative association occurs if variables in one decrease while others increase. A correlation coefficient, expressed as r,  describes the strength of the relationship: a value of 0 means no relationship, and the relationship strengthens as r approaches 1 (positive relationship) or -1 (negative association). [5]

Example: Is there a relationship between age (continuous) and satisfaction with life survey scores (continuous)?

Linear Regression

Regression allows researchers to determine the degrees of relationships between a dependent variable and independent variables and results in an equation for prediction. [11]  A large number of variables are usable in regression methods.

Example: Which admission to the hospital metrics (multiple continuous) best predict the total length of stay (minutes; continuous)?

Binary Logistic Regression

This type of regression, which aims to predict an outcome, is appropriate when the dependent variable or outcome of interest is binary or dichotomous (yes/no; cured/not cured). [12]

Example: Which panel results (multiple of continuous, ordinal, categorical, dichotomous) best predict whether or not an individual will have a positive blood culture (dichotomous/binary)?

The table provides more examples of commonly used statistical designs by providing an example of one research focus and discussing each type of statistical design (see Table. Types of Variables and Statistical Designs).

• Clinical Significance

Though numerous other statistical designs and extensions of methods covered in this article exist, the above information provides a starting point for healthcare providers to become acquainted with variables and commonly used designs. Researchers should study types of variables before determining statistical tests to obtain relevant measures and valid study results. [6]  There is a recommendation to consult a statistician to ensure appropriate usage of the statistical design based on the variables and that the assumptions are upheld. [1]  With the variety of statistical software available, investigators must a priori understand the type of statistical tests when designing a study. [13]  All providers must interpret and scrutinize journal publications to make evidence-based clinical decisions, and this becomes enhanced by a limited but sound understanding of variables and commonly used study designs. [14]

• Nursing, Allied Health, and Interprofessional Team Interventions

All interprofessional healthcare team members need to be familiar with study design and the variables used in studies to accurately evaluate new data and studies as they are published and apply the latest data to patient care and drive optimal outcomes.

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Types of Variables and Statistical Designs.  Contributed by M Huecker, MD, and J Shreffler, PhD

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Types of Variables and Commonly Used Statistical Designs. [Updated 2023 Mar 6]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The future of Cochrane Neonatal. [Early Hum Dev. 2020] The future of Cochrane Neonatal. Soll RF, Ovelman C, McGuire W. Early Hum Dev. 2020 Nov; 150:105191. Epub 2020 Sep 12.
• Review How to study improvement interventions: a brief overview of possible study types. [BMJ Qual Saf. 2015] Review How to study improvement interventions: a brief overview of possible study types. Portela MC, Pronovost PJ, Woodcock T, Carter P, Dixon-Woods M. BMJ Qual Saf. 2015 May; 24(5):325-36. Epub 2015 Mar 25.
• Review How to study improvement interventions: a brief overview of possible study types. [Postgrad Med J. 2015] Review How to study improvement interventions: a brief overview of possible study types. Portela MC, Pronovost PJ, Woodcock T, Carter P, Dixon-Woods M. Postgrad Med J. 2015 Jun; 91(1076):343-54.
• Trends in the Usage of Statistical Software and Their Associated Study Designs in Health Sciences Research: A Bibliometric Analysis. [Cureus. 2021] Trends in the Usage of Statistical Software and Their Associated Study Designs in Health Sciences Research: A Bibliometric Analysis. Masuadi E, Mohamud M, Almutairi M, Alsunaidi A, Alswayed AK, Aldhafeeri OF. Cureus. 2021 Jan 11; 13(1):e12639. Epub 2021 Jan 11.
• Healthcare outcomes assessed with observational study designs compared with those assessed in randomized trials: a meta-epidemiological study. [Cochrane Database Syst Rev. 2024] Healthcare outcomes assessed with observational study designs compared with those assessed in randomized trials: a meta-epidemiological study. Toews I, Anglemyer A, Nyirenda JL, Alsaid D, Balduzzi S, Grummich K, Schwingshackl L, Bero L. Cochrane Database Syst Rev. 2024 Jan 4; 1(1):MR000034. Epub 2024 Jan 4.

Recent Activity

• Types of Variables and Commonly Used Statistical Designs - StatPearls Types of Variables and Commonly Used Statistical Designs - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Types of Variables, Descriptive Statistics, and Sample Size

Feroze kaliyadan, vinay kulkarni.

• Author information
• Article notes
• Copyright and License information

Address for correspondence: Dr. Feroze Kaliyadan, Department of Dermatology, King Faisal University, Saudi Arabia. E-mail: [email protected]

Received 2018 Dec; Accepted 2018 Dec.

This is an open access journal, and articles are distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as appropriate credit is given and the new creations are licensed under the identical terms.

This short “snippet” covers three important aspects related to statistics – the concept of variables , the importance, and practical aspects related to descriptive statistics and issues related to sampling – types of sampling and sample size estimation.

Keywords: Biostatistics , descriptive statistics , sample size , variables

What is a variable?[ 1 , 2 ] To put it in very simple terms, a variable is an entity whose value varies. A variable is an essential component of any statistical data. It is a feature of a member of a given sample or population, which is unique, and can differ in quantity or quantity from another member of the same sample or population. Variables either are the primary quantities of interest or act as practical substitutes for the same. The importance of variables is that they help in operationalization of concepts for data collection. For example, if you want to do an experiment based on the severity of urticaria, one option would be to measure the severity using a scale to grade severity of itching. This becomes an operational variable. For a variable to be “good,” it needs to have some properties such as good reliability and validity, low bias, feasibility/practicality, low cost, objectivity, clarity, and acceptance. Variables can be classified into various ways as discussed below.

Quantitative vs qualitative

A variable can collect either qualitative or quantitative data. A variable differing in quantity is called a quantitative variable (e.g., weight of a group of patients), whereas a variable differing in quality is called a qualitative variable (e.g., the Fitzpatrick skin type)

A simple test which can be used to differentiate between qualitative and quantitative variables is the subtraction test. If you can subtract the value of one variable from the other to get a meaningful result, then you are dealing with a quantitative variable (this of course will not apply to rating scales/ranks).

Quantitative variables can be either discrete or continuous

Discrete variables are variables in which no values may be assumed between the two given values (e.g., number of lesions in each patient in a sample of patients with urticaria).

Continuous variables, on the other hand, can take any value in between the two given values (e.g., duration for which the weals last in the same sample of patients with urticaria). One way of differentiating between continuous and discrete variables is to use the “mid-way” test. If, for every pair of values of a variable, a value exactly mid-way between them is meaningful, the variable is continuous. For example, two values for the time taken for a weal to subside can be 10 and 13 min. The mid-way value would be 11.5 min which makes sense. However, for a number of weals, suppose you have a pair of values – 5 and 8 – the midway value would be 6.5 weals, which does not make sense.

Under the umbrella of qualitative variables, you can have nominal/categorical variables and ordinal variables

Nominal/categorical variables are, as the name suggests, variables which can be slotted into different categories (e.g., gender or type of psoriasis).

Ordinal variables or ranked variables are similar to categorical, but can be put into an order (e.g., a scale for severity of itching).

Dependent and independent variables

In the context of an experimental study, the dependent variable (also called outcome variable) is directly linked to the primary outcome of the study. For example, in a clinical trial on psoriasis, the PASI (psoriasis area severity index) would possibly be one dependent variable. The independent variable (sometime also called explanatory variable) is something which is not affected by the experiment itself but which can be manipulated to affect the dependent variable. Other terms sometimes used synonymously include blocking variable, covariate, or predictor variable. Confounding variables are extra variables, which can have an effect on the experiment. They are linked with dependent and independent variables and can cause spurious association. For example, in a clinical trial for a topical treatment in psoriasis, the concomitant use of moisturizers might be a confounding variable. A control variable is a variable that must be kept constant during the course of an experiment.

Descriptive Statistics

Statistics can be broadly divided into descriptive statistics and inferential statistics.[ 3 , 4 ] Descriptive statistics give a summary about the sample being studied without drawing any inferences based on probability theory. Even if the primary aim of a study involves inferential statistics, descriptive statistics are still used to give a general summary. When we describe the population using tools such as frequency distribution tables, percentages, and other measures of central tendency like the mean, for example, we are talking about descriptive statistics. When we use a specific statistical test (e.g., Mann–Whitney U-test) to compare the mean scores and express it in terms of statistical significance, we are talking about inferential statistics. Descriptive statistics can help in summarizing data in the form of simple quantitative measures such as percentages or means or in the form of visual summaries such as histograms and box plots.

Descriptive statistics can be used to describe a single variable (univariate analysis) or more than one variable (bivariate/multivariate analysis). In the case of more than one variable, descriptive statistics can help summarize relationships between variables using tools such as scatter plots.

Descriptive statistics can be broadly put under two categories:

Sorting/grouping and illustration/visual displays

Summary statistics.

Sorting and grouping

Sorting and grouping is most commonly done using frequency distribution tables. For continuous variables, it is generally better to use groups in the frequency table. Ideally, group sizes should be equal (except in extreme ends where open groups are used; e.g., age “greater than” or “less than”).

Another form of presenting frequency distributions is the “stem and leaf” diagram, which is considered to be a more accurate form of description.

Suppose the weight in kilograms of a group of 10 patients is as follows:

56, 34, 48, 43, 87, 78, 54, 62, 61, 59

The “stem” records the value of the “ten's” place (or higher) and the “leaf” records the value in the “one's” place [ Table 1 ].

Stem and leaf plot

Illustration/visual display of data

The most common tools used for visual display include frequency diagrams, bar charts (for noncontinuous variables) and histograms (for continuous variables). Composite bar charts can be used to compare variables. For example, the frequency distribution in a sample population of males and females can be illustrated as given in Figure 1 .

Composite bar chart

A pie chart helps show how a total quantity is divided among its constituent variables. Scatter diagrams can be used to illustrate the relationship between two variables. For example, global scores given for improvement in a condition like acne by the patient and the doctor [ Figure 2 ].

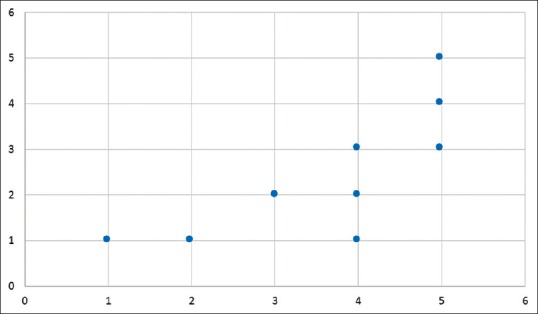
Scatter diagram

Summary statistics

The main tools used for summary statistics are broadly grouped into measures of central tendency (such as mean, median, and mode) and measures of dispersion or variation (such as range, standard deviation, and variance).

Imagine that the data below represent the weights of a sample of 15 pediatric patients arranged in ascending order:

30, 35, 37, 38, 38, 38, 42, 42, 44, 46, 47, 48, 51, 53, 86

Just having the raw data does not mean much to us, so we try to express it in terms of some values, which give a summary of the data.

The mean is basically the sum of all the values divided by the total number. In this case, we get a value of 45.

The problem is that some extreme values (outliers), like “'86,” in this case can skew the value of the mean. In this case, we consider other values like the median, which is the point that divides the distribution into two equal halves. It is also referred to as the 50 th percentile (50% of the values are above it and 50% are below it). In our previous example, since we have already arranged the values in ascending order we find that the point which divides it into two equal halves is the 8 th value – 42. In case of a total number of values being even, we choose the two middle points and take an average to reach the median.

The mode is the most common data point. In our example, this would be 38. The mode as in our case may not necessarily be in the center of the distribution.

The median is the best measure of central tendency from among the mean, median, and mode. In a “symmetric” distribution, all three are the same, whereas in skewed data the median and mean are not the same; lie more toward the skew, with the mean lying further to the skew compared with the median. For example, in Figure 3 , a right skewed distribution is seen (direction of skew is based on the tail); data values' distribution is longer on the right-hand (positive) side than on the left-hand side. The mean is typically greater than the median in such cases.

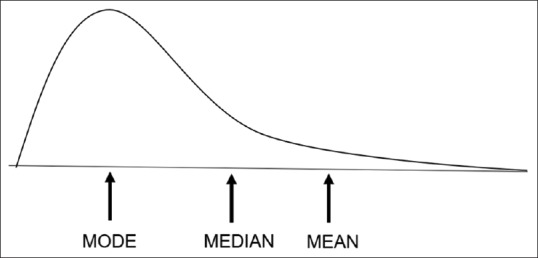
Location of mode, median, and mean

Measures of dispersion

The range gives the spread between the lowest and highest values. In our previous example, this will be 86-30 = 56.

A more valuable measure is the interquartile range. A quartile is one of the values which break the distribution into four equal parts. The 25 th percentile is the data point which divides the group between the first one-fourth and the last three-fourth of the data. The first one-fourth will form the first quartile. The 75 th percentile is the data point which divides the distribution into a first three-fourth and last one-fourth (the last one-fourth being the fourth quartile). The range between the 25 th percentile and 75 th percentile is called the interquartile range.

Variance is also a measure of dispersion. The larger the variance, the further the individual units are from the mean. Let us consider the same example we used for calculating the mean. The mean was 45.

For the first value (30), the deviation from the mean will be 15; for the last value (86), the deviation will be 41. Similarly we can calculate the deviations for all values in a sample. Adding these deviations and averaging will give a clue to the total dispersion, but the problem is that since the deviations are a mix of negative and positive values, the final total becomes zero. To calculate the variance, this problem is overcome by adding squares of the deviations. So variance would be the sum of squares of the variation divided by the total number in the population (for a sample we use “n − 1”). To get a more realistic value of the average dispersion, we take the square root of the variance, which is called the “standard deviation.”

The box plot

The box plot is a composite representation that portrays the mean, median, range, and the outliers [ Figure 4 ].

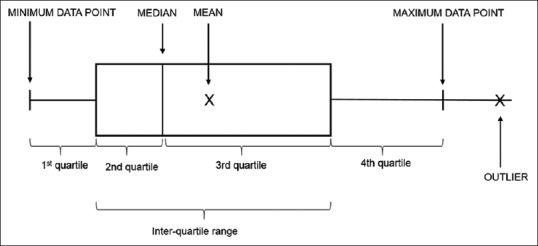
The concept of skewness and kurtosis

Skewness is a measure of the symmetry of distribution. Basically if the distribution curve is symmetric, it looks the same on either side of the central point. When this is not the case, it is said to be skewed. Kurtosis is a representation of outliers. Distributions with high kurtosis tend to have “heavy tails” indicating a larger number of outliers, whereas distributions with low kurtosis have light tails, indicating lesser outliers. There are formulas to calculate both skewness and kurtosis [Figures 5 – 8 ].

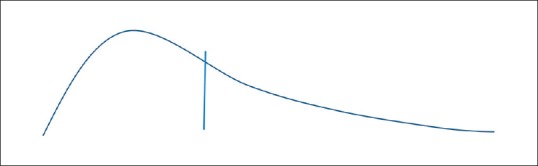
Positive skew

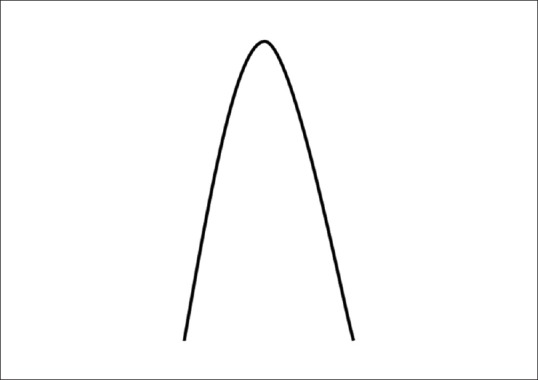
High kurtosis (positive kurtosis – also called leptokurtic)

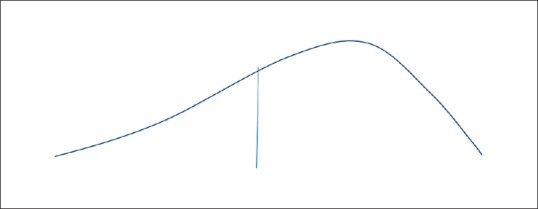
Negative skew

Low kurtosis (negative kurtosis – also called “Platykurtic”)

Sample Size

In an ideal study, we should be able to include all units of a particular population under study, something that is referred to as a census.[ 5 , 6 ] This would remove the chances of sampling error (difference between the outcome characteristics in a random sample when compared with the true population values – something that is virtually unavoidable when you take a random sample). However, it is obvious that this would not be feasible in most situations. Hence, we have to study a subset of the population to reach to our conclusions. This representative subset is a sample and we need to have sufficient numbers in this sample to make meaningful and accurate conclusions and reduce the effect of sampling error.

We also need to know that broadly sampling can be divided into two types – probability sampling and nonprobability sampling. Examples of probability sampling include methods such as simple random sampling (each member in a population has an equal chance of being selected), stratified random sampling (in nonhomogeneous populations, the population is divided into subgroups – followed be random sampling in each subgroup), systematic (sampling is based on a systematic technique – e.g., every third person is selected for a survey), and cluster sampling (similar to stratified sampling except that the clusters here are preexisting clusters unlike stratified sampling where the researcher decides on the stratification criteria), whereas nonprobability sampling, where every unit in the population does not have an equal chance of inclusion into the sample, includes methods such as convenience sampling (e.g., sample selected based on ease of access) and purposive sampling (where only people who meet specific criteria are included in the sample).

An accurate calculation of sample size is an essential aspect of good study design. It is important to calculate the sample size much in advance, rather than have to go for post hoc analysis. A sample size that is too less may make the study underpowered, whereas a sample size which is more than necessary might lead to a wastage of resources.

We will first go through the sample size calculation for a hypothesis-based design (like a randomized control trial).

The important factors to consider for sample size calculation include study design, type of statistical test, level of significance, power and effect size, variance (standard deviation for quantitative data), and expected proportions in the case of qualitative data. This is based on previous data, either based on previous studies or based on the clinicians' experience. In case the study is something being conducted for the first time, a pilot study might be conducted which helps generate these data for further studies based on a larger sample size). It is also important to know whether the data follow a normal distribution or not.

Two essential aspects we must understand are the concept of Type I and Type II errors. In a study that compares two groups, a null hypothesis assumes that there is no significant difference between the two groups, and any observed difference being due to sampling or experimental error. When we reject a null hypothesis, when it is true, we label it as a Type I error (also denoted as “alpha,” correlating with significance levels). In a Type II error (also denoted as “beta”), we fail to reject a null hypothesis, when the alternate hypothesis is actually true. Type II errors are usually expressed as “1- β,” correlating with the power of the test. While there are no absolute rules, the minimal levels accepted are 0.05 for α (corresponding to a significance level of 5%) and 0.20 for β (corresponding to a minimum recommended power of “1 − 0.20,” or 80%).

Effect size and minimal clinically relevant difference

For a clinical trial, the investigator will have to decide in advance what clinically detectable change is significant (for numerical data, this is could be the anticipated outcome means in the two groups, whereas for categorical data, it could correlate with the proportions of successful outcomes in two groups.). While we will not go into details of the formula for sample size calculation, some important points are as follows:

In the context where effect size is involved, the sample size is inversely proportional to the square of the effect size. What this means in effect is that reducing the effect size will lead to an increase in the required sample size.

Reducing the level of significance (alpha) or increasing power (1-β) will lead to an increase in the calculated sample size.

An increase in variance of the outcome leads to an increase in the calculated sample size.

A note is that for estimation type of studies/surveys, sample size calculation needs to consider some other factors too. This includes an idea about total population size (this generally does not make a major difference when population size is above 20,000, so in situations where population size is not known we can assume a population of 20,000 or more). The other factor is the “margin of error” – the amount of deviation which the investigators find acceptable in terms of percentages. Regarding confidence levels, ideally, a 95% confidence level is the minimum recommended for surveys too. Finally, we need an idea of the expected/crude prevalence – either based on previous studies or based on estimates.

Sample size calculation also needs to add corrections for patient drop-outs/lost-to-follow-up patients and missing records. An important point is that in some studies dealing with rare diseases, it may be difficult to achieve desired sample size. In these cases, the investigators might have to rework outcomes or maybe pool data from multiple centers. Although post hoc power can be analyzed, a better approach suggested is to calculate 95% confidence intervals for the outcome and interpret the study results based on this.

Financial support and sponsorship

Conflicts of interest.

There are no conflicts of interest.

• 1. Seltman HJ, editor. Experimental Design and Analysis. 1st ed. Pittsburgh, PA: Carnegie Mellon University; 2012. Variable classification; pp. 9–18. [ Google Scholar ]
• 2. Hoeks S, Kardys I, Lenzen M, van Domburg R, Boersma E. Tools and techniques – Statistics: Descriptive statistics. EuroIntervention. 2013;9:1001–3. doi: 10.4244/EIJV9I8A167. [ DOI ] [ PubMed ] [ Google Scholar ]
• 3. Seltman HJ, editor. Experimental Design and Analysis. 1st ed. Pittsburgh, PA: Carnegie Mellon University; 2012. Review of probability; pp. 19–60. [ Google Scholar ]
• 4. Nick TG. Descriptive statistics. Methods Mol Biol. 2007;404:33–52. doi: 10.1007/978-1-59745-530-5_3. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Endacott R, Botti M. Clinical research 3: Sample selection. Accid Emerg Nurs. 2007;15:234–8. doi: 10.1016/j.aaen.2006.12.006. [ DOI ] [ PubMed ] [ Google Scholar ]
• 6. Hazra A, Gogtay N. Biostatistics series module 5: Determining sample size. Indian J Dermatol. 2016;61:496–504. doi: 10.4103/0019-5154.173988. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (702.9 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections