newton's apple experiment

• History Classics
• Your Profile
• Find History on Facebook (Opens in a new window)
• Find History on Twitter (Opens in a new window)
• Find History on YouTube (Opens in a new window)
• Find History on Instagram (Opens in a new window)
• Find History on TikTok (Opens in a new window)
• This Day In History
• History Podcasts
• History Vault

Did an apple really fall on Isaac Newton’s head?

By: Elizabeth Nix

Updated: September 1, 2018 | Original: November 13, 2015

Legend has it that a young Isaac Newton was sitting under an apple tree when he was bonked on the head by a falling piece of fruit, a 17th-century “aha moment” that prompted him to suddenly come up with his law of gravity. In reality, things didn’t go down quite like that. Newton, the son of a farmer, was born in 1642 near Grantham, England, and entered Cambridge University in 1661. Four years later, following an outbreak of the bubonic plague, the school temporarily closed, forcing Newton to move back to his childhood home, Woolsthorpe Manor. It was during this period at Woolsthorpe (Newton returned to Cambridge in 1667) that he was in the orchard there and witnessed an apple drop from a tree. There’s no evidence to suggest the fruit actually landed on his head, but Newton’s observation caused him to ponder why apples always fall straight to the ground (rather than sideways or upward) and helped inspired him to eventually develop his law of universal gravitation. In 1687, Newton first published this principle, which states that every body in the universe is attracted to every other body with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them, in his landmark work the “Principia,” which also features his three laws of motion.

In 1726, Newton shared the apple anecdote with William Stukeley, who included it in a biography, “Memoirs of Sir Isaac Newton’s Life,” published in 1752. According to Stukeley, “After dinner, the weather being warm, we went into the garden, & drank thea under the shade of some apple trees… he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind…. occasion’d by the fall of an apple, as he sat in a contemplative mood.”

The esteemed mathematician and physicist died in 1727 and was buried at Westminster Abbey. His famous apple tree continues to grow at Woolsthorpe Manor.

Sign up for Inside History

Get HISTORY’s most fascinating stories delivered to your inbox three times a week.

By submitting your information, you agree to receive emails from HISTORY and A+E Networks. You can opt out at any time. You must be 16 years or older and a resident of the United States.

More details : Privacy Notice | Terms of Use | Contact Us

Advertisement

Newton's apple: The real story

By Amanda Gefter

18 January 2010

We’ve all heard the story. A young Isaac Newton is sitting beneath an apple tree contemplating the mysterious universe. Suddenly –  boink!  -an apple hits him on the head. “Aha!” he shouts, or perhaps, “Eureka!” In a flash he understands that the very same force that brought the apple crashing toward the ground also keeps the moon falling toward the Earth and the Earth falling toward the sun: gravity.

Or something like that. The apocryphal story is one of the most famous in the history of science and now you can see for yourself what Newton actually said. Squirreled away in the archives of London’s  Royal Society  was a manuscript containing the truth about the apple.

It is the manuscript for what would become a biography of Newton entitled  Memoirs of Sir Isaac Newton’s Life written by William Stukeley, an archaeologist and one of Newton’s first biographers, and published in 1752. Newton told the apple story to Stukeley, who relayed it as such:

“After dinner, the weather being warm, we went into the garden and drank thea, under the shade of some apple trees…he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. It was occasion’d by the fall of an apple, as he sat in contemplative mood. Why should that apple always descend perpendicularly to the ground, thought he to himself…”

The Royal Society has made the manuscript available today for the first time in a fully interactive digital form on their website at royalsociety.org/turning-the-pages . The digital release is occurring on the same day as the publication of  Seeing Further  (HarperPress, £25), an illustrated history of the Royal Society edited by  Bill Bryson , which marks the Royal Society’s 350th anniversary this year.

So it turns out the apple story is true – for the most part. The apple may not have hit Newton in the head, but I’ll still picture it that way. Meanwhile, three and a half centuries and an Albert Einstein later, physicists still don’t  really  understand gravity. We’re gonna need a bigger apple.

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

More from New Scientist

Explore the latest news, articles and features

Einstein’s theories tested on the largest scale ever – he was right

A unique pair of galactic lenses may help solve a cosmological riddle

Subscriber-only

Solving Stephen Hawking’s black hole paradox has raised new mysteries

This test could reveal whether gravity is subject to quantum weirdness

Popular articles.

Trending New Scientist articles

Isaac Newton: Who He Was, Why Apples Are Falling

Sir Isaac Newton was born especially tiny but grew into a massive intellect and still looms large, thanks to his findings on gravity, light, motion, mathematics, and more.

Mathematics, Physics

Isaac Newton Kneller Painting

Far more than just discovering the laws of gravity, Sir Isaac Newton was also responsible for working out many of the principles of visible light and the laws of motion, and contributing to calculus.

Photograph of Sir Godfrey Kneller painting by Science Source

Sir Isaac Newton was a tiny man in real life. But he was a giant in the world of science. Newton created the theory of gravity around 1665 or 1666. He came up with the idea that every physical object, whether it's a person, an apple or a planet, exerts a force on other physical objects. A force is a push or pull in a certain direction. The bigger the body, the stronger the force . There are different types of forces , but this one is called gravitational. Some say that Newton came up with his ideas about gravity after watching an apple fall. He wondered why the apple fell straight down. Why didn't it fall sideways, or even up toward the sky? Gravity does not just make apples fall from trees. It also holds us on the ground. Newton showed that gravity even makes the moon circle around Earth, and Earth around the sun, Martin Rees says. He was president of Britain's Royal Society. The Royal Society is the United Kingdom's national academy of science. Newton's Schooling Newton was born on January 4, 1643, in Lincolnshire, England. As a kid, he liked building models. He once built a tiny mill. It could grind real flour. It was even powered by a mouse running in a wheel. In 1661, Newton went to the University of Cambridge. At first, he did not stand out as a student. In 1665, the school closed for a time because of the bubonic plague . This deadly disease killed thousands of people. Newton went home for two years. This is when he got his apple-falling idea. In 1667, he went back to Cambridge and became a math teacher until 1696. Newton Changes Science Forever The theory of gravity was just one of Newton's discoveries. He also loved calculus. This is a mathematical subject that studies rates. A rate is the measurement of how much something changes. Newton's ideas in calculus are still used today. Newton also studied optics, the science of light. He found out that white light is not just white. It is actually a mix of all the colors of the rainbow. Newton used his knowledge of light to make better telescopes. Following his apple idea, Newton wrote three laws of motion. These laws changed all of science, and are still used by scientists today. First Law of Motion: Inertia An object that sits still will remain still unless a force is applied to it. An object that is moving will keep moving along a straight line unless an outside force is applied to it. Second Law of Motion: Acceleration An object will accelerate if force is applied to it. Acceleration is the change of an object's speed. The acceleration will happen in the same direction as the force. This idea can also be written as force equals mass times acceleration, or F = ma. Third Law of Motion: Action and Reaction For every action there is always an equal and opposite reaction. Newton's Published Work Newton published his findings in 1687, in a book called Philosophiae Naturalis Principia Mathematica . Usually people just call it the Principia . When it came out, not many people read or understood the book, mathematician Robert Wilson says. Still, "everyone knew that it was a great work." Perceptions of Isaac Newton Newton made many discoveries, but he wasn't well-liked. As a young man, Newton preferred being alone. When he was older, he was not kind to other scientists. He sometimes tried to ruin their work, Rees says. When he was older, Newton worked in British government. At one point, he led the British Mint, which is the part of government that makes coins for the country. When someone was caught making fake coins, they were sometimes sentenced to death. Newton thought this was a good thing. He had no mercy, Sir David Wallace says. He was the head of the Isaac Newton Institute in Cambridge, England. In 1727, at age 84, Sir Isaac Newton died in his sleep. He was buried in Westminster Abbey in London.

Media Credits

The audio, illustrations, photos, and videos are credited beneath the media asset, except for promotional images, which generally link to another page that contains the media credit. The Rights Holder for media is the person or group credited.

Last Updated

September 27, 2024

User Permissions

For information on user permissions, please read our Terms of Service. If you have questions about how to cite anything on our website in your project or classroom presentation, please contact your teacher. They will best know the preferred format. When you reach out to them, you will need the page title, URL, and the date you accessed the resource.

If a media asset is downloadable, a download button appears in the corner of the media viewer. If no button appears, you cannot download or save the media.

Text on this page is printable and can be used according to our Terms of Service .

Interactives

Any interactives on this page can only be played while you are visiting our website. You cannot download interactives.

Related Resources

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Request a Demo
• Get A Quote
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Lab Equipment
• Lab Procedures
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Chemical Reactions Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Task Tracker Directions
• Conceptual Physics Course
• On-Level Physics Course
• Honors Physics Course
• Chemistry Concept Builders
• All Chemistry Resources
• Users Voice
• Tasks and Classes
• Webinars and Trainings
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• Measurement and Calculations
• Elements, Atoms, and Ions
• Compounds,Names, and Formulas
• The Modern Atomic Model
• Chemical Bonding
• The Mole and its Applications
• Chemical Reactions
• Stoichiometry
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Solution Guide Corrections
• Motion in One Dimension
• Work, Energy and Power
• Chemistry of Matter
• Measurement and the Metric System
• Early Atomic Models
• Names and Formulas
• The Modern Model of the Atom
• Algebra Based On-Level Physics
• Honors Physics
• Conceptual Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• The Apple, the Moon, and the Inverse Square Law
• Gravity is More Than a Name
• Newton's Law of Universal Gravitation
• Cavendish and the Value of G
• The Value of g

• The paths of the planets about the sun are elliptical in shape, with the center of the sun being located at one focus. (The Law of Ellipses)
• An imaginary line drawn from the center of the sun to the center of the planet will sweep out equal areas in equal intervals of time. (The Law of Equal Areas)
• The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of their average distances from the sun. (The Law of Harmonies)

(Further discussion of these three laws is given in Lesson 4 .)

While Kepler's laws provided a suitable framework for describing the motion and paths of planets about the sun, there was no accepted explanation for why such paths existed. The cause for how the planets moved as they did was never stated. Kepler could only suggest that there was some sort of interaction between the sun and the planets that provided the driving force for the planet's motion. To Kepler, the planets were somehow "magnetically" driven by the sun to orbit in their elliptical trajectories. There was however no interaction between the planets themselves.

Newton's Mountain Thought Experiment

A survey of Newton's writings reveals an illustration similar to the one shown at the right. The illustration was accompanied by an extensive discussion of the motion of the moon as a projectile. Newton's reasoning proceeded as follows. Suppose a cannonball is fired horizontally from a very high mountain in a region devoid of air resistance. In the absence of gravity, the cannonball would travel in a straight-line, tangential path. Yet in the presence of gravity, the cannonball would drop below this straight-line path and eventually fall to Earth (as in path A ). Now suppose that the cannonball is fired horizontally again, yet with a greater speed. In this case, the cannonball would still fall below its straight-line tangential path and eventually drop to earth. Only this time, the cannonball would travel further before striking the ground (as in path B ). Now suppose that there is a speed at which the cannonball could be fired such that the trajectory of the falling cannonball matched the curvature of the earth. If such a speed could be obtained, then the cannonball would fall around the earth instead of into it. The cannonball would fall towards the Earth without ever colliding into it and subsequently become a satellite orbiting in circular motion (as in path C ). And then at even greater launch speeds, a cannonball would once more orbit the earth, but in an elliptical path (as in path D ). The motion of the cannonball orbiting to the earth under the influence of gravity is analogous to the motion of the moon orbiting the Earth. And if the orbiting moon can be compared to the falling cannonball, it can even be compared to a falling apple. The same force that causes objects on Earth to fall to the earth also causes objects in the heavens to move along their circular and elliptical paths. Quite amazingly, the laws of mechanics that govern the motions of objects on Earth also govern the movement of objects in the heavens.

Newton's Argument for Gravity Being Universal

Of course, Newton's dilemma was to provide reasonable evidence for the extension of the force of gravity from earth to the heavens. The key to this extension demanded that he be able to show how the affect of gravity is diluted with distance. It was known at the time, that the force of gravity causes earthbound objects (such as falling apples) to accelerate towards the earth at a rate of 9.8 m/s 2 . And it was also known that the moon accelerated towards the earth at a rate of 0.00272 m/s 2 . If the same force that causes the acceleration of the apple to the earth also causes the acceleration of the moon towards the earth, then there must be a plausible explanation for why the acceleration of the moon is so much smaller than the acceleration of the apple. What is it about the force of gravity that causes the more distant moon to accelerate at a rate of acceleration that is approximately 1/3600-th the acceleration of the apple?

Newton knew that the force of gravity must somehow be "diluted" by distance. But how? What mathematical reality is intrinsic to the force of gravity that causes it to be inversely dependent upon the distance between the objects?

The riddle is solved by a comparison of the distance from the apple to the center of the earth with the distance from the moon to the center of the earth. The moon in its orbit about the earth is approximately 60 times further from the earth's center than the apple is. The mathematical relationship becomes clear. The force of gravity between the earth and any object is inversely proportional to the square of the distance that separates that object from the earth's center. The moon, being 60 times further away than the apple, experiences a force of gravity that is 1/(60) 2 times that of the apple. The force of gravity follows an inverse square law .

The relationship between the force of gravity ( F grav ) between the earth and any other object and the distance that separates their centers ( d ) can be expressed by the following relationship

Since the distance d is in the denominator of this relationship, it can be said that the force of gravity is inversely related to the distance. And since the distance is raised to the second power, it can be said that the force of gravity is inversely related to the square of the distance. This mathematical relationship is sometimes referred to as an inverse square law since one quantity depends inversely upon the square of the other quantity. The inverse square relation between the force of gravity and the distance of separation provided sufficient evidence for Newton's explanation of why gravity can be credited as the cause of both the falling apple's acceleration and the orbiting moon's acceleration.

Using Equations as a Guide to Thinking

We would like to suggest ....

freestar.config.enabled_slots.push({ placementName: "physicsclassroom_incontent_3", slotId: "physicsclassroom_incontent_3" });

Check your understanding.

1 . Suppose that two objects attract each other with a gravitational force of 16 units. If the distance between the two objects is doubled, what is the new force of attraction between the two objects?

Answer: F = 4 units

If the distance is increased by a factor of 2, then force will be decreased by a factor of 4 (2 2 ). The new force is then 1/4 of the original 16 units.

F = (16 N) / 4 = 4 units

2. Suppose that two objects attract each other with a gravitational force of 16 units. If the distance between the two objects is tripled, then what is the new force of attraction between the two objects?

Answer: F = 1.78 units

If the distance is increased by a factor of 3, then force will be decreased by a factor of 9 (3 2 ). The new force is then 1/9 of the original 16 units.

F = (16 N) / 9 = 1.78 units

3. Suppose that two objects attract each other with a gravitational force of 16 units. If the distance between the two objects is reduced in half, then what is the new force of attraction between the two objects?

Answer: F = 64 units

If the distance is decreased by a factor of 2, then force will be increased by a factor of 4 (2 2 ). The new force is then 4 times the original 16 units.

F = (16 N) • 4 = 64 units

4. Suppose that two objects attract each other with a gravitational force of 16 units. If the distance between the two objects is reduced by a factor of 5, then what is the new force of attraction between the two objects?  

Answer: F = 400 units

If the distance is decreased by a factor of 5, then force will be increased by a factor of 25 (5 2 ). The new force is then 25 times the original 16 units.

F = (16 N) • 25 = 400 units

5. Having recently completed his first Physics course, Noah Formula has devised a new business plan based on his teacher's Physics for Better Living theme. Noah learned that objects weigh different amounts at different distances from Earth's center. His plan involves buying gold by the weight at one altitude and then selling it at another altitude at the same price per weight. Should Noah buy at a high altitude and sell at a low altitude or vice versa?

To profit, buy at a high altitude and sell at a low one .

Gold will weigh less at a high altitude and so you will get more gold for your money by buying at the high altitude. Then sell at a low altitude where the gold will weigh more than it did where it was purchased. This illustrates the inverse relationship between force of gravity (a.k.a. "weight") and distance from Earth's center.

• Kepler's Three Laws

How a falling apple could have helped Newton discover universal gravity

• Regular Article
• Published: 12 January 2024
• Volume 49 , article number  1 , ( 2024 )

Cite this article

• Gennady Gorelik   ORCID: orcid.org/0009-0007-7867-2893 1  

298 Accesses

Explore all metrics

The article delves into the intriguing disagreement among historians of science regarding the origin of the idea of universal gravity. Prominent researchers of the genesis of Newton's Principia did not believe that he could have come up with this idea in 1666, after observing a falling apple, as he claimed. On the other hand, prominent biographers of Newton did believe. The proposed key to solving this paradox is a thought experiment described in Newton's manuscript, ‘The System of the World,’ which preceded the creation of his ‘Principia.’ According to the proposed ‘subjunctive’ scenario, it was possible to come from the motion of a projectile to the concept of universal gravity, relying only on the knowledge and skills of Galileo in 1611.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Revisiting Einstein’s Happiest Thought. From the Physiology of Perception to Experimental Propositions and Principles in the History of Relativity

Newton’s Apple and Einstein’s Time Warp, New Ideas in Teaching Gravity

How John Wheeler Lost His Faith in the Law

Cohen, I. Bernard. 1971. Introduction to Newton's ‘Principia’ . United Kingdom: Harvard University Press.

Book   Google Scholar  

Cohen, I. Bernard. 1992. The Birth of a New Physics . New York: Penguin.

Google Scholar  

Dyson, Freeman. 1958. Innovation in Physics. Scientific American No. 3: 74-82.

Article   Google Scholar  

Einstein, Albert. 1930. Science and God. A German Dialog, Forum and Century 83:373-379.

Einstein, Albert. 1949. Reply to criticisms. In: Schilpp PA (ed.) Albert Einstein: Philosopher-Scientist. Evanston, Ill.: Library of Living Philosophers.

Einstein, Albert. 1950. Out of My Later Years. New York: Philosophical Library.

Einstein, Albert. 1952. Foreword. In: Galileo Galilei. Dialogue concerning the two chief world systems, Ptolemaic and Copernican . Berkeley and Los Angeles: University of California Press. 1967: vii-xx.

Einstein, Albert. 1960. Ideas and Opinions. New York: Crown Publishers.

Einstein, Albert. 1993. Letters to Solovine . New York: Carol Publishing Group.

Feynman, Richard. 2005. The Pleasure of Finding Things Out. New York: Basic Books.

Galilei, Galileo. 1914. Dialogues concerning two new sciences . Transl. H. Crew and A. De Salvio. New York: Macmillan.

Galilei, Galileo. 1953. Dialogue Concerning the Two Chief World Systems, Ptolemaic and Copernican . Translated by Stillman Drake. Foreword by Albert Einstein. Berkeley: University of California Press.

Gorelik, Gennady. 2017. A Galilean Answer to the Needham Question. Philosophia Scientiæ 21(1): 93–110.

Gorelik, Gennady. 2023. The Concept of Modern Physics and an Extended Needham Question. Epistemology & Philosophy of Science 60(4): 158–172.

Heilbron, John L. 2010. Galileo . Oxford University Press.

Herivel, John. 1965. The background to Newton’s Principia. A Study of Newton’s Dynamical Researches in the Years 1664–84. Oxford: Oxford University Press.

Iliffe, Rob and George E. Smith (eds.). 2016. The Cambridge companion to Newton. 2nd edition. Cambridge University Press.

Kepler, Johannes. 2003. Kepler's Somnium: The Dream, Or Posthumous Work on Lunar Astronomy. United Kingdom: Dover Publications.

Newton, Isaac. 1728. A Treatise of the System of the World . https://books.google.com/books?id=rEYUAAAAQAAJ . https://en.wikisource.org/wiki/The_Mathematical_Principles_of_Natural_Philosophy_(1846)/The_System_of_the_World Accessed 10/3/2023.

Stukeley, William. 1752. Memoirs of Sir Isaac Newton's life (MS). Newton Project. https://www.newtonproject.ox.ac.uk/view/texts/normalized/OTHE00001 Accessed 10/3/2023.

Topper, D. and D. E. Vincent. 1999. An analysis of Newton’s projectile diagram. European Journal of Physics 20: 59-66

Article   ADS   Google Scholar  

van Helden, A. 1985. Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley . University of Chicago Press

Vavilov, Sergey. 1989. Isaak N'yuton [Isaac Newton]. Moscow: Nauka, 1989. (In Russian)

Westfall, Richard. 1971. Force in Newton's physics: the science of dynamics in the 17th century. New York : American Elsevier.

Westfall, Richard. 2010. Never at Rest: A Biography of Isaac Newton . Cambridge: Cambridge University Press.

Whiteside, D. T. 1966. Newton's marvellous year: 1666 and all that. Notes and Records of the Royal Society of London . 21 (1): 32-41.

Article   MathSciNet   Google Scholar  

Whiteside, D. T. 1991. The Prehistory of the Principia from 1664 to 1686. Notes and Records of the Royal Society of London. 45(1):11-61.

Download references

Acknowledgements

I am grateful to Vitaly Matsarsky and Sergey Zelensky for stimulating discussions and to the anonymous reviewers for their stimulating suggestions.

Author information

Authors and affiliations.

Center for Philosophy and History of Science, Boston University, Boston, MA, USA

Gennady Gorelik

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Gennady Gorelik .

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Gorelik, G. How a falling apple could have helped Newton discover universal gravity. EPJ H 49 , 1 (2024). https://doi.org/10.1140/epjh/s13129-023-00065-0

Download citation

Received : 12 October 2023

Accepted : 01 December 2023

Published : 12 January 2024

DOI : https://doi.org/10.1140/epjh/s13129-023-00065-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research

Stay up to date with notifications from The Independent

Notifications can be managed in browser preferences.

• UK Politics
• News Videos
• Paris 2024 Olympics
• Rugby Union
• Sport Videos
• John Rentoul
• Mary Dejevsky
• Andrew Grice
• Sean O’Grady
• Photography
• Theatre & Dance
• Culture Videos
• Fitness & Wellbeing
• Food & Drink
• Health & Families
• Royal Family
• Electric Vehicles
• Car Insurance Deals
• Lifestyle Videos
• Home & Garden
• Broadband deals
• Fashion & Beauty
• Travel & Outdoors
• Sports & Fitness
• Hotel Reviews
• News & Advice
• Simon Calder
• Australia & New Zealand
• South America
• C. America & Caribbean
• Middle East
• Politics Explained
• News Analysis
• Today’s Edition
• Climate 100
• Sustainable Living
• Climate Videos
• Solar Panels
• Behind The Headlines
• On The Ground
• Decomplicated
• You Ask The Questions
• Binge Watch
• Travel Smart
• Watch on your TV
• Crosswords & Puzzles
• Most Commented
• Newsletters
• Ask Me Anything
• Virtual Events
• Wine Offers
• Betting Sites
• Casino Sites

Thank you for registering

Please refresh the page or navigate to another page on the site to be automatically logged in Please refresh your browser to be logged in

The core of truth behind Sir Isaac Newton's apple

The manuscript that gave rise to one of science's best-known anecdotes is now online., independent premium, subscribe to independent premium to bookmark this article.

Want to bookmark your favourite articles and stories to read or reference later? Start your Independent Premium subscription today.

Sign up for our free Health Check email to receive exclusive analysis on the week in health

Get our free health check email.

It is one of the most famous anecdotes in the history of science. The young Isaac Newton is sitting in his garden when an apple falls on his head and, in a stroke of brilliant insight, he suddenly comes up with his theory of gravity. The story is almost certainly embellished, both by Newton and the generations of storytellers who came after him. But from today anyone with access to the internet can see for themselves the first-hand account of how a falling apple inspired the understanding of gravitational force.

The Royal Society in London is making available in digital form the key original manuscript that describes how Newton devised his theory of gravity after witnessing an apple falling from a tree in his mother's garden in Lincolnshire, although there is no evidence to suggest that it hit him on the head.

It was 1666, and the plague had closed many public buildings and meetings. Newton had to abandon Cambridge for Woolsthorpe Manor, near Grantham in Lincolnshire, the modest house where he was born, to contemplate the stellar problems he had been pursuing at the university.

He was particularly obsessed by the orbit of the Moon around the Earth, and eventually reasoned that the influence of gravity must extend over vast distances. After seeing how apples always fall straight to the ground, he spent several years working on the mathematics showing that the force of gravity decreased as the inverse square of the distance.

But what evidence is there that Newton was really inspired by a falling apple? He left no written account suggesting this, although there were other documents suggesting that he had spoken to others about it when he was an old man.

Historians point to the one particular account written by one of Newton's younger contemporaries, an antiquarian and proto-archaeologist called William Stukeley, who also wrote the first biography of Britain's greatest scientist, entitled Memoirs of Sir Isaac Newton's Life.

Stukeley was also born in Lincolnshire, and used this connection to befriend the notoriously cantankerous Newton. Stukeley spent some time in conversation with the older man, and the pair met regularly as fellows of the Royal Society, and talked together. On one particular occasion in 1726, Stukeley and Newton spent the evening dining in London.

"After dinner, the weather being warm, we went into the garden & drank thea under the shade of some apple tree; only he & myself," Stukeley wrote in the meticulously handwritten manuscript released by the Royal Society.

"Amid other discourse, he told me, he was just in the same situation, as when formerly the notion of gravitation came into his mind. Why sh[oul]d that apple always descend perpendicularly to the ground, thought he to himself; occasion'd by the fall of an apple, as he sat in contemplative mood.

"Why sh[oul]d it not go sideways, or upwards? But constantly to the Earth's centre? Assuredly the reason is, that the Earth draws it. There must be a drawing power in matter. And the sum of the drawing power in the matter of the Earth must be in the Earth's centre, not in any side of the Earth.

"Therefore does this apple fall perpendicularly or towards the centre? If matter thus draws matter; it must be proportion of its quantity. Therefore the apple draws the Earth, as well as the Earth draws the apple."

This is the most detailed account of the apple anecdote, but it is not the only one from Newton's day. He had also used it to entertain John Conduitt, the husband of Newton's niece and his assistant at the Royal Mint, which Newton had run in his later years. Conduitt wrote: "In the year 1666 he retired again from Cambridge to his mother in Lincolnshire. Whilst he was pensively meandering in a garden it came into his thought that the power of gravity (which brought an apple from a tree to the ground) was not limited to a certain distance from Earth, but that this power must extend much further than was usually thought.

"Why not as high as the Moon said he to himself & if so, that must influence her motion & perhaps retain her orbit, whereupon he fell a calculating what would be the effect of that supposition."

Both accounts of the apple incident were recalled by Newton some 50 years later. Did it really happen, or was it a story that Newton embellished or even invented?

"Newton cleverly honed this anecdote over time," said Keith Moore, head of archives at the Royal Society. "The story was certainly true, but let's say it got better with the telling." The story of the apple fitted with the idea of an Earth-shaped object being attracted to the Earth. It also had a resonance with the Biblical account of the tree of knowledge, and Newton was known to have extreme religious views, Mr Moore said.

At Woolsthorpe Manor, now owned by the National Trust, the house steward, Margaret Winn, said that the same apple tree, a cooking variety known as Flower of Kent, still grows to the front of the house, in sight of Newton's bedroom window.

"He did tell the story as an old man but you do wonder whether it really happened," said Ms Winn, who has cooked with the apples. But even if the tale was the fanciful imaginings of an old man, the story of the falling apple has gone down in history as the second-greatest "eureka moment" in science, after Archimedes discovered how to work out the volume of objects while he was in the bath.

View the Stukeley manuscript at www.royalsociety.org/turning-the-pages

Eureka moments: How they 'got it'

*Archimedes is thought to have been the first scientist to shout out the Greek word "Eureka!" to mark a breakthrough, when he discovered his principle of buoyancy. Roman writer Vitruvius wrote that Archimedes was taking a bath when he realised that when he stepped into his tub, his body mass displaced a certain weight of water. The scientist is said to have jumped out of the bath and run naked through the streets of Syracuse in Sicily shouting: "Eureka, eureka!" ("I have found it!"). Doubt has since been cast on the authenticity of this story, given that Vitruvius was writing nearly 200 years later.

*Otto Loewi , the German physiologist, spent 17 years trying to come up with definitive proof that nerve impulses were transmitted chemically, and was finally struck by inspiration one night when he had a dream showing him how to carry out a key experiment using a frog's heart. He immediately went to his laboratory to conduct the experiment, noting that electrical stimulation of a frog's vagus nerve released a chemical, now known to be the neurotransmitter acetylcholine, which controlled the heart rate.

*Although it is commonly thought that Charles Darwin came up with his theory of natural selection while on the Galapagos Islands in 1835, he only started to believe in evolution after he returned to England. Instead of being struck by a single "Eureka moment", the scientist spent two decades pondering his observations, finally presenting his controversial theory in his 1859 book On the Origin of Species . Sofia Mitra-Thakur

Join our commenting forum

Join thought-provoking conversations, follow other Independent readers and see their replies

• Utility Menu

Harvard Natural Sciences Lecture Demonstrations

1 Oxford St Cambridge MA 02138 Science Center B-08A (617) 495-5824

• Key to Catalog

enter search criteria into the search box

Newton's apple.

Apple electronically released from platform; fall time given by special circuit and digital display.

What it shows:

How it works:.

A special suspension/release/timing mechanism was designed so that the duration of the fall can be measured to ± 10 µsec. A technique for measuring the distance of the fall to ± 1 mm was also developed. Detailed information has been fully documented and published elsewhere 1 and will not be presented here—only the salient features. The free-fall object can be any material, shape, or size. A few kilograms can be accommodated with the present design. Ideally, it ought to be large enough to assure visibility to everyone in the lecture hall. In the demonstration as originally conceived by David W. Latham, 2 a historical reference to Newton is made by dropping a real apple. The suspension/release/start-timing mechanism is attached to the lecture hall "skyhook," approximately 6 m high. The object to be dropped is suspended by a short length of copper wire. The release of the object is achieved by "instantaneously" vaporizing the suspension wire which is accomplished by discharging a large capacitor through the wire. The vaporization of the wire (the instant of object release) is detected by a simple circuit which provides the "start" pulse for the interval timer. A catching/stop-timing bucket apparatus sits on the floor. Partially filled with wood shavings, it safely catches the falling object at the end of its drop. A photogate fixed to the inside of the bucket provides the "stop" pulse for the interval timer. A collimated light source as well as the power supply for the photodetector and light are also permanent fixtures inside the bucket. The actual distance is measured during the lecture or beforehand. The duration of the free fall is about 1.08 seconds and is displayed on a video monitor. The value of g for Cambridge MA is 9.8038 m/s 2 . Because of the high accuracy obtained in this demonstration experiment, air resistance (the drag coefficient) plays a significant role and the values obtained for g will depend very much on the object that is dropped. For example, a large (7 cm dia.) apple drops with an average g value of 9.657±0.017 m/s 2 while a brass ball (3.8 cm dia.) falls at 9.768±0.002 m/s 2 . These numbers are within the predicted values of the theory when hydrodynamic effects are taken into account.

Setting it up:

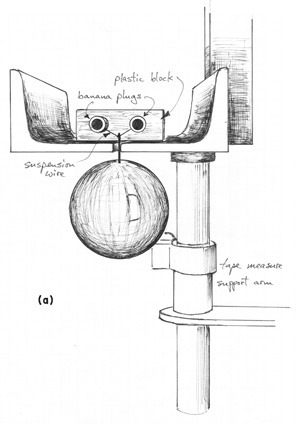
We thought this experiment was good enough to write up and publish. It's pedagogically simple because there are no initial velocities to deal with mathematically. It is quite accurate and gives excellent quantitative results (unless you're bent on measuring the value 9.8038 m/s 2 for g). The humor of the presentation is enhanced by the lecturer eating the apple after the experiment. It does consume an appreciable amount of lecture time (15 to 20 minutes, total) and the lecturer needs to decide whether it's worth it.

1 W. Rueckner and P. Titcomb, Am J Phys 55 , 324 (1987). "An Accurate Determination of the Acceleration of Gravity for Lecture Hall Demonstration". The theory as well as the apparatus is discussed. A reprint of this paper is available in the Prep Room . 2 Smithsonian Astrophysical Observatory, Harvard University. 3 We have been using an HP 5302A universal timer capable of nanosec timing interval resolution. We typically use 100 µsec resolution which most of today's interval timers can easily accommodate. 4 A #8 crochet hook is pushed through the apple and hooks onto the wire. Other objects have the hooks already mounted on them. 5 Stanley 7.5 m - 25 ft tape measure.

Demo Subjects

Newtonian Mechanics Fluid Mechanics Oscillations and Waves Electricity and Magnetism Light and Optics Quantum Physics and Relativity Thermal Physics Condensed Matter Astronomy and Astrophysics Geophysics Chemical Behavior of Matter Mathematical Topics

Key to Catalog Listings

Size : from small [S] (benchtop) to extra large [XL] (most of the hall)  Setup Time : <10 min [t], 10-15 min [t+], >15 min [t++] /span> Rating : from good [★] to wow! [★★★★] or not rated [—] 

Complete key to listings